Aufgaben zur Tangente
- 1
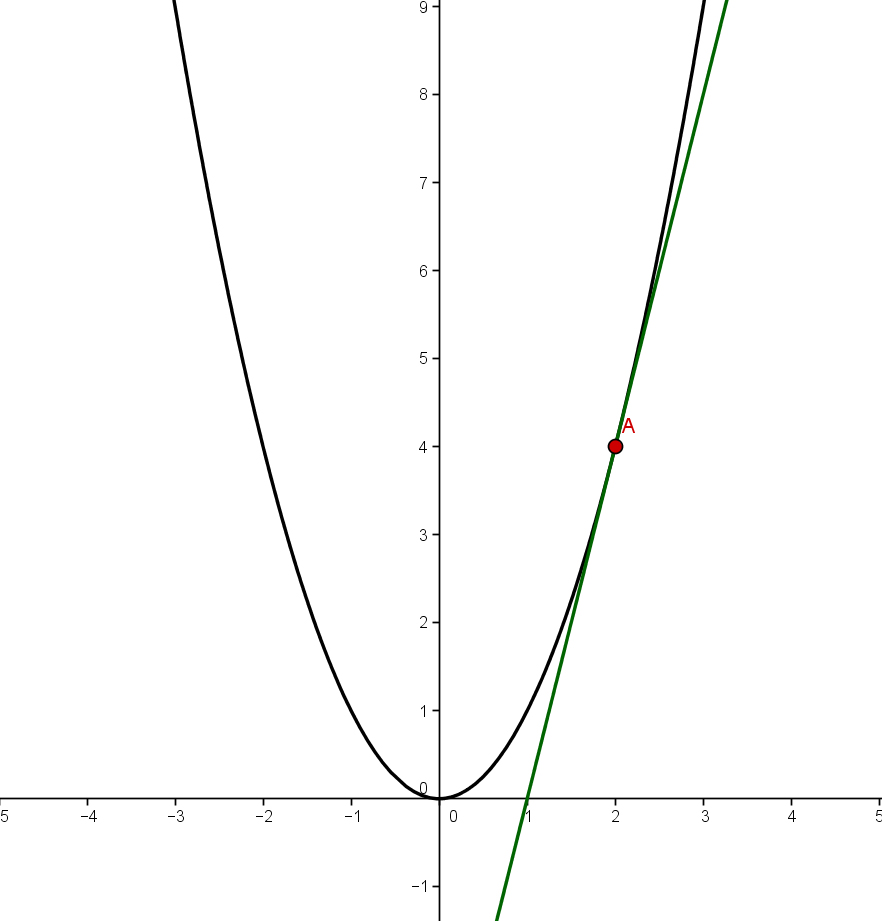
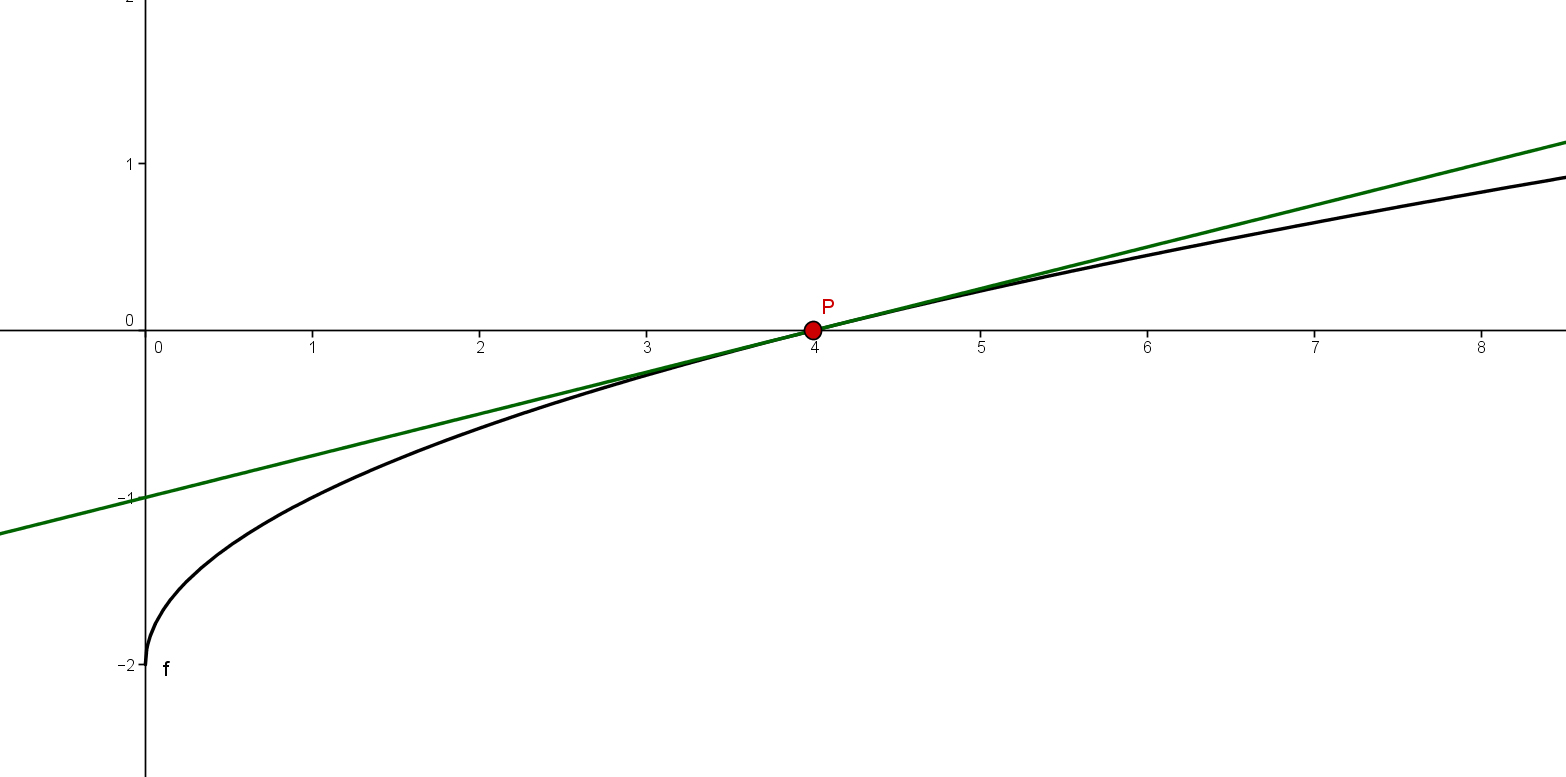
Gegeben ist die Funktion .
Stelle die Gleichung der Tangente im Punkt auf.
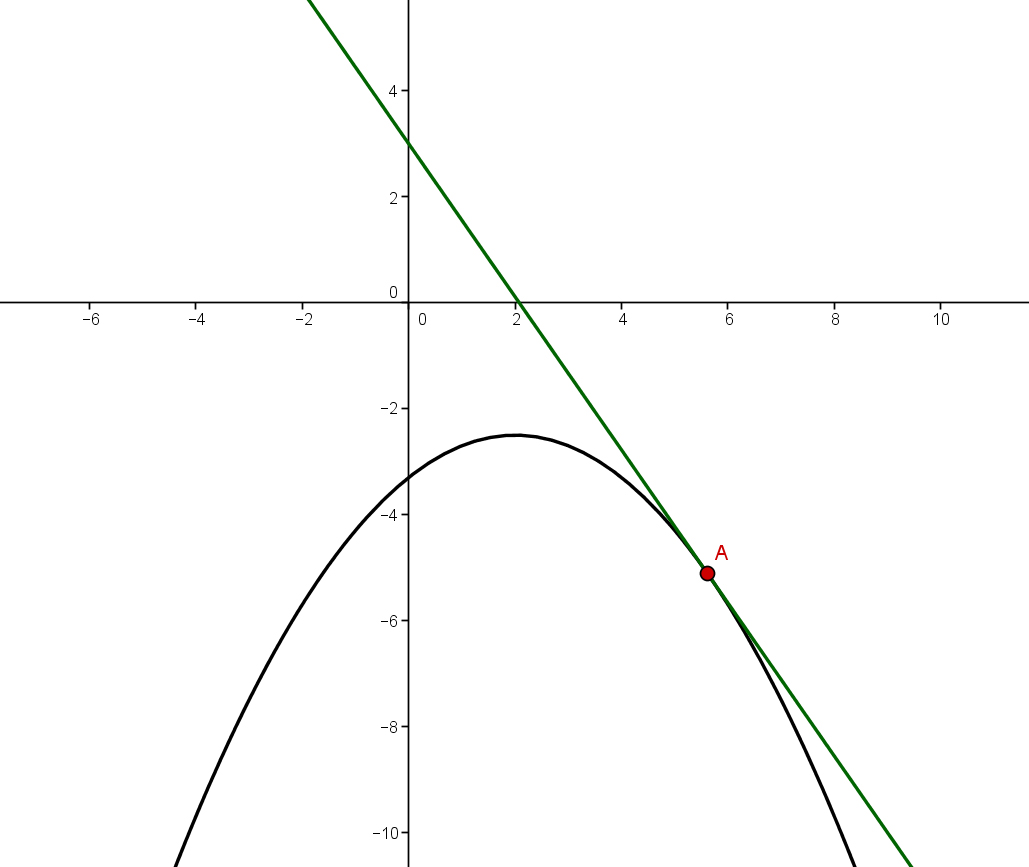
- 2
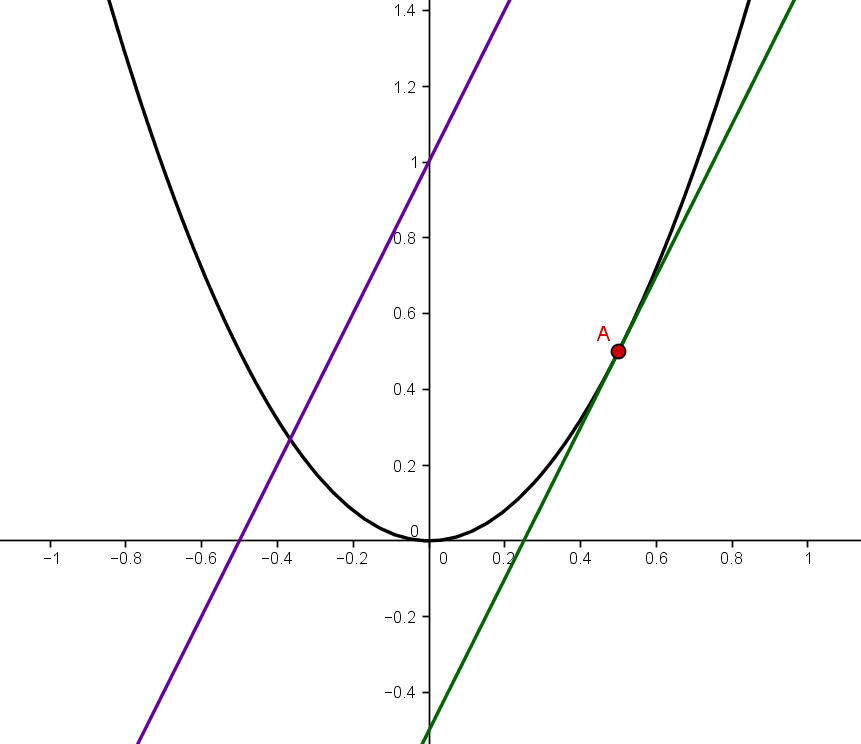
Bestimme die Gleichung der Tangente an den Graphen der Funktion , wobei die Tangente parallel zur Geraden verlaufen soll.
- 3
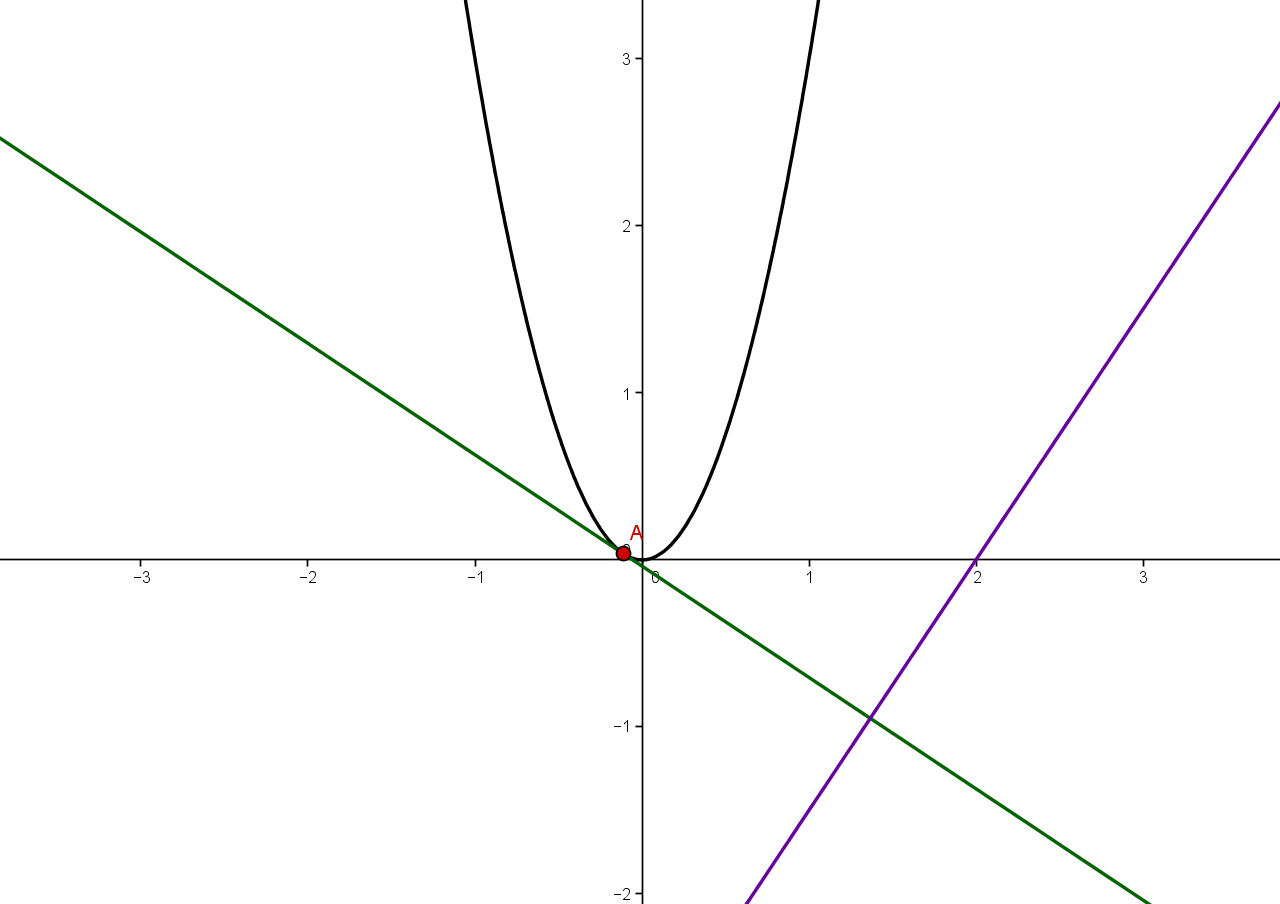
Bestimme die Gleichung der Tangente an die Funktion , die senkrecht zur Geraden ist.
- 4
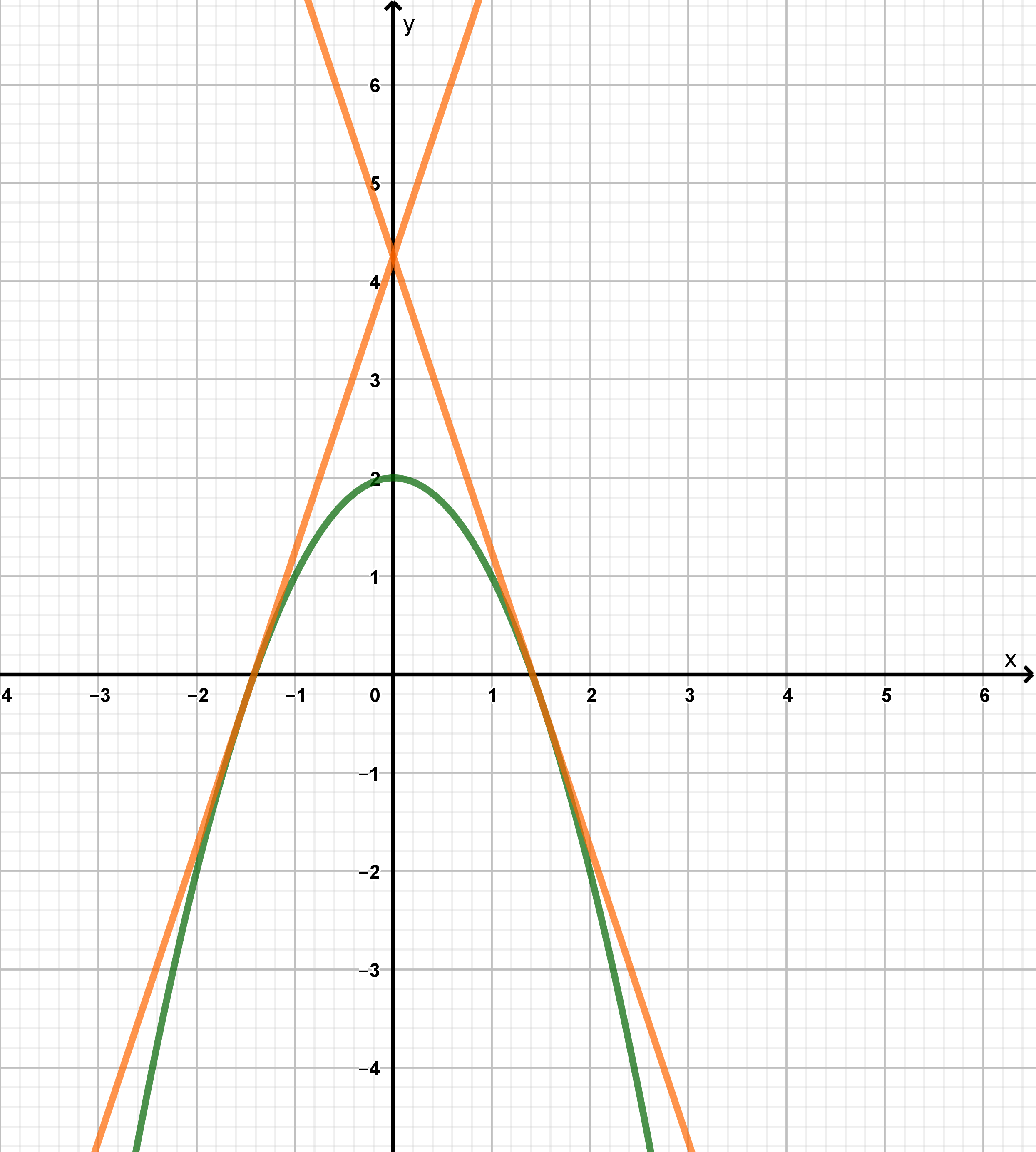
Bestimme die Tangenten an die Funktion , die sich im Punkt schneiden.
- 5
Bestimme die Gleichung der Tangente an die Funktion durch den Punkt .
- 6
An die Funktion soll vom Punkt aus eine Tangente mit negativer Steigung gelegt werden. Bestimme die Gleichung der Tangente und den Berührpunkt.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?