Gemischte Aufgaben zu trigonometrischen Funktionen

1
Berechne ohne Taschenrechner:
$\sin (\cos (\frac{π}{2})) + \tan (1 - \sin (\frac{5 π}{2}))$
Für diese Aufgabe benötigst Du folgendes Grundwissen: trigonometrische Funktionen
Berechne $\sin (\frac{5 π}{2})$ . Die Sinusfunktion ist periodisch mit Periode $2 π$ .
$\sin (\cos (\frac{π}{2})) + \tan (1 - \sin (\frac{5 π}{2}))$
$= \sin (\cos (\frac{π}{2})) + \tan (1 - \sin (\frac{π}{2} + 2 π))$
$= \sin (\cos (\frac{π}{2})) + \tan (1 - \sin (\frac{π}{2}))$
Berechne $\cos (\frac{π}{2})$ und $\sin (\frac{π}{2})$ .Die Werte von $\sin (\frac{π}{2})$ und $\cos (\frac{π}{2})$ kannst du dir leicht merken. Deswegen brauchst du dafür keinen Taschenrechner.Als Hilfe kannst du dir den Graphen zu den Funktionen anschauen.
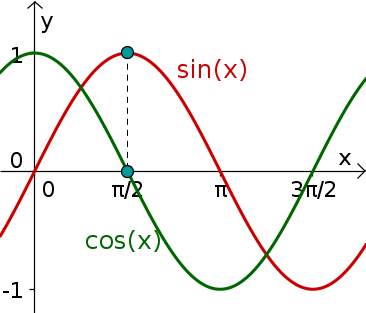
Daraus kannst du ablesen:
$\cos (\frac{π}{2}) = 0$
$\sin (\frac{π}{2}) = 1$
Diese Werte setzt du in den Term ein.
$. . . = \sin (\cos (\frac{π}{2})) + \tan (1 - \sin (\frac{π}{2}))$
$= \sin (0) + \tan (1 - 1)$
$= \sin (0) + \tan (0)$
Benutze nun die Definition der Tangensfunktion: $\tan (x) = \frac{\sin (x)}{\cos (x)}$ .
$. . . = \sin (0) + \tan (0)$
$= \sin (0) + \frac{\sin (0)}{\cos (0)}$
Setze die Funktionswerte ein. Zur Hilfe kannst du wieder den Graphen betrachten.
$. . . = \sin (0) + \frac{\sin (0)}{\cos (0)} = 0 + \frac{0}{1} = 0$
Also:
$\sin (\cos (\frac{π}{2})) + \tan (1 - \sin (\frac{5 π}{2})) = . . . = 0$

Berechne den Winkel $α$ im Intervall $[0, π]$ . Gib dein Ergebnis im Gradmaß an:

1 + 3 \cdot \sin^{2} (α) = 1 + \cos^{2} (α)

3
Es ist $\cos (2) \approx - 0,42$ . Bestimme 3 weitere Winkel, die den gleichen Kosinuswert haben.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Periode einer Funktion
Gegeben: $\cos (2) \approx - 0,42$
Gesucht: Weitere Stellen $a, b, c$ mit $\cos (a) = \cos (b) = \cos (c) = \cos (2)$
Zeichne die Kosinusfunktion, um die Periode zu bestimmen.
Betrachtet man den Graphen der Kosinusfunktion, so erkennt man, dass sich der Kosinus alle $2 π$ wiederholt. Das heißt, Kosinus hat die Periode $2 π$ .
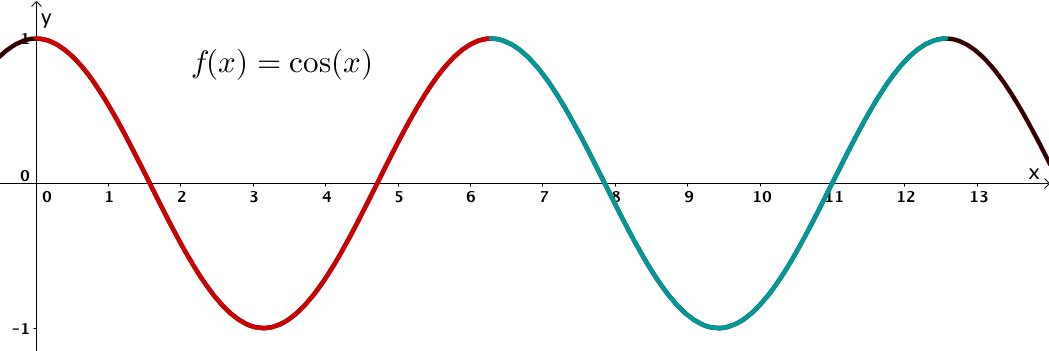
Da der Kosinus Periode $2 π$ hat, gilt allgemein
$\cos (x) = \cos (x + 2 π) = \cos (x + 4 π) = \dots$
für jede Stelle $x$ und damit
$\cos (2) = \cos (2 + 2 π) = \cos (2 + 4 π) = \dots$
Daher findet man weitere Stellen $a, b, c$ zum Beispiel mit
$a = 2 + 2 π, b = 2 + 4 π, c = 2 + 6 π$
Alternative Lösung
Jetzt beschreiben wir eine andere Möglichkeit, wie du die Aufgabe lösen kannst.
Hierfür benötigst Du zusätzlich folgendes Grundwissen:
Kosinus ist eine gerade Funktion
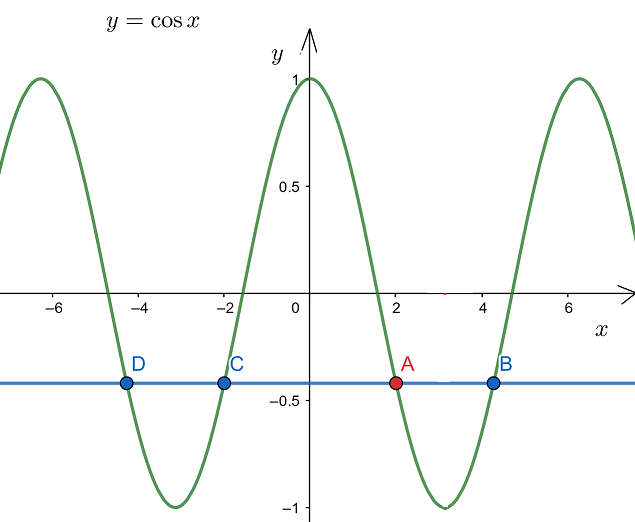
Bisher haben wir den Punkt $A$ mit den Koordinaten $(2, \cos (2))$ .
Wir wissen, dass $\cos (x - 2 π) = \cos (x)$ ist.
Daher können wir $a = 2 - 2 π$ nehmen, da der Kosinus dort denselben Wert hat (Punkt $D$ ).
Wie man in der Skizze sieht, ist der Graph der Kosinusfunktion achsensymmetrisch zur $y$ -Achse. Daher erhalten wir die Punkte $C$ als Spiegelpunkt zu $A$ mit $b = - 2$ und $B$ als Spiegelpunkt zu $D$ mit $c = 2 π - 2$ als weitere Lösungen.
4
Prüfe, ob folgende Gleichungen für jede Stelle $x$ gelten:
1. $\sin (x) + \sin (y) = \sin (x + y)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus- und Kosinusfunktion
  Prüfe: $\sin (x + y) = \sin (x) + \sin (y)$
  Betrachte den Graphen der Sinusfunktion und prüfe die Werte von $\sin (x + y)$ und $\sin (x) + \sin (y)$ an beispielsweise $x = y = \frac{π}{2}$ . Beachte, dass die Gleichung nicht mehr erfüllt ist, wenn die Gleichung an einem expliziten Punkt nicht gilt.
  $\sin (\frac{π}{2}) = 1$ und
  $\sin (\frac{π}{2} + \frac{π}{2}) = \sin (π) = 0$
  Damit ist $\sin (\frac{π}{2} + \frac{π}{2}) \neq \sin (\frac{π}{2}) + \sin (\frac{π}{2})$
  Und daher im Allgemeinen: $\sin (x + y) \neq \sin (x) + \sin (y)$
  Beachte, dass es durchaus Stellen $x, y$ gibt, welche die Gleichung erfüllen. Zum Beispiel $x = y = 0$ , denn es ist $\sin (0) = 0$ . Es war jedoch nach der allgemeinen Gültigkeit der Gleichung gefragt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $\cos (x) + \cos (y) = \cos (x + y)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus- und Kosinusfunktion
  Prüfe: $\cos (x) + \cos (y) = \cos (x + y)$
  Betrachte den Graphen der Sinusfunktion und prüfe die Werte von $\cos (x + y)$ und $\cos (x) + \cos (y)$ an beispielsweise $x = y = 0$ . Beachte, dass die Gleichung nicht mehr erfüllt ist, wenn die Gleichung an einem expliziten Punkt nicht gilt.
  $\cos (0) + \cos (0) = 2$
  $\cos (0 + 0) = \cos (0) = 1$
  Damit ist allgemein $\cos (x) + \cos (y) \neq \cos (x + y) .$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5
Finde Beispiele für Phänomene in der Realität, die sich durch Sinus- und Kosinusfunktionen beschreiben lassen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinusfunktion und Kosinusfunktion
Im allgemeinen lassen sich Wellen durch Sinus- und Kosinusfunktionen beschreiben. Das können zum Beispiel Wasserwellen, Schallwellen, Elektromagnetische Wellen sein. Das heißt, dass diese Funktionen vorallem in der Physik ihre Anwendung finden.
6
Prüfe, für welche $x$ im Intervall zwischen $0$ und $2 π$ die folgenden Gleichungen gelten:
Hinweis: Verwende den trigonometrischen Pythagoras $\sin^{2} (x) + \cos^{2} (x) = 1$ .
1. $\sin^{2} (x) - \cos^{2} (x) = 1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinusfunktion und Kosinusfunktion
  Gegeben:
  $\sin^{2} (x) - \cos^{2} (x) = 1$
  Verwende den trigonometrischen Pythagoras wie im Hinweis.
  $\sin^{2} (x) - \cos^{2} (x) = \sin^{2} (x) + \cos^{2} (x)$
  Subtrahiere auf beiden Seiten $\sin^{2} (x)$ und addiere auf beiden Seiten $\cos^{2} (x)$ .
  $2 \cdot \cos^{2} (x) = 0$
  Teile durch $2$ und ziehe die Wurzel.
  $\cos (x) = 0$
  Lese aus dem Graphen der Kosinusfunktion ab, welche Nullstellen der Kosinus zwischen $0$ und $2 π$ hat.
  $x = \frac{π}{2}$ oder $x = \frac{3 π}{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $(1 - \cos (x)) (1 + \cos (x)) = \sin (x)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinusfunktion und Kosinusfunktion
  $(1 - \cos (x)) (1 + \cos (x)) = \sin (x)$
  Verwende auf der linken Seite der Gleichung die dritte binomische Formel.
  $1 - \cos^{2} (x) = \sin (x)$
  Verwende den trigonometrischen Pythagoras.
  $\sin^{2} (x) = \sin (x)$
  Bringe $\sin (x)$ auf die andere Seite und klammere dann $\sin (x)$ aus.
  $\sin (x) (\sin (x) - 1) = 0$
  Diese Gleichung ist erfüllt, falls $\sin (x) = 0$ oder $\sin (x) - 1 = 0$ .
  $\sin (x) = 0$ , falls $x = 0$ oder $x = π$ oder $x = 2 π$
  $\sin (x) = 1$ , falls $x = \frac{π}{2}$
  Gebe die Lösungen in einer Lösungsmenge an.
  $L = {0, \frac{π}{2}, π, 2 π}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $(1 + \sin (x)) (1 - \sin (x)) = \cos^{2} (x)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinusfunktion und Kosinusfunktion
  $(1 - \sin (x)) (1 + \sin (x)) = \cos^{2} (x)$
  Verwende die dritte binomische Formel auf der linken Seite der Gleichung.
  $1 - \sin^{2} (x) = \cos^{2} (x)$
  Addiere auf beiden Seiten der Gleichungen $\sin^{2} (x)$ .
  $1 = \sin^{2} (x) + \cos^{2} (x)$
  Bemerke, dass dies genau der trigonometrische Pythagoras ist, welche für jede Stelle $x$ erfüllt ist.
  $x \in [0,2 π]$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $\cos^{2} (x) + \sin^{2} (x) = 2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinusfunktion und Kosinusfunktion
  Gegeben:
  $\cos^{2} (x) + \sin^{2} (x) = 2$
  Verwende den trigonometrischen Pythagoras: $\sin^{2} (x) + \cos^{2} (x) = 2$
  Vergleichst du diese Formel mit der Augangsgleichung, erhälst du den Ausdruck " $1 = 2$ ", welcher jedoch nie erfüllt ist.
  Lösungsmenge $L = {}$
  Sprechweise: "Die Lösungsmenge ist leer." bzw. "Es existiert keine Lösung."
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7
Entscheide, ob die folgenden Beziehungen zwischen den trigonometrischen Funktionen richtig oder falsch sind.
1. $\cos (90 ° - α) = \sin (α)$
  Richtig
  Falsch
2. $\sin (α + 180 °) = - \sin (α)$
  Richtig
  Falsch
8
Vereinfache den folgenden Term, bis nur noch $\tan (x)$ darin vorkommt:
$(1 - \frac{1}{\cos (x)}) (1 + \frac{1}{\cos (x)})$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangensfunktion
Forme $(1 - \frac{1}{\cos (x)}) (1 + \frac{1}{\cos (x)})$ um.
Verwende die dritte binomische Formel.
$= 1 - \frac{1}{\cos^{2} (x)}$
Bilde den Hauptnenner und führe die Brüche zusammen.
$= \frac{\cos^{2} (x) - 1}{\cos^{2} (x)}$
Verwende den trigonometrischen Pythagoras.
$= - \frac{\sin^{2} (x)}{\cos^{2} (x)}$
Verwende die Definition des Tangens.
$= - (\tan (x))^{2}$

Löse für $x \in] - \frac{π}{2}, \frac{π}{2} [$ die folgende Gleichung nach $x$ auf:

\tan (x) + \sin (x) = 0

Löse für $x \in] \frac{π}{2}, \frac{3 π}{2} [$ die folgende Gleichung nach $x$ auf:

$(\tan (x))^{3} + 2 \tan (x) = \frac{\sin (x)}{\cos^{3} (x)}$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$1 + 3 \cdot \cos^{2} (α)$	$=$	$1 + \sin^{2} (α)$	$- \sin^{2} (α)$
	↓	Bringe Sinus und Kosinus auf eine Seite.
$1 + 3 \cdot \cos^{2} (α) - \sin^{2} (α)$	$=$	$1$
	↓	Nach Betrachten des Terms, entdeckst du, dass du den trigonometrischen Pythagoras anwenden kannst.
$1 - \sin^{2} (α) + 3 \cdot \cos^{2} (α)$	$=$	$1$
	↓	Wende den trigonometrischen Pythagoras an.
$\cos^{2} (α) + 3 \cdot \cos^{2} (α)$	$=$	$1$
$4 \cdot \cos^{2} (α)$	$=$	$1$	$: 4$
$\cos^{2} (α)$	$=$	$\frac{1}{4}$	$\sqrt{}$
	↓	Ziehe die Wurzel.
$\cos (α)$	$=$	$\sqrt{\frac{1}{4}}$
$\cos (α)$	$=$	$\pm \frac{1}{2}$

$\tan (x) + \sin {(x)}^{}$	$=$	$0$
	↓	Verwende die Definition des Tangens.
$\frac{\sin (x)}{\cos (x)} + \sin (x)$	$=$	$0$
	↓	Klammere sin(x) aus.
$\sin (x) (\frac{1}{\cos (x)} + 1)$	$=$	$0$
	↓	Das Produkt ist $0$ , falls einer der beiden Faktoren $0$ ist.
$\sin (x)$	$=$	$0$
	↓	oder
$\frac{1}{\cos (x)} + 1$	$=$	$0$
	↓	Forme die zweite Gleichung um, indem du beiden Seiten mit $- 1$ subtrahierst und mit $\cos (x)$ multiplizierst.
$\sin (x)$	$=$	$0$
	↓	oder
$- \cos (x)$	$=$	$1$
	↓	Multipliziere auf beiden Seiten der zweiten Gleichung mit $(- 1)$ .
$\sin (x)$	$=$	$0$
	↓	oder
$\cos (x)$	$=$	$- 1$
	↓	Betrachte die Graphen der Sinus- und Kosinusfunktion zur Bestimmung der $x$ -Werte in dem vorgeschriebenen Intervall.
$x$	$=$	$0$

$(\tan (x))^{3} + 2 \tan (x)$	$=$	$\frac{\sin (x)}{\cos^{3} (x)}$
	↓	Verwende, dass $\frac{\sin (x)}{\cos^{3} (x)} = \frac{\tan (x)}{\cos^{2} (x)}$ und subtrahiere auf beiden Seiten mit diesem Term.
$(\tan (x))^{3} + 2 \tan (x) - \frac{\tan (x)}{\cos^{2} (x)}$	$=$	$0$
	↓	Klammere $\tan (x)$ aus.
$\tan (x) (\tan (x)^{2} + 2 - \frac{1}{\cos^{2} (x)})$	$=$	$0$
	↓	Verwende, dass $\tan (x)^{2} = \frac{\sin^{2} (x)}{\cos^{2} (x)}$ .
$\tan (x) (\frac{\sin^{2} (x)}{\cos^{2} (x)} + 2 - \frac{1}{\cos^{2} (x)})$	$=$	$0$
	↓	Bringe den Term in der Klammer auf einen Hauptnenner.
$\tan (x) (\frac{\sin^{2} (x) + 2 \cos^{2} (x) - 1}{\cos^{2} (x)})$	$=$	$0$
	↓	Verwende den trigonometrischen Pythagoras und schreibe die $1$ um.
$\tan (x) (\frac{\sin^{2} (x) + 2 \cos^{2} (x) - \sin^{2} x - \cos^{2} x}{\cos^{2} (x)})$	$=$	$0$
	↓	Fasse den Zähler zusammen.
$\tan (x) (\frac{\cos^{2} (x)}{\cos^{2} (x)})$	$=$	$0$
	↓	Kürze.
$\tan (x) \cdot 1$	$=$	$0$
$\tan (x)$	$=$	$0$

Gemischte Aufgaben zu trigonometrischen Funktionen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?