1 Übersicht
In diesem Kurs geht es um Bruchgleichungen und Strategien, wie du diese lösen kannst.
Dauer: ca. h
Vorwissen:
Hauptnenner bilden
Rechnen mit Bruchtermen

Du lernst:
Definition einer Bruchgleichung
Bestimmung der Definitionsmenge
Lösen einer Bruchgleichung (mithilfe der Hauptnenner-und Über-Kreuz-Methode)
Graphische Darstellung von Bruchgleichungen
2 Ollis Hoverboard (1/2)
Aufgabe:
Olli hat zu seinem Geburtstag ein nagelneues Hoverboard bekommen und will dieses austesten.
Olli fährt zum Bäcker und braucht dafür . Jetzt will Olli wissen, wie lange er zu seinem Freund Charlie bräuchte. Charlie wohnt von Olli entfernt. Er fragt seine große Schwester Leonie.

3 Ollis Hoverboard 2/2
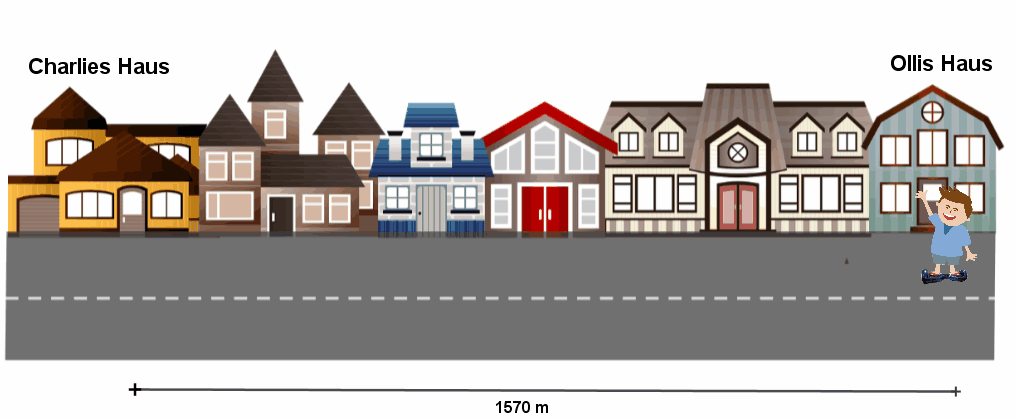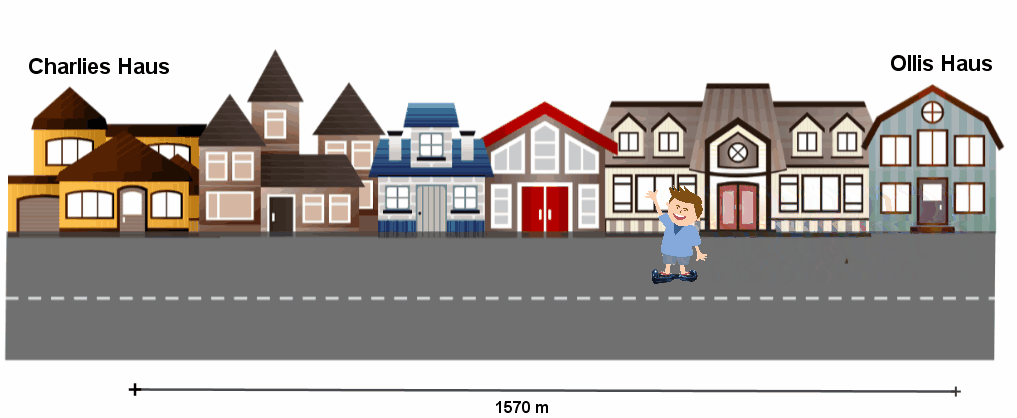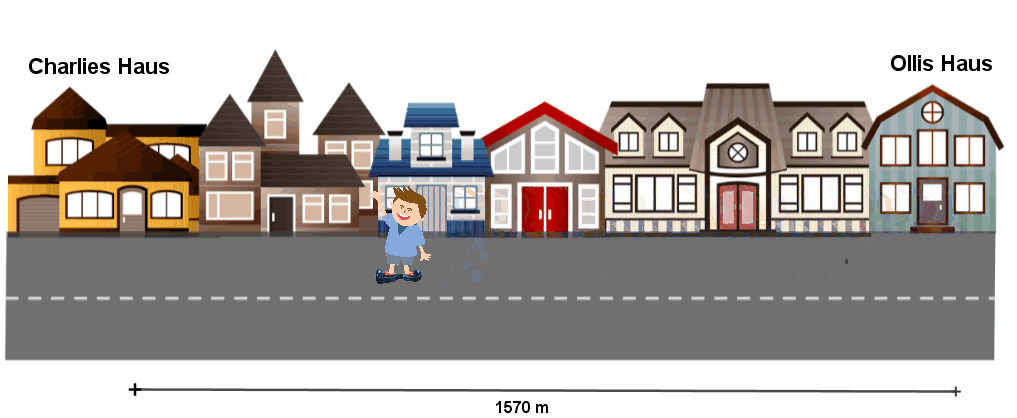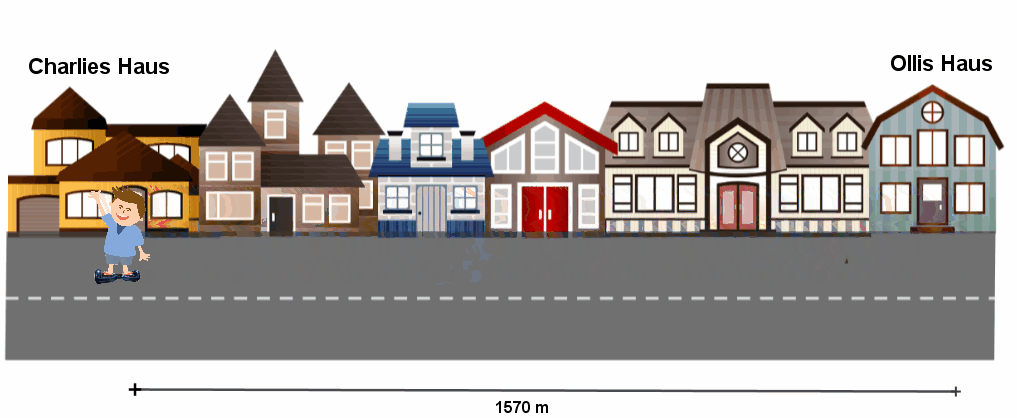
Olli fährt mit der gleichen mittleren Geschwindigkeit zu Charlie, mit der er zum Bäcker fährt. Berechne zuerst Ollis mittlere Geschwindigkeit. Du rechnest den Weg geteilt durch die Zeit:
Jetzt kannst du eine Gleichung aufstellen, um auf die gesuchte Zeit zu kommen. Die Geschwindigkeit muss wieder sein, da Olli zu Charlie genauso schnell fährt wie zum Bäcker.
Der Weg ist diesmal die Strecke von Olli zu Charlie, also . Die Zeit ist die unbekannte Größe .
Jetzt musst du die Gleichung nach auflösen.
Dazu müsstest du eine Bruchgleichung lösen. Du fragst dich, wie das geht? Dies wird dir im Folgenden erklärt.
4 Definition Bruchgleichung
3 Eigenschaften einer Bruchgleichung:
1. Es ist eine Gleichung,
2. in der ein oder mehrere Brüche stehen,
3. bei denen die gesuchte Variable in mindestens einem Nenner vorkommt.

5 Beispiele zu Bruchgleichungen
Beispiele:
Was ist eine Bruchgleichung und was nicht?

Das ist eine Bruchgleichung, da hier die Eigenschaften , und erfüllt sind.

Das ist auch eine Bruchgleichung, da hier ebenfalls die Eigenschaften , und erfüllt sind.

Das ist keine Bruchgleichung. Eigenschaften , sind erfüllt, aber kein Bruch hat eine Variable im Nenner.

Das ist keine Bruchgleichung. Das ist keine Gleichung, sondern nur ein Term. Also ist Eigenschaft verletzt.
6 Übungsaufgaben zur Definition von Bruchgleichungen
Laden
7 Definitionsmenge einer Bruchgleichung (1/2)
Du hast schon gelernt, dass du nicht durch teilen darfst. Finde die Zahlen für , mit denen der Nenner wird. Schließe sie aus der Definitionsmenge aus. Diese Zahlen nennt man Definitionslücken.
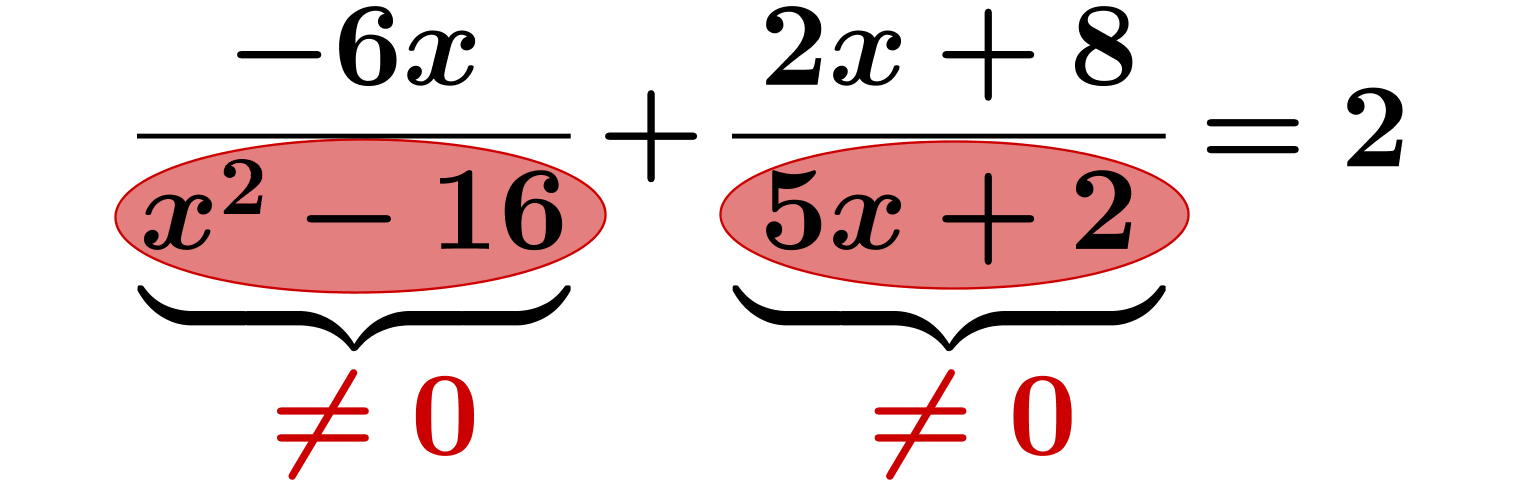
Beispiel einer Bruchgleichung: Der Nenner darf nicht 0 sein.
Die Definitionsmenge einer Bruchgleichung besteht aus allen Zahlen, die du für die Variable einsetzen darfst.
Schreibweise
Untern rechts kannst du weiterklicken, um zu lernen, wie man die Definitionsmenge richtig aufschreibt.
Beispiel:
Wenn eine Bruchgleichung ihre Definitionslücken bei und hat, schreibst du:
8 Bestimmung der Definitionsmenge (2/2)
Hier lernst du, wie du vorgehen musst, um die Definitionsmenge herauszufinden.
Für jeden Bruch, der eine Variable im Nenner hat, machst du Folgendes:
Nenner herausschreiben
Setze Nenner gleich
Löse nach der Variablen auf
Nun hast du die Definitionslücken gefunden und kannst diese aus der Definitionsmenge ausschließen.
Beispiel
Ersten Nenner gleich setzen und nach der Variablen auflösen.
Zweiten Nenner gleich setzen und nach der Variablen auflösen.
9 Übungsaufgaben zur Bestimmung der Definitionsmenge
Laden
10 Bruchgleichungen lösen

Jetzt hast du das Problem, dass du die Unbekannte im Nenner hast. Dein Ziel ist es, diese aus dem Nenner zu entfernen. Es gibt Umformungen, mit welchen du es schaffst, eine bruchtermfreie Gleichung zu erhalten. Sobald keine Bruchterme mehr vorhanden sind, kannst du die Gleichung wie gewohnt lösen. Im Folgenden lernst du zwei wichtige Verfahren kennen, um Bruchgleichungen zu lösen:
11 Hauptnenner-Methode (1/3)
Jetzt lernst du die eine Methode zur Lösung von Bruchgleichungen kennen, die du immer einsetzen kannst. Hier geht es darum, den Hauptnenner zu bilden.
Der Hauptnenner ist das kleinste gemeinsame Vielfache der Nenner. Du kannst bereits Brüche auf einen gemeinsamen Hauptnenner bringen und anschließend addieren. Das gleiche Verfahren benutzen wir nun zum Lösen von Bruchgleichungen.
Hauptnenner finden:
Suche nach einzelnen Faktoren der Nenner.
Diese können als Bausteine bezeichnet werden. (Im Bild sind diese in verschiedenen Farben markiert.)
Multipliziere alle Bausteine miteinander.
Achtung: Verwende hierbei die Bausteine, die in mehreren Nennern vorkommen, nur einmal.
Dies ist nun dein Hauptnenner!
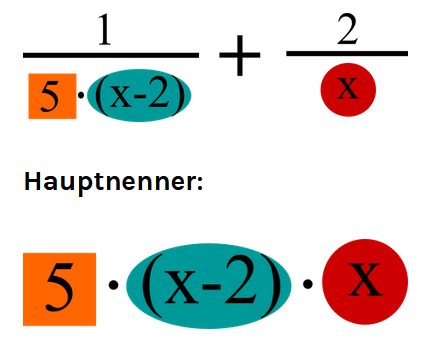
Um den Hauptnenner bei Bruchgleichungen zu bestimmen, musst du alle Nenner links und rechts von dem Gleichheitszeichen beachten!
Vorgehensweise
Beispiel:
Suche die einzelnen Faktoren der Nenner:
Die Farben markieren die einzelnen Faktoren. Doppelte Faktoren müssen als Baustein nur einmal aufgeführt werden.
Die Bausteine sind:
12 Hauptnenner-Methode (2/3)
Die Abbildung (rechts) zeigt das Schema zur Lösung von Bruchgleichungen mithilfe des Hauptnenners. Den Hauptnenner kannst du seit der letzten Folie bilden. Nun musst du alle Brüche auf den Hauptnenner erweitern.
Betrachte nochmals das Beispiel von vorher:
Der Hauptnenner besteht aus den Bausteinen , und .
Hauptnenner:
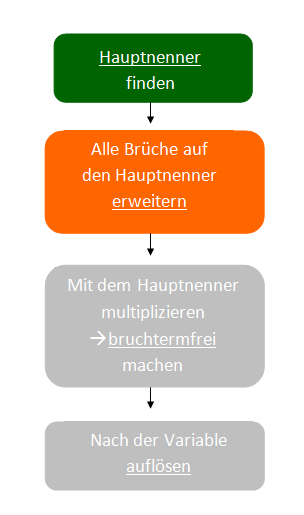
Nun musst du alle Brüche auf den Hauptnenner erweitern!
Jeder Bruch muss im Nenner jeden Baustein enthalten.
Betrachten wir die Brüche einzeln:
1. Bruch:
Ermittle, welche Bausteine des Hauptnenners im Nenner des Bruchs fehlen (die Farben helfen dir dabei). Es fehlt der Baustein: Erweitere mit diesem, indem du den Nenner und den Zähler mit multiplizierst.
Jetzt hat der Bruch den Hauptnenner als Nenner.
2. Bruch
Hier fehlt der Baustein: . Erweitere mit diesem.
13 Hauptnenner-Methode (3/3)
Die ersten zwei Schritte der Abbildung (rechts) hast du schon erledigt. Komme nun zum dritten.
Erinnere dich erneut an die Gleichung:
Jetzt musst du deine Gleichung bruchtermfrei machen.
Multipliziere hierfür beide Seiten mit dem Hauptnenner. Damit fällt der Nenner ganz weg.
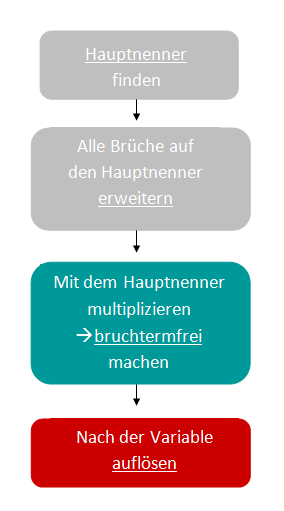
Du erhältst:
Jetzt kannst du die Gleichung wie gewohnt lösen.
| ↓ | Multipliziere die Klammer aus. | ||
| ↓ | Subtrahiere . | ||
| ↓ | Teile durch . | ||
14 Beispiel zu Hauptnenner-Methode (1/3)

Nun betrachten wir ein etwas längeres Beispiel.
mit .
Löse die Bruchgleichung mit der Hauptnenner-Methode!
Finden des Hauptnenners
Finde den gemeinsamen Hauptnenner. Zunächst suchst du die einzelnen Faktoren der Nenner.
Du kannst folgende Faktoren ablesen:
Du siehst, dass sowohl im ersten als auch im zweiten Aufzählungspunkt steht. Du verwendest somit für den gemeinsamen Hauptnenner nur die Bausteine:
und .
Bausteine:
Multipliziere die Bausteine für den Hauptnenner.
Deshalb erhältst du als Hauptnenner: .
15 Beispiel zu Hauptnenner-Methode (2/3)

Erweitern zum Hauptnenner
Erweitere alle Brüche zum Hauptnenner.
1. Bruch
Erweitere mit den Bausteinen und .
2. Bruch
Erweitere mit dem Baustein .
3. Bruch
Erweitere mit den Bausteinen und .
Du erhältst:
16 Beispiel zu Hauptnenner-Methode (3/3)

Bruchtermfreie Gleichung
Multipliziere beide Seiten mit dem Hauptnenner. Somit fällt der Nenner weg. Anschließend kannst du nach auflösen.
| ↓ | Multipliziere die beiden Klammern aus. | ||
| ↓ | Subtrahiere von beiden Seiten. | ||
| ↓ | Vereinfache und bringe die Zahl auf die andere Seite. | ||
| ↓ | Teile durch . | ||
Lösung
liegt in dem Definitionsbereich der Gleichung. Also ist die Lösungsmenge .
17 Übungsaufgaben zu Hauptnenner-Methode
Laden
18 Über-Kreuz-Multiplizieren (1/2)
Das Über-Kreuz-Multiplizieren folgt aus der Hauptnennermethode. Bei bestimmten Bruchgleichungen spart man sich mit dieser Methode die Suche nach dem Hauptnenner.
Sie bietet sich für Bruchgleichungen an, bei denen links und rechts vom =-Zeichen jeweils nur ein Bruchterm steht. Diese Lösungsmöglichkeit wird dir nun genauer erklärt.
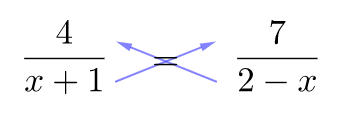
Herleitung
Du hast eine Bruchgleichung der Form:
Allgemeines | Beschreibung | Beispiel |
|---|---|---|
Zunächst multipliziere beide Seiten der Gleichung mit dem Produkt aus beiden Nennern. | ||
Nun kannst du in beiden Brüchen kürzen. | ||
Du bist am Ziel: Nun hast du eine bruchtermfreie Gleichung. Diese kannst du wie gewohnt lösen :) |
19 Über-Kreuz-Multiplizieren (2/2)
Vorsicht!
Bei diesem Verfahren musst du einige Dinge beachten:
Auf beiden Seiten der Gleichung muss genau ein Bruch stehen.
Kürze beide Brüche so weit wie möglich, bevor du multiplizierst.
Beachte, dass du gegebenenfalls Klammern setzen musst.
Beispiel:
Laden
20 Übungsaufgaben zu Über-Kreuz-multiplizieren
Laden
21 Lösung Motivation
Zu Beginn des Kurses konntest du das Problem noch nicht lösen. Jetzt kennst du zwei Methoden zum Lösen von Bruchgleichungen. Hier kannst du beide verwenden. Entscheide dich für eine und löse folgende Bruchgleichung:
Der Übersicht halber werden die Einheiten in den nächsten Schritten weggelassen.

Über-Kreuz-Multiplizieren:
| ↓ | Schreibe als Bruch. | ||
| ↓ | Multipliziere über Kreuz! | ||
| ↓ | Vereinfache. | ||
| ↓ | Teile durch . | ||
Olli braucht also bis zu Charlie.
Hauptnenner-Methode:
| ↓ | Du kannst vielleicht erkennen, dass der einzige Faktor ist. Somit ist der Hauptnenner . Erweitere zum Hauptnenner. | ||
| ↓ | Multipliziere mit dem Hauptnenner. Damit fallen die Nenner weg. | ||
| ↓ | Teile durch . | ||
Olli braucht also zu Charlie.
22 Bruchgleichungen graphisch (1/2)

Betrachte die Terme rechts und links von dem Gleichheitszeichen als Funktionsterme von zwei verschiedenen Funktionen. Jetzt kannst du die Graphen der Funktionen aufzeichnen. Die Lösung der Gleichung ist dann die -Koordinate des Schnittpunkts der zwei Graphen.
Beispiel
Schaue dir folgende Bruchgleichung an:
Setze:
und .
In der nebenstehenden Grafik kannst du die Funktionsgraphen betrachten, indem du auf die Buttons klickst.
Kannst du selber schon erkennen, an welcher Stelle die Definitionslücken der Funktionen sind, und was die Lösung der Gleichung ist?
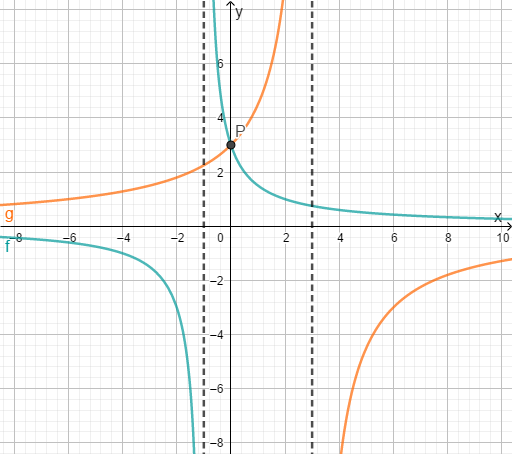
23 Bruchgleichungen graphisch (2/2)
Definitionslücken
Die Definitionslücken einer Funktion sind im Graphen besonders gut als senkrechte Asymptoten erkennbar. Hier zeigen die gestrichelten Linien in der Grafik die senkrechten Asymptoten, also die Stellen an denen bzw. nicht definiert sind.
In dem Fall rechts gibt es zwei Asymptoten, nämlich bei der und bei der .
An diesen Stellen sind die Nenner der Funktionsterme gleich . Alle anderen Werte können wir einsetzen. Für die Definitionsmenge von und für die Definitionsmenge von gilt also:
Also ist die Definitionsmenge der Gleichung .
Lösung der Gleichung
Gesucht ist die Lösung von mit
und .
Bestimmst du den Schnittpunkt der Graphen, erhältst du auch gleichzeitig die Lösung der Gleichung.
An den Graphen von oben kannst du den Schnittpunkt bestimmen, dieser liegt bei . Es liegen keine weiteren Schnittpunkte vor.
Lies nun die -Koordinate von dem Schnittpunkt ab, diese ist die Lösung der Gleichung. Bei dem Beispiel ist die -Koordinate von . ist in der Definitionsmenge enthalten und somit tatsächlich eine Lösung der Gleichung.
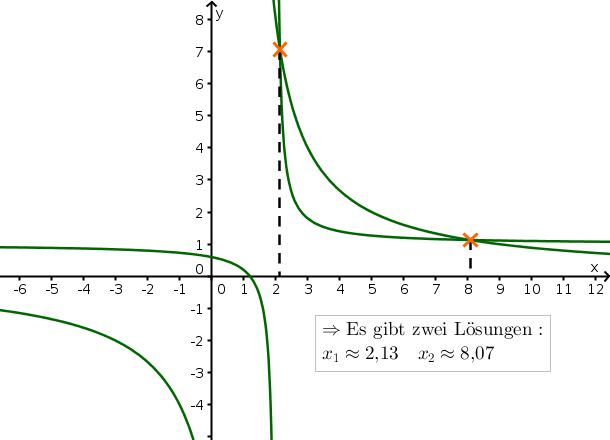
24 Beispiel zur leeren Lösungsmenge
25 Übungsaufgaben zu Bruchgleichung graphisch
Laden
Laden
26 Zusammenfassung
In diesem Kurs hast du sehr viel über Bruchgleichungen gelernt.
Definition
Eine Bruchgleichung hat drei wichtige Erkennungsmerkmale:
Es sind ein oder mehrere Brüche enthalten.
Eine Unbekannte tritt im Nenner auf.
Lösungsverfahren
Du hast einige wichtige Strategien zur Lösung einer Bruchgleichung gelernt. Bevor du die Gleichung löst, ist es wichtig, dass du zuerst die Definitionsmenge bestimmst.
Definitionsmenge
Die Definitionsmenge einer Bruchgleichung besteht aus allen Zahlen, die du für die Variable einsetzen darfst. Kein Nenner darf ergeben.
Methode: Über-Kreuz-Multiplizieren
Bestehen beide Seiten der Gleichung aus einem Bruch, kannst du folgendermaßen rechnen.
Hauptnenner-Methode

Graphische Lösung
Kennst du Graphen zu den Termen links und rechts des Gleichheitszeichens, kannst du die Lösung anhand der Schnittpunkte ablesen.
27 Weitere Übungsaufgaben
Hier findest du weitere Übungsaufgaben:
Und hier findest du eine Übersicht zu allen Lerninhalten zum Thema Bruchgleichungen.