Gruppe A
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Gib diejenige Zahl an, mit der man 1.000 multiplizieren muss, um -250 zu erhalten. (1 BE)
- 2
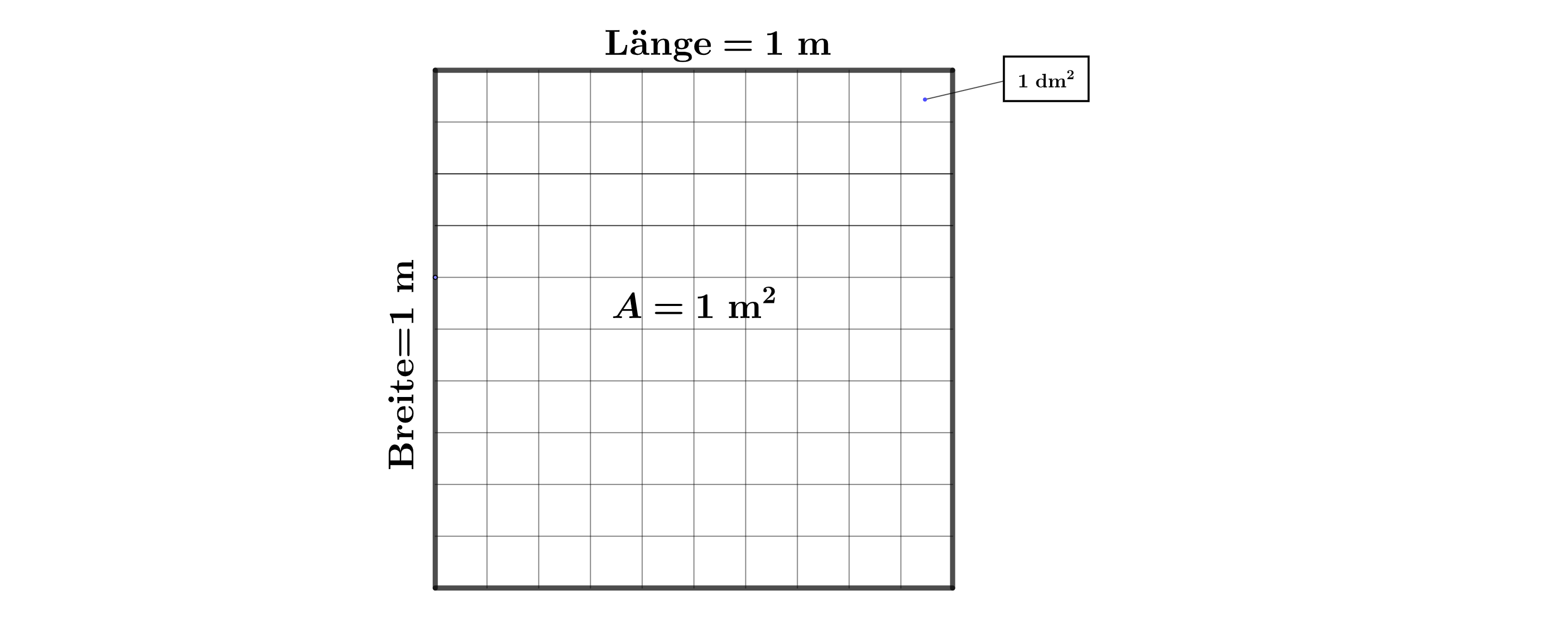
Begründe durch Anfertigen einer beschrifteten Skizze, dass gilt. (2 BE)
- 3
In einem Zeitungsartikel ist zu lesen: „Beim gestrigen Unwetter wurde eine Niederschlagshöhe von 15 mm erreicht." Ermittle, wie viele Liter Wasser bei diesem Unwetter auf einen Quadratmeter einer horizontalen Fläche fielen, indem du das Volumen eines Quaders mit einer Grundfläche von einem Quadratmeter und einer Höhe von 15 mm berechnest. (2 BE)
- 4
Bestimme die Lösung der Gleichung über der Grundmenge . (2 BE)
- 5
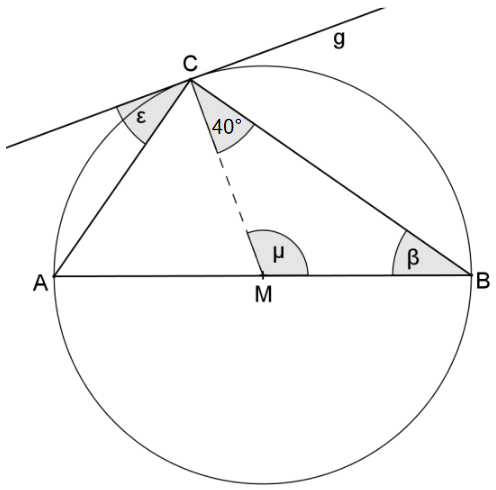
Die nicht maßstabsgetreue Abbildung zeigt das Dreieck , dessen Eckpunkte auf der Kreislinie um den Punkt liegen; die Strecke verläuft durch . Die Gerade ist eine Tangente an den Kreis und berührt diesen im Punkt .
a) Gib die Größe des Winkels und die Größe des Winkels an. Nenne zu jeder Antwort ein begründendes Stichwort. (2 BE)
b) Marie hat herausgefunden, dass gilt. Ergänze sinnvoll, was sie einer Mitschülerin dazu erklären könnte: (2 BE)
- 6
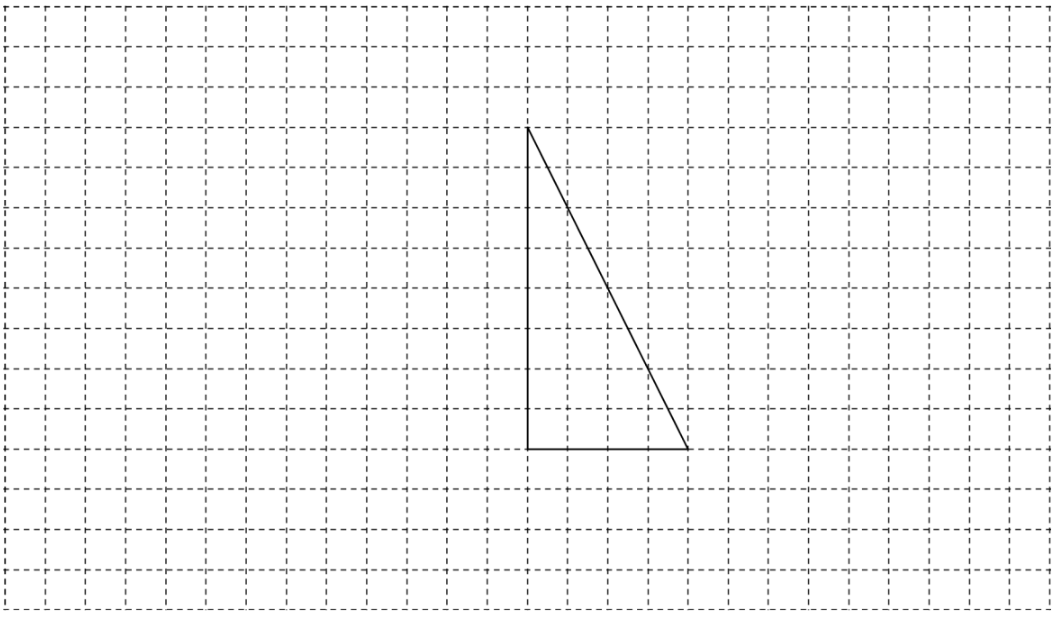
Ergänze das im Gitternetz abgebildete Dreieck so zu einer achsensymmetrischen Figur, dass der Inhalt des Dreiecks des Inhalts der Gesamtfläche der Figur beträgt. (2 BE)
- 7
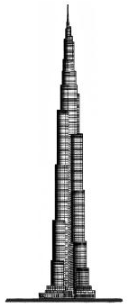
Der Burj Khalifa in Dubai ist mit Höhe derzeit das höchste Gebäude der Welt. Die Abbildung zeigt das Gebäude maßstabsgetreu.
Kreuze an, in welchem Maßstab das Gebäude abgebildet ist. (1 BE)
Die Aussichtsplattform in der 124. Etage liegt höher als das Erdgeschoss. Dorthin führt vom Erdgeschoss aus - ohne Zwischenhalt - ein Expressaufzug, der im Mittel pro Sekunde an Höhe gewinnt bzw. verliert. Der Expressaufzug fasst bis zu 25 Personen. Schätze die maximale Anzahl der Personen ab, die mit diesem Aufzug pro Stunde zur Aussichtsplattform transportiert werden können. Berücksichtige dabei auch die Zeit, die für das Ein- und Aussteigen nötig ist. (2 BE)
Hinweis: Bei einer Abschätzung muss grundsätzlich der Lösungsweg nachvollziehbar sein.
Für einige Wohnungen im Burj Khalifa ist der Preis pro Quadratmeter seit Eröffnung des Gebäudes um gefallen. Berechne, wie hoch der Preis pro Quadratmeter bei Eröffnung war, wenn er jetzt beträgt. (2 BE)
- 8
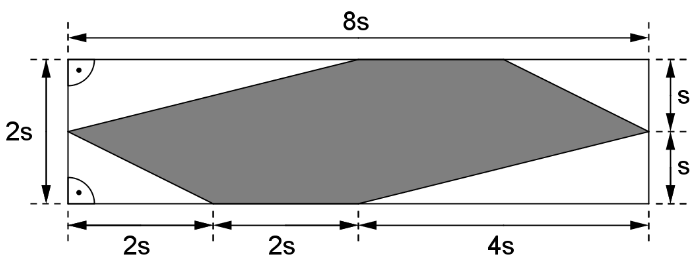
In der Abbildung ist eine punktsymmetrische Figur grau markiert.
Zeige durch Rechnung, dass der Flächeninhalt der grau markierten Figur beträgt. (2 BE)
Gib an, wie groß sein muss, damit der Flächeninhalt der grau markierten Figur beträgt; verwende den in Aufgabe 7 a angegebenen Term. (1 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?