Teil B, Gruppe 2
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Die Eisdiele Abruzzo verkaufte an einem Samstag insgesamt 540 Kugeln Eis. Sie bietet die Sorten Schokolade, Vanille, Zitrone und Erdbeere an.
Vom Vanilleeis wurden 40 Kugeln weniger verkauft als vom Zitroneneis. Von der Sorte Erdbeere wurden viermal so viele Kugeln verkauft wie von der Sorte Vanille. Vom Schokoladeneis wurden 80 Kugeln verkauft.
Wie viele Kugeln Eis wurden von jeder Sorte verkauft?Löse mit Hilfe einer Gleichung. (4 Punkte)
- 2
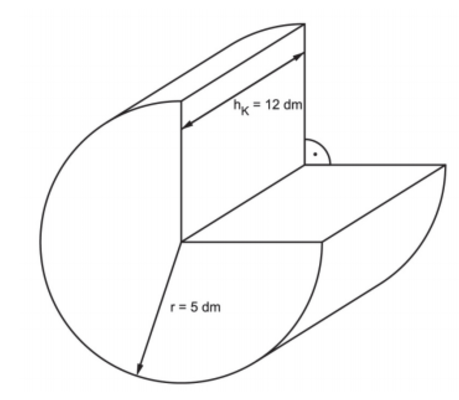
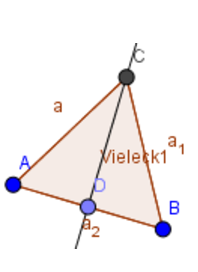
Aus einem Zylinder mit dem Radius und der Körperhöhe wird ein Viertel herausgeschnitten.Berechne die gesamte Oberfläche des entstandenen Körpers. (4 Punkte)
Hinweis: Skizze nicht maßstabgetreu
- 3
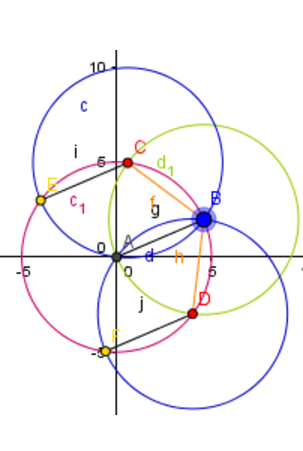
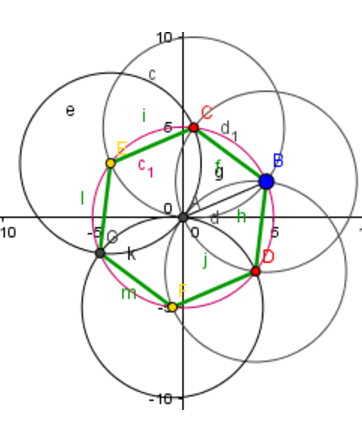
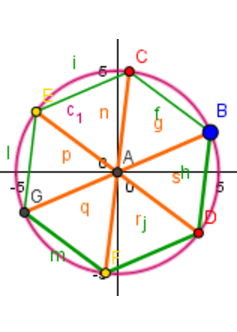
Löse die Aufgabe zum Sechseck. (4 Punkte)
Zeichne ein regelmäßiges Sechseck mit einer Seitenlänge von .
Berechne den Flächeninhalt des Secksecks. Runde auf zwei Nachkommastellen.
cm²
- 4
Charlotte interessiert sich für ein Mountainbike, einen Helm und ein paar Knieschoner. (4 Punkte)
Das Mountainbike kostet . Da es sich um ein Auslaufmodell handelt, erhält sie auf diesen Preis Rabatt. Berechne den neuen Fahrradpreis.
€Der Helm ist um reduziert und kostet jetzt noch . Ermittle rechnerisch, wie viele Euro sie beim Kauf des Helms spart.
€Der Preis der Knieschoner beträgt einschließlich Mehrwertsteuer . Hier bekommt sie die Mehrwertsteuer von ,,geschenkt''. Gib den Aktionspreis für die Knieschoner an.
€Charlotte kauft nur den Helm. Bei Barzahlung erhält sie auf ihren Einkauf nochmals Skonto. Berechne wie viel sie bezahlen muss.
€
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?