Aufgaben zum Aufstellen von Termen
- 1
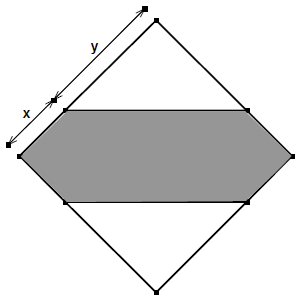
In das Quadrat ist ein grau gefärbter "Doppelpfeil" eingezeichnet.
Gib den Flächeninhalt des Doppelpfeils in Abhängigkeit von und an.
- 2
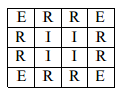
Beim Zerschneiden einer rechteckigen Pizza in waagrechte und senkrechte Streifen entstehen
Eckstücke (E),
reine Randstücke (R)
und Innenstücke (I),
siehe Abbildung für .
Stelle Terme auf, die die Zahl der Randstücke bzw. die Zahl der Innenstücke in Abhängigkeit von der Streifenzahl beschreiben.
- 3
Gegeben ist ein Quadrat mit der Seitenlänge . Bestimme den Term für den Flächeninhalt des Dreiecks .

- 4
Verlängert man jede Seite eines Dreiecks, so erhält man die Nebenwinkel der Innenwinkel , die sogenannten Außenwinkel . Was stellt der Term dar? Dieser Term lässt sich umformen zu . Was kann man daraus folgern?
- 5
Terme gliedern
Von welcher Art (Summe, Potenz oder …) ist der Gesamtterm:
Von welcher Art ist der Gesamtterm:
Gliedere den Term:
- 6
In einem Geschäft kostet ein Hammer Euro und Cent. Dazu kommen noch 19% MWSt.
Wie viel Cent kosten Hämmer einschließlich MWSt.? Welche Formel(n) ist /sind richtig?
- 7
In einem Hotel kostet die Übernachtung 70€. Hinzu kommen möglicherweise sonstige Kosten (Restaurant, Telefon, etc.) Auf all das werden noch 16% MWSt erhoben. Gesucht ist eine Formel für den Rechnungsbetrag (in €) als Funktion der Zahl der Nächte und den sonstigen Kosten (in €). Welche Formel ist richtig?
- 8
Stelle einen Term auf für den Mittelwert des Preises einer Ware in drei verschiedenen Geschäften:
Preis im ersten Geschäft: .
Preis im zweiten Geschäft: billiger als im ersten.
Preis im ersten Geschäft ist im höher als im dritten Geschäft.
- 9
Verbinde die Zahlen und mit Addition, Subtraktion oder Multiplikation (ohne Klammern zu setzen) und stelle so einen Term auf, dessen Wert …
positiv bzw. negativ ist,
so groß wie möglich ist,
so klein wie möglich ist,
möglichst nahe bei 0 liegt
- 10
Für ein Festessen sollen Einzeltische für je sechs Personen zu einer großen Tafel zusammengestellt werden. Es werden zwei Möglichkeiten betrachtet, dies zu tun: Die Tische können an den Schmal- oder Längsseiten zusammengestellt werden.

Wie viele Personen können bei jeder Tischanordnung insgesamt Platz nehmen, wenn eine bestimmte Anzahl Tische zusammengestellt werden?
Der Gastgeber hat so viele Gäste eingeladen, dass bei keiner der beiden möglichen Tischanordnungen Tische genügen. Wenn er einen weiteren Tisch hinzufügt, ist die Anzahl der Plätze genau ausreichend. Es wird davon ausgegangen, dass die Tische so aufgestellt werden, dass möglichst viele an einem Tisch Platz haben. Wie viele Personen nehmen am Festessen teil?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

