Exponentielles Wachstum (bzw. exponentieller Zerfall) beschreibt Änderungsprozesse, bei denen sich ein Wert in gleichen (zeitlichen) Abständen immer um denselben Faktor ändert.
Exponentielles Wachstum kann mit folgender Funktionsgleichung beschrieben werden:
Dabei ist:
die Anzahl bzw. Größe von einem Wert nach der Zeit bzw. nach Schritten,
die Anzahl bzw. Größe von einem Wert zur Zeit (oder vor dem ersten Schritt), also der Startwert,
den Wachstums- bzw. Zerfallsfaktor. Es gilt ist also eine positive, reelle Zahl und ungleich .
Diese Wachstumsfunktion gehört zu der Familie der Exponentialfunktionen. Sie besitzt daher alle Eigenschaften, die eine allgemeine Exponentialfunktion hat.
Einführung zum exponentiellen Wachstum
Plötzlich bricht die Zombieapokalypse aus! Es beginnt mit einem einzigen Zombie, der pro Stunde zwei weitere Menschen infiziert. Jeder neue Zombie tut es ihm gleich.
1. Frage: Wie viele Menschen sind nach 5 Stunden bereits zu Zombies geworden?
Nach einer Stunde hat der erste Zombie zwei Menschen infiziert.
Nach einer Stunde gibt es drei Zombies.
In der nächsten Stunde greift jeder der drei Zombies zwei weitere Menschen an. Insgesamt sind das weitere Menschen.
Nach zwei Stunden gibt es neun Zombies.
Nach drei Stunden wird es folglich weitere Zombies und insgesamt Zombies geben.
Man erkennt, dass die Anzahlen (3, 9, 27) Dreierpotenzen sind. Es liegt daher nahe, dass die Funktionsgleichung heißt, wobei die Anzahl der Zombies ist und in Stunden angegeben wird.
Das Ergebnis lautet also:
Innerhalb von 5 Stunden gibt es Zombies.
2. Frage: Wie lange dauert es, bis ganz Europa (742,5 Millionen Menschen) zu Zombies wurde?
Um dies beantworten zu können, muss man Exponentialgleichungen mithilfe des Logarithmus lösen können.
Gesucht ist der Zeitpunkt , bei dem gilt. Man setzt also den Funktionsterm gleich dem gegebenen und löst nach auf:
Mit den Logarithmusregeln folgt damit:
Auf eine ganze Zahl gerundet, lautet das Ergebnis:
Ganz Europa ist bereits nach 19 Stunden zombifiziert.
Halbwerts- und Verdopplungszeit
Die Begriffe Halbwerts- und Verdopplungszeit tauchen bei sehr vielen Vorgängen auf. Bei radioaktiven Materialien interessiert man sich ganz häufig für deren Halbwertszeiten, bei Geldanlagen will man dagegen die Verdopplungszeit wissen.
Wie ihre Namen schon verraten, geben sie den Zeitpunkt an, zu dem sich ein Startwert (wie die Startmenge eines Stoffes) halbiert bzw. verdoppelt hat.
Bestimmung des Wachstums- bzw. Zerfallsfaktors
Beim exponentiellen Wachstum
Der Wachstumsfaktor ergibt sich aus der Änderungsrate (). Im Einführungsbeispiel war , da immer zwei neue Zombies dazukamen.
(also ist )
Damit wird die Formel für das exponentielle Wachstum zu:
Beim exponentiellen Zerfall
Der Zerfallsfaktor ergibt sich aus der Änderungsrate . Man sagt Zerfallsfaktor und nicht Wachstumsfaktor, wenn .
(also ist )
Damit wird die Formel für den exponentiellen Zerfall zu:
Wachstumsgeschwindigkeit
Die Wachstumsgeschwindigkeit zu einer bestimmten Zeit ist definiert als die Ableitung zu dieser Zeit.
Die Ableitung der Wachstumsfunktion ist also:
Hier zeigt sich ein Vorteil der Beschreibung von Wachstumsprozessen mit der -Funktion. Denn damit lässt sich die Ableitung sehr leicht und schnell berechnen.
Mit der Zeit wird die Wachstumsgeschwindigkeit immer größer. Dies sieht man einmal am Graphen von monoton steigenden Exponentialfunktionen, der immer steiler wird. Man kann es sich auch mit Punktmengen veranschaulichen. Siehe dazu unten im Beispiel zum Bakterienwachstum.
Umgekehrt ist es bei Zerfallsprozessen. Die Zerfallsgeschwindigkeit ist zunächst sehr hoch und wird mit der Zeit schwächer.
Wichtige Beispiele
Bakterienwachstum
Ein Bakterium teilt sich nach jeder Stunde in zwei neue Bakterien. Jedes weitere Bakterium teilt sich auch wieder jede Stunde. Wie viele Bakterien sind es nach einem Tag?
Man schreibt zunächst die gegebenen Werte auf. Gesucht ist .
Dann setzt man in die Funktionsgleichung ein und berechnet den Wert.
Nach einem Tag sind es also Bakterien.
Graphische Veranschaulichung
Im nebenstehenden Bild wird die steigende Wachstumsgeschwindigkeit anhand der zu den Bakterien gehörenden Funktionsgleichung verdeutlicht.
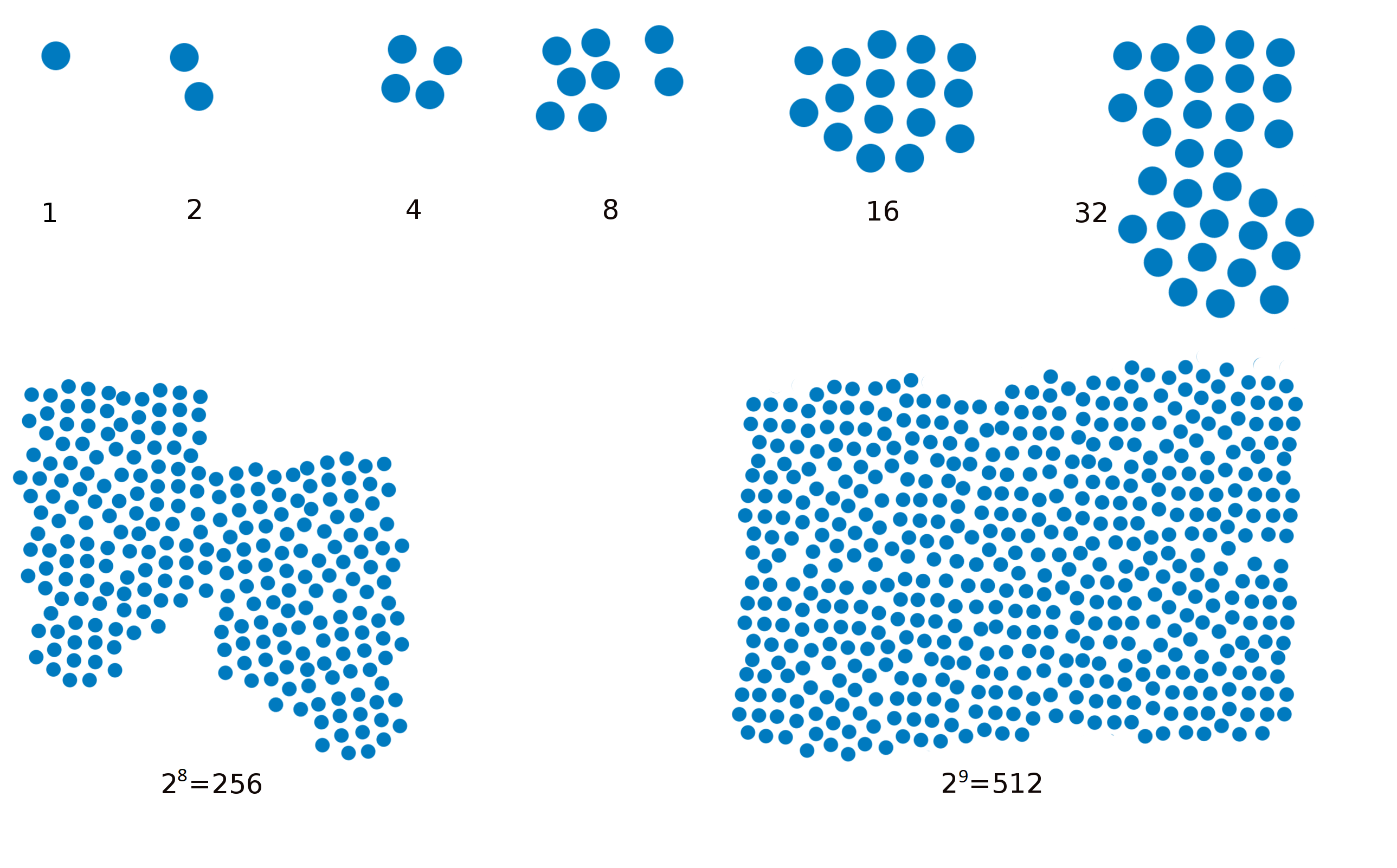
Zinseszinsrechnung
Man legt bei einer jährlichen Verzinsung von an. Wie viel Geld hat man nach Jahren?
Man schreibt zunächst die gegebenen Werte auf. Gesucht ist .
Dann setzt man in die Funktionsgleichung ein und berechnet den Wert.
Nach Jahren hat man also .
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Wachstums- und Zerfallsprozessen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
