Schnittpunkte von Funktionen sind genau die Punkte, an denen beide Funktionen den gleichen -Wert besitzen. In diesem Artikel wird erklärt, wie man diesen Punkt berechnet.
Mit diesem Wissen lassen sich die Schnittpunkte zweier Funktionen bestimmen.
Da die -Werte gleich sein sollen, setzt man die -Werte der beiden Funktionen gleich. Anschließend kann die entstehende Gleichung nach aufgelöst werden, wodurch man den -Wert des Schnittpunktes erhält.
Um den -Wert des Schnittpunktes zu erhalten, muss man nun noch den -Wert in eine der Funktionen einsetzen und den -Wert berechnen. Da die Funktionswerte gleich sind, ist es egal, in welche Funktion man einsetzt.
Grundsätzliches Vorgehen bei der Schnittpunktberechnung
Gesucht sind die Schnittpunkte der Funktionen und . Um diese zu berechnen, musst du die Funktionsterme gleichsetzen und diese Gleichung anschließend nach auflösen.
Damit erhältst du die -Koordinate . Nun berechnest du die -Koordinate, indem du diesen -Wert in eine der Funktionen einsetzt:
Der Schnittpunkt der beiden Funktionen und liegt also bei . Dies ist der einzige Schnittpunkt.
Berechnung der Schnittpunkte bei bestimmten Funktionen
Zwei Geraden
Der Schnittpunkt zweier Geraden ist eindeutig. Er lässt sich durch Gleichsetzen der Funktionsterme bestimmen.
Beispiel
Bestimme den Schnittpunkt von
und .
Dafür setzt du zunächst die -Werte gleich und löst anschließend nach auf:
Um die -Koordinate des Schnittpunkts der beiden Funktionen zu bestimmen, setzt du den eben berechneten -Wert in eine der beiden Funktionsgleichungen ein und berechnest den Wert:
Polynom und Gerade
Schneidet man ein Polynom mit einer Gerade, dann ist die Anzahl der Schnittpunkte höchstens gleich dem Grad des Polynoms.
Bei der Berechnung setzt man wieder zu Beginn die Funktionswerte gleich. Anschließend bringt man alles auf eine Seite und bestimmt die Nullstellen der neuen Funktion, falls nötig, mit der Mitternachtsformel oder durch Polynomdivision.
Beispiel
Bestimme die Schnittpunkte von und . Dazu setzt du zunächst die -Werte gleich und bringst alles auf eine Seite:
Nun suchst du die Nullstellen der neuen Funktion .
In diesem Fall findest du die erste Nullstelle durch Ausklammern von x:
Es gilt also:
Die übrigen Nullstellen, also die Nullstellen des Restterms , lassen sich mit der Mitternachtsformel bestimmen:
Einsetzen dieser drei -Werte in eine der Funktionen liefert die zugehörigen -Werte und damit die Schnittpunkte A, B und C:
Video zur Berechnung von Schnittpunkten
Laden
Zwei Polynome
Hat man zwei Polynome, dann ist das Vorgehen analog zum Vorgehen bei einem Polynom und einer Gerade:
Zuerst setzt du die Funktionsterme gleich. Anschließend bringst du alles auf eine Seite und berechnest die Nullstellen dieser neuen Funktion.
Beispiel
Bestimme die Schnittpunkte von und .
Setzt du die beiden Funktionsterme gleich, siehst du sofort, dass der quadratische Term wegfällt:
Einsetzen dieser -Werte in eine der Funktionsgleichungen liefert die zugehörigen -Werte und damit die Schnittpunkte A und B:
Beliebige Funktionen
Bei beliebigen Funktionen kann es beliebig schwierig werden, die Schnittpunkte zu bestimmen. Man kann zwar weiterhin die -Werte gleichsetzen, aber das auflösen nach oder die Nullstellenbestimmung bei der neuen Funktion sind ohne Hilfsmittel fast nicht zu lösen.
Ein mögliches Hilfsmittel zur Nullstellenbestimmung ist das Newtonsche Näherungsverfahren.
Beispiel
Bestimme den Schnittpunkt von und . Dazu setzt du zunächst wieder beide Funktionen gleich:
Die Nullstelle der neuen Funktion sind nicht so leicht zu erkennen oder zu berechnen. Deshalb verwendest du das Näherungsverfahren. Dafür benötigst du die erste Ableitung der neuen Funktion sowie einen Startpunkt in der Nähe der Nullstelle von .
Da stetig ist, folgt wegen
und ,
dass die Nullstelle von zwischen und liegen muss. Wähle zum Beispiel und bestimme . Damit führst du nun den ersten Schritt des Näherungsverfahrens durch:
Nach wenigen Iterationen liefert das Verfahren das Ergebnis .
Um den zu gehörigen -Wert zu berechnen, setzt du in eine der Funktionsgleichungen ein:
Der Schnittpunkt liegt also ungefähr bei
Schnittpunkte bei Funktionenscharen
Enthält ein Funktionsterm einen Parameter, so spricht man von einer Funktionenschar.
Eine genaue Betrachtung von Schnittpunkten bei Funktionenscharen findet sich im Artikel Funktionenbündel / Gemeinsamer Punkt von Funktionenscharen.
Im Folgenden findest du verschiedene Beispiele für Funktionenscharen und deren Schnittpunkte.
Eindeutiger Schnittpunkt
Eine Funktionenschar kann einen gemeinsamen Schnittpunkt haben. Will man diesen bestimmen, so wählt man für den Parameter zwei verschiedene Werte und bestimmt den Schnittpunkt dieser beiden Funktionen.
Beispiel
Bestimme den Schnittpunkt der Funktionenschar . Dafür wählst du zwei beliebige, verschiedene Werte für den Parameter , also beispielsweise und . Nun setzt du die beiden Funktionsterme gleich und löst nach auf:
Dies ist die -Koordinate des Schnittpunkts der Funktionenschar. Um die -Koordinate des Schnittpunkts zu berechnen, setzt du den -Wert in eine der beiden Funktionsgleichungen ein:
Damit ergibt sich der Schnittpunkt .
Wechselnde Schnittpunkte
Kommt ein Parameter mehrmals und/oder potenziert vor, so muss es keinen eindeutigen Schnittpunkt geben.
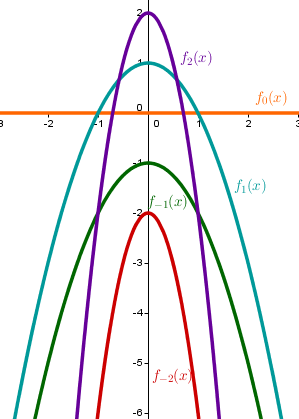
Das nebenstehende Bild zeigt die Funktionsgraphen der Funktionenschar
für
Offensichtlich gibt es keinen eindeutigen Schnittpunkt.
Übungsaufgaben
Laden
Laden
Laden
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Berechnung von Schnittpunkten von Geraden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
