Eine reelle Funktion (d.h. eine Funktion, deren Definitionsmenge eine Teilmenge von ist und nur Werte in hat) heißt monoton steigend (oder monoton wachsend), wenn für alle aus der Definitionsmenge gilt:
Eine reelle Funktion monoton fallend, wenn für alle aus der Definitionsmenge gilt:
Anschaulich bedeutet das: Wird der -Wert größer, so wird bei einer monoton steigenden Funktion auch der Funktionswert größer oder bleibt gleich. Genauso nennt man eine Funktion monoton fallend, wenn die Funktionswerte bei wachsendem kleiner werden oder gleich bleiben.
Die Betrachtung des Monotonieverhaltens einer Funktion ist fester Bestandteil der Kurvendiskussion. Im Artikel Monotonieverhalten berechnen wird erklärt, wie sich das Monotonieverhalten einer Funktion untersuchen lässt.
Strenge Monotonie
Strenge Monotonie ist eine stärkere Eigenschaft als einfache Monotonie.
Eine Funktion heißt streng monoton steigend, wenn gilt:
Sie ist streng monoton fallend, wenn gilt
Der Unterschied zu der einfachen Monotonie besteht darin, dass keine konstanten Abschnitte mehr erlaubt werden. Beachte, dass die Ungleichungen jetzt anders formuliert sind.
Beispiele
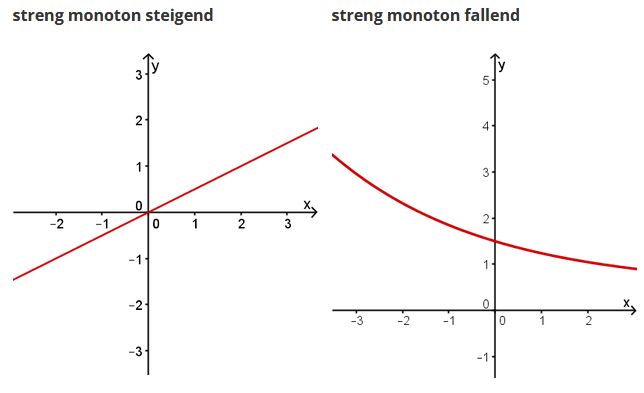
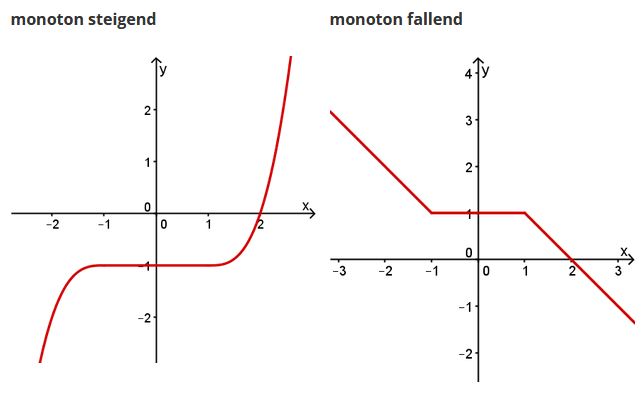
Bezug zur Ableitung
Ist die Funktion differenzierbar, so lässt sich die Monotonie an der Ableitung ablesen:
Kriterium | Monotonie |
|---|---|
für alle | ist monoton steigend |
für alle | ist streng monoton steigend |
für alle | ist monoton fallend |
für alle | ist streng monoton steigend |
Dies wird beim Vorzeichenkriterium zur Charakterisierung von Extrema ausgenutzt.
Monotonieintervalle
Viele Funktionen sind nicht auf ihrem gesamten Definitionsbereich monoton steigend oder fallend, sondern nur auf bestimmten Intervallen. So ist z. B. streng monoton fallend im Intervall und streng monoton steigend im Intervall .
Diese Intervalle heißen Monotonieintervalle von . Diese Intervalle werden durch Klammern angegeben, wobei darauf zu achten ist, dass der Rand des Intervalls nicht darin enthalten ist. Grund dafür ist, dass zwischen diesen Intervallen keine strenge Monotonie herrscht.
Beispiel Monotonieintervalle
Die Funktion ist im roten Bereich monoton steigend und im blauen Bereich monoton fallend.
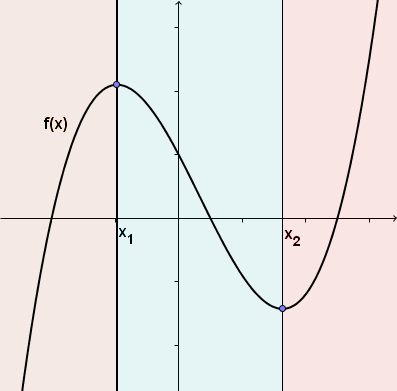
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Monotonieverhalten
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
