Übungsaufgaben zu trigonometrischen Funktionen

Hier findest du gemischte Aufgaben zu trigonometrischen Funktionen und Termen. Lerne, Funktionsterme aufzustellen und Terme zu vereinfachen!

1
Vereinfache und fasse soweit wie möglich zusammen:
1. $\frac{1 - (\cos (α))^{2}}{\sin (α) \cdot \sin (90 ° - α)} - \tan (α)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrische Funktionen
  Gegeben:
  $\frac{1 - (\cos (a))^{2}}{\sin (a) \cdot \sin (90 ° - a)} - \tan (a)$
  Verwende den trigonometrischen Pythagoras:
  $\sin^{2} (a) + \cos^{2} (a) = 1$
  Damit kannst du den Zähler vereinfachen.
  $= \frac{\sin^{2} (a)}{\sin (a) \cdot \sin (90 ° - a)} - \tan (a)$
  Kürze im Bruch mit $\sin (a)$ .
  $= \frac{\sin (a)}{\sin (90 ° - a)} - \tan (a)$
  Wegen der Komplementbeziehung gilt:
  $\sin (90 ° - a) = \cos (a)$ .
  $= \frac{\sin (a)}{\cos (a)} - \tan (a)$
  Benutze die Definition der Tangensfunktion.
  $= \tan (a) - \tan (a) = 0$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $\frac{{(\cos (x + \frac{π}{2}))}^{2}}{1 - {(\frac{\sin (x)}{\tan (x)})}^{2}} + \frac{\sin (x) - \tan (x)}{\tan (x)}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrische Funktionen
  Gegeben:
  $\frac{{(\cos (x + \frac{π}{2}))}^{2}}{1 - {(\frac{\sin (x)}{\tan (x)})}^{2}} + \frac{\sin (x) - \tan (x)}{\tan (x)}$
  Ziehe den hinteren Bruch auseinander.
  $= \frac{{(\cos (x + \frac{π}{2}))}^{2}}{1 - {(\frac{\sin (x)}{\tan (x)})}^{2}} + \frac{\sin (x)}{\tan (x)} - \frac{\tan (x)}{\tan (x)}$
  $= \frac{{(\cos (x + \frac{π}{2}))}^{2}}{1 - {(\frac{\sin (x)}{\tan (x)})}^{2}} + \frac{\sin (x)}{\tan (x)} - 1$
  Aus der Formel für den Tangens folgt:
  $\tan (x) = \frac{\sin (x)}{\cos (x)} | \cdot \cos (x)$
  $\tan (x) \cdot \cos (x) = \sin (x) | : \tan (x)$
  $\cos (x) = \frac{\sin (x)}{\tan (x)}$
  Ersetze also $\frac{\sin (x)}{\tan (x)}$ durch $\cos (x)$
  $= \frac{{(\cos (x + \frac{π}{2}))}^{2}}{1 - {(\frac{\sin (x)}{\tan (x)})}^{2}} + \cos (x) - 1$
  Ersetze $\frac{\sin (x)}{\tan (x)}$ im Nenner des Bruches durch $\cos (x)$
  $= \frac{{(\cos (x + \frac{π}{2}))}^{2}}{1 - (\cos (x))^{2}} + \cos (x) - 1$
  Wenn du die Kosinusfunktion um $\frac{π}{2}$ verschiebt, also $\cos (x + \frac{π}{2})$ , erhältst du $- \sin (x)$ .
  $= \frac{(- \sin (x))^{2}}{1 - (\cos (x))^{2}} + \cos (x) - 1$
  Es gilt allgemein $(- x)^{2} = x^{2}$ , also auch $(- \sin (x))^{2} = (\sin (x))^{2}$ .
  $= \frac{(\sin (x))^{2}}{1 - (\cos (x))^{2}} + \cos (x) - 1$
  Verwende den trigometrischen Pythagoras:
  $(\sin (x))^{2} + (\cos (x))^{2} = 1 | - (\cos (x))^{2}$
  $(\sin (x))^{2} = 1 - (\cos (x))^{2}$
  $= \frac{(\sin (x))^{2}}{(\sin (x))^{2}} + \cos (x) - 1$
  $= 1 + \cos (x) - 1$
  $= \cos (x)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Bestimme die Funktionsgleichung zu folgenden Graphen:

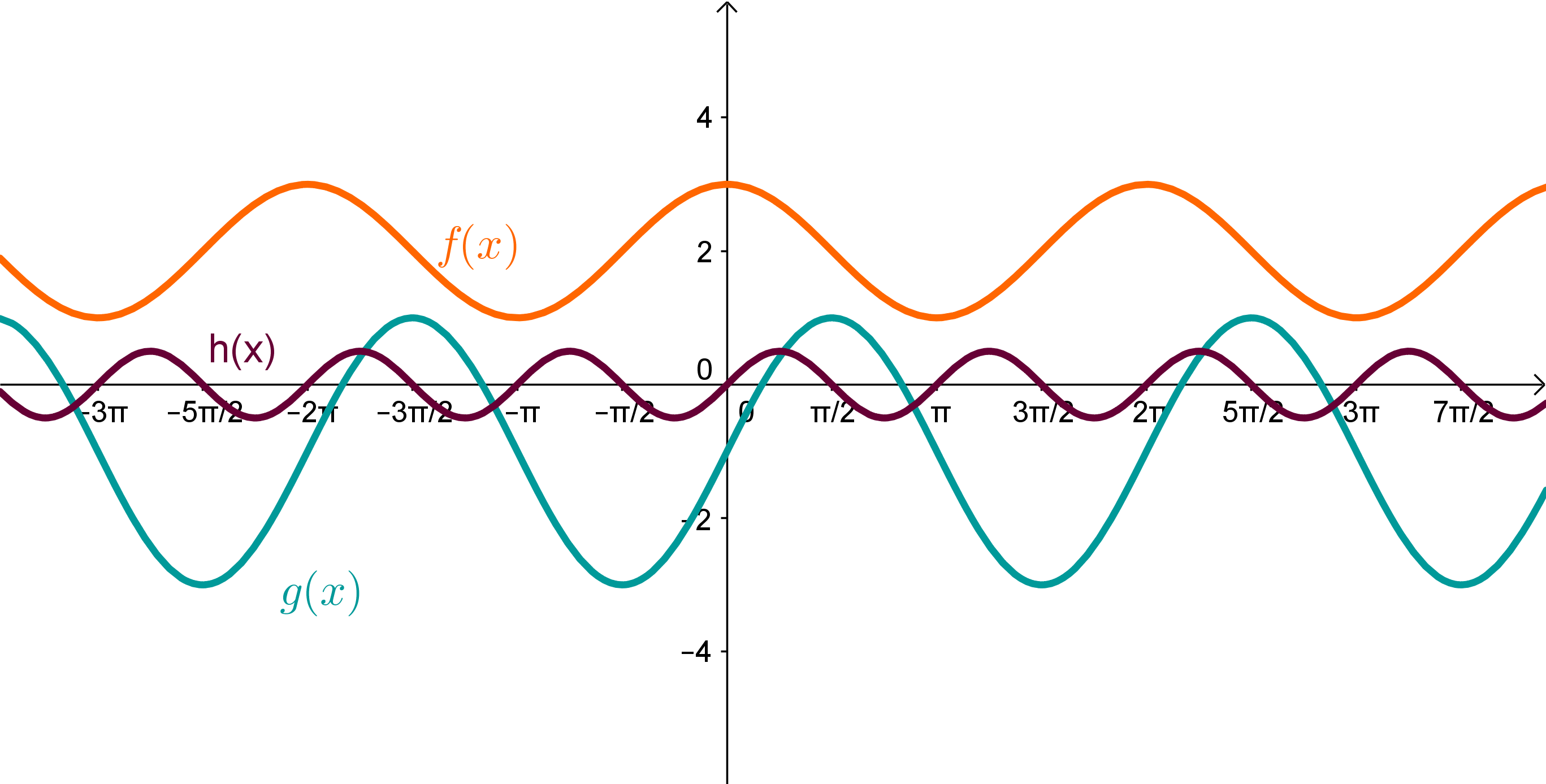
Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrische Funktionen
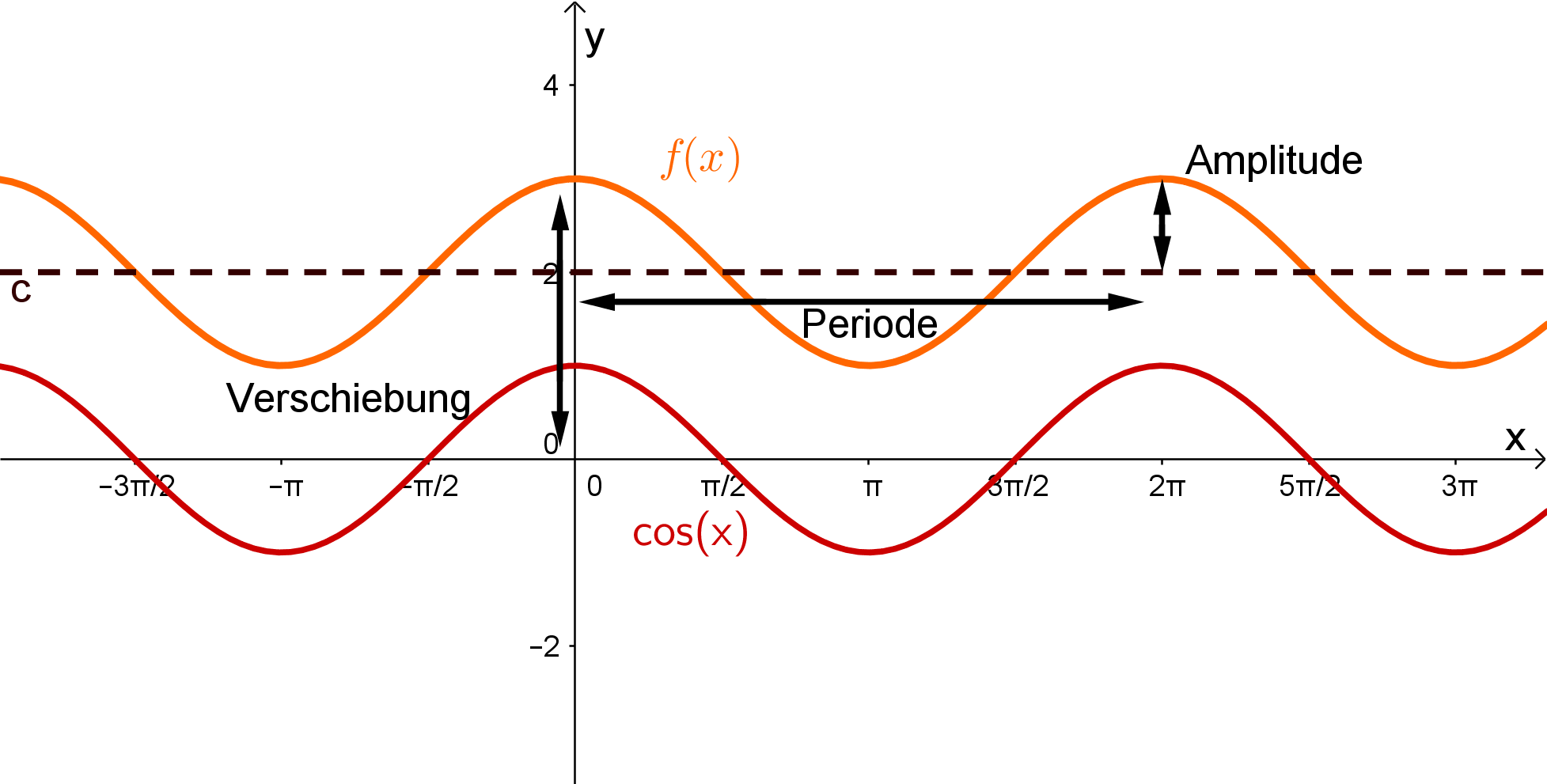
Lösung für die Funktion $f (x)$ :
Aufgrund der Achsensymmertrie muss es sich um eine Kosinus-Funktion handeln.
Du kannst die Kosinus-Funktion $\cos (x)$ verschieben und strecken, mit der allgemeinen Funktionsgleichung: $a \cdot \cos (b \cdot (x + c)) + d$ .
Betrachtest du die Amplitude der Funktion, siehst du das diese $1$ beträgt, also genau so groß wie bei der normalen Kosinus-Funktion $\cos (x)$ , dass heißt für die allgemeine Funktionsgleichung, das $a$ den Wert $1$ haben muss, weil man die Amlitupde der $\cos (x)$ Funktion nicht verändert.
Ebenfalls siehst du, dass der Graph der gesuchten Funktion die selbe Periode wie die $\cos (x)$ Funktion, das bedeutet, $b$ aus der allgemeinen Form muss den Wert $1$ haben.
Nachdem die gesuchte Funktion auch nicht nach rechts oder links verschoben wurde,muss der Wert von $c$ aus der allgemeinen Form $0$ sein.
Jetzt musst du also nur noch die Verschiebung des Graphen der gesuchten Funktionnach oben betrachten. Der Graph der gesuchten Funktion wurde um $2$ nach oben verschoben, das heißt, $d$ aus der alllgemeinen Form hat den Wert $2$ .
Fasst du nun alle Werte der Variablen zusammen, $a = 1, b = 1, c = 0, d = 2$ , erhälst du folgende Lösung für die gesuchte Funktion $f (x)$ :
$f (x) = 1 \cdot \cos (1 \cdot (x + 0)) + 2 = \cos (x) + 2$
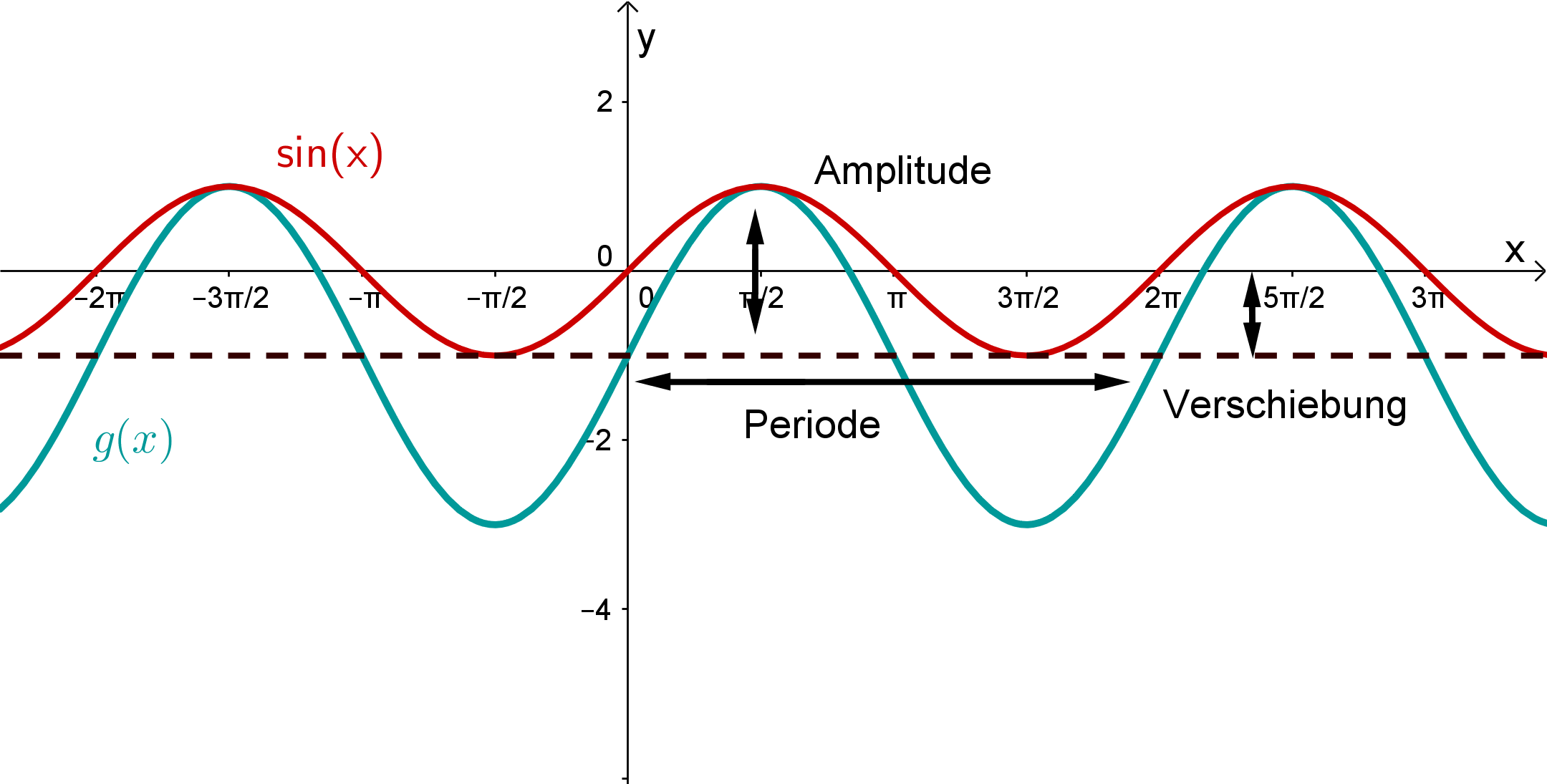
Lösung für die Funktion g(x):
Aufgrund der Punktsymmetrie bezüglich des Punktes (-1|0) muss es sich um eine Sinus-Funktion handeln.
Du kannst die Sinus-Funktion $\sin (x)$ verschieben und strecken, mit der allgemeinen Funktionsgleichung: $a \cdot \sin (b \cdot (x + c)) + d$ .
Betrachtest du die Amplitude der Funktion, siehst du, dass diese $2$ beträgt, das heißt für die allgemeine Funktionsgleichung, dass $a$ den Wert $2$ haben muss, weil die Amplitude der gesuchten Funktion doppelt so groß ist wie die der $\sin (x)$ Funktion.
Du siehst, dass der Graph der gesuchten Funktion die selbe Periode hat wie die $\sin (x)$ Funktion, das bedeutet, $b$ aus der allgemeinen Form muss den Wert $1$ haben.
Die gesuchte Funktion wurde auch nicht nach rechts oder links verschoben ,deshalb muss der Wert von $c$ aus der allgemeinen Form $0$ sein.
Betrachtest du die Verschiebung des Graphen nach unten, stellst du fest, dass die gesuchte Funktion um $1$ nach unten verschoben wurde, also hat $d$ aus der allgemeinen Form den Wert $- 1$ ,
Fasst du nun alle Werte der Variablen zusammen, $a = 2, b = 1, c = 0, d = - 1$ , erhälst du folgende Lösung für die gesuchte Funktion $g (x)$ :
$g (x) = 2 \cdot \sin (1 \cdot (x + 0)) - 1 = 2 \cdot \sin (x) - 1$
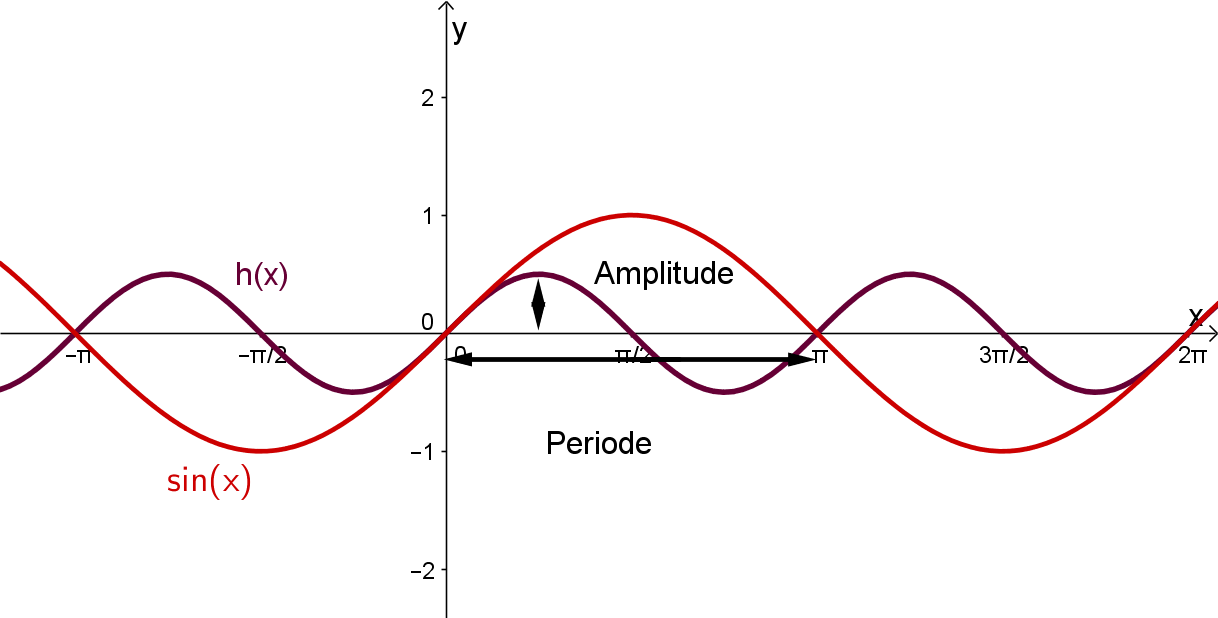
Lösung für die Funktion h(x):
Aufgrund der Punktsymmetrie bezüglich des Ursprungs muss es sich um eine Sinus-Funktion handeln.
Du kannst die Sinus-Funktion $\sin (x)$ verschieben und strecken, mit der allgemeinen Funktionsgleichung: $a \cdot \sin (b \cdot (x + c)) + d$ .
Betrachtest du die Amplitude der Funktion, siehst du, dass diese $\frac{1}{2}$ beträgt, das heißt für die allgemeine Funktionsgleichung, dass $a$ den Wert $\frac{1}{2}$ haben muss, weildie Amlitude der gesuchten Funktion halb so groß ist wie die der $\sin (x)$ Funktion.
Betrachtest du die Periode des Graphen der gesuchten Funktion, siehst du, dass diese im Vergleich zur $\sin (x)$ nur halb so groß ist(oder auch: der Sinus "läuft" doppelt so schnell). Das heißt, dass $b$ in unserer allgemeinen Form hat den Wert $2$ .
Der Graph der Funktion wurde im Vergleich zu $\sin (x)$ auch nicht nach rechts oder links verschoben, das heißt der Wert von $c$ in der allgemeinen Form beträgt $0$ .
Vergleichst du den Graph mit der $\sin (x)$ Funktion, siehst du, dass dieser nicht nach oben oder unten verschoben wurde, deshalb hat $d$ aus der allgemeinen Form den Wert $0$ .
Fasst du nun alle Werte der Variablen zusammen, $a = \frac{1}{2}, b = 2, c = 0, d = 0$ , erhält man folgende Lösung für die gesuchte Funktion $h (x)$ :
$h (x) = \frac{1}{2} \cdot \sin (2 \cdot (x + 0)) + 0 = \frac{1}{2} \cdot \sin (2 \cdot x)$
3
Berechne alle Winkel $α$ zwischen $0 °$ und $360 °$ , die folgende Gleichung erfüllen:
$[4 \cdot \sin (2 \cdot α) - (\sqrt{6} + \sqrt{2})] \cdot [{(\tan (\frac{α}{3}))}^{2} + 2 \cdot \sqrt{5} - 5] = 0$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrische Umkehrfunktion
$[4 \cdot \sin (2 \cdot α) - (\sqrt{6} + \sqrt{2})] \cdot [{(\tan (\frac{α}{3}))}^{2} + 2 \cdot \sqrt{5} - 5] = 0$
Die Gleichung ist $0$ , wenn einer der beiden Faktoren $0$ ist.
$[4 \cdot \sin (2 \cdot α) - (\sqrt{6} + \sqrt{2})] = 0$ oder $[{(\tan (\frac{α}{3}))}^{2} + 2 \cdot \sqrt{5} - 5] = 0$
Betrachte zunächst den ersten Faktor:
$\begin{array}{rcll} 4 \cdot \sin (2 \cdot α) - (\sqrt{6} + \sqrt{2}) & = & 0 & | + (\sqrt{6} + \sqrt{2}) \\ 4 \cdot \sin (2 \cdot α) & = & \sqrt{6} + \sqrt{2} & | \div 4 \\ \sin (2 \cdot α) & = & \frac{\sqrt{6} + \sqrt{2}}{4} & | \sin^{- 1} (\dots) \\ 2 \cdot α & = & \sin^{- 1} (\frac{\sqrt{6} + \sqrt{2}}{4}) & | \div 2 \\ α & = & \frac{\sin^{- 1} (\frac{\sqrt{6} + \sqrt{2}}{4})}{2} \end{array}$
Die rechte Seite der Gleichung kannst du nun mit dem Taschenrechner berechnen.
$α = 37,5 °$
Überprüfe nun, ob außer $α = 37,5 °$ noch weitere Winkel eine Lösung sein können. Betrachte dazu zum Beispiel den Einheitskreis:
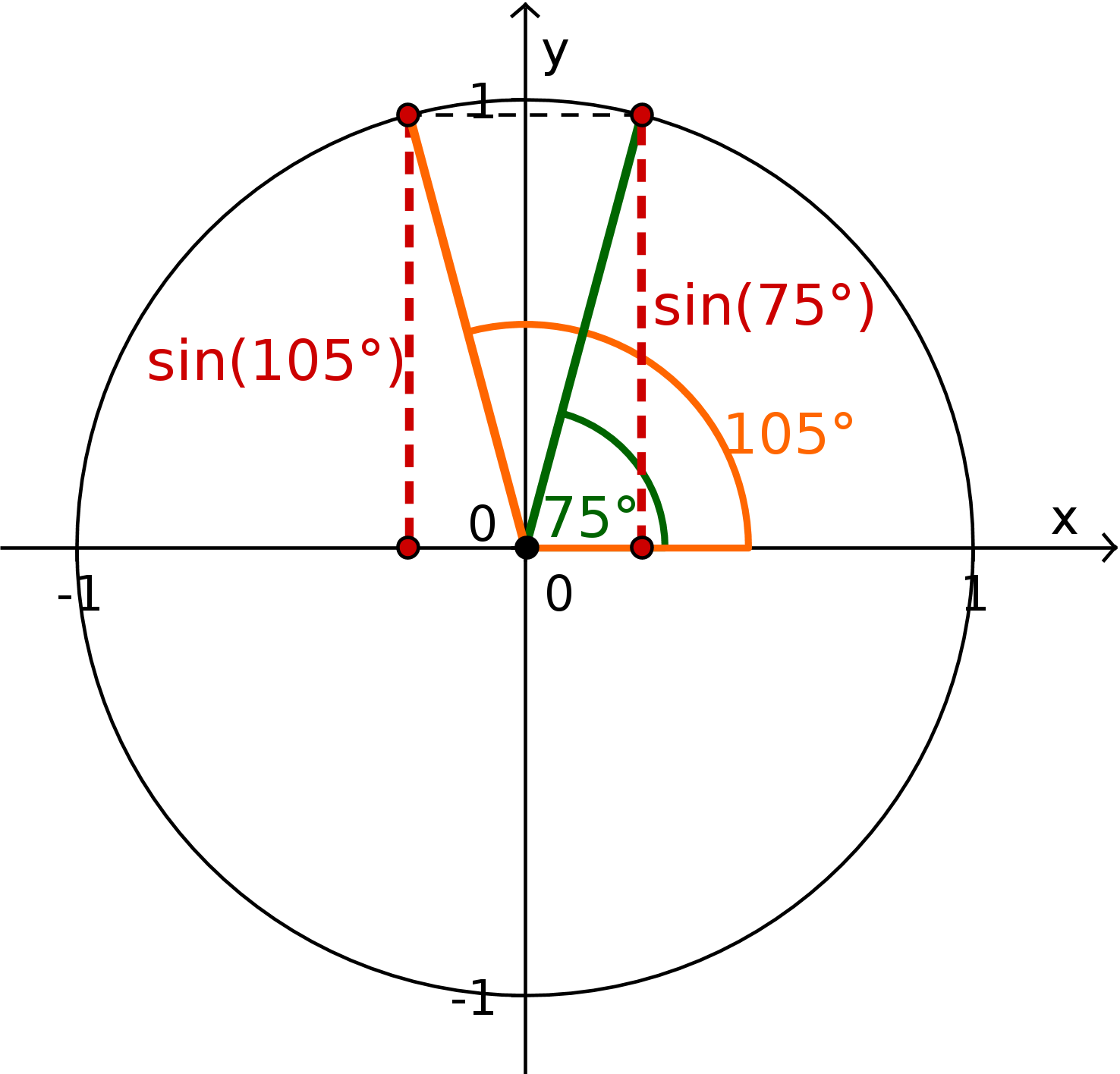
Hier kannst du sehen, dass der Sinus für zwei Winkel den gleichen Wert annimmt. $\sin (75 °) = \sin (180 ° - 75 °) = \sin (105 °)$ . Daraus folgt $2 α = 105 °$ . Das heißt, $α = 52,5 °$ ist eine weitere Lösung.
Betrachte als nächstes den zweiten Faktor.
$\begin{array}{rclll} {(\tan (\frac{α}{3}))}^{2} + 2 \cdot \sqrt{5} - 5 & = & 0 | - 2 \cdot \sqrt{5} | + 5 \\ {(\tan (\frac{α}{3}))}^{2} & = & - 2 \cdot \sqrt{5} + 5 & | \sqrt{} \\ \tan (\frac{α}{3}) & = & \pm \sqrt{- 2 \cdot \sqrt{5} + 5} & | \tan^{- 1} (\dots) \\ \frac{α}{3} & = & \tan^{- 1} (\pm \sqrt{- 2 \cdot \sqrt{5} + 5}) & | \cdot 3 \\ α & = & 3 \cdot \tan^{- 1} (\pm \sqrt{- 2 \cdot \sqrt{5} + 5}) \end{array}$
Die rechte Seite der Gleichung kannst du nun mit dem Taschenrechner berechnen.
$α = \pm 108 °$

Gesucht sind Winkel zwischen $0 °$ und $360 °$ . Also ist $- 108 °$ keine gültige Lösung.
$α = 108 °$
Beachte: Für den Tangens gilt die Supplementbeziehung
$\tan (\frac{α}{3}) = \tan (\frac{α}{3} + 180 °) .$
Überprüfe damit, ob weitere Winkel eine Lösung sein können. Es folgt daraus, dass auch
$\tan (\frac{108 °}{3} + 180 °) = \tan (216 °) .$
Aber $\frac{α}{3} = 216 °$ ergibt $α = 648 °$ . Der Winkel ist größer als $360 °$ und damit keine Lösung. $108 °$ ist also von diesem Teil der Gleichung die einzige Lösung.
Insgesamt wird die Gleichung von allen $α \in {37,5 °; 52,5 °; 108 °}$ gelöst.

Das Wissenschaftsmagazin "I $♡$ physics " berichtet über eine herausragende Entdeckung. Zur Berechnung der Lichtwellenlänge $x$ soll folgende Formel gelten:

(\sin (x) + \frac{\sin (x)}{\tan (x)}) \cdot (\cos (x + \frac{π}{2}) - \cos (x)) - \frac{\cos (x - \frac{3}{2} \cdot π)}{\sin (x)} = 0

Ist diese Formel mathematisch allgemein gültig? Begründe deine Antwort rechnerisch!

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\tan (x)$	$=$	$\frac{\sin (x)}{\cos (x)}$	$\cdot \cos (x)$
$\tan (x) \cdot \cos (x)$	$=$	$\sin (x)$	$: \tan (x)$
$\cos (x)$	$=$	$\frac{\sin (x)}{\tan (x)}$

$(\sin (x) + \cos (x)) \cdot (\sin (x) - \cos (x)) + \frac{- \sin (x)}{\sin (x)}$	$=$	$0$
$(\sin (x) + \cos (x)) \cdot (\sin (x) - \cos (x)) + (- 1)$	$=$	$0$
$(\sin (x) + \cos (x)) \cdot (\sin (x) - \cos (x)) - 1$	$=$	$0$
	↓	Verwende die dritte binomische Formel
$(\sin (x))^{2} - (\cos (x))^{2} - 1$	$=$	$0$	$+ 1$
$(\sin (x))^{2} - (\cos (x))^{2}$	$=$	$1$

Übungsaufgaben zu trigonometrischen Funktionen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?