Damit ein Schnittwinkel existiert, müssen sich die geometrischen Objekte schneiden.
Weiterführende Artikel zur Lagenbestimmung von geometrischen Objekten
Schnittwinkel zwischen zwei Geraden
Zwei Geraden besitzen nur einen Schnittwinkel, wenn sie sich schneiden.
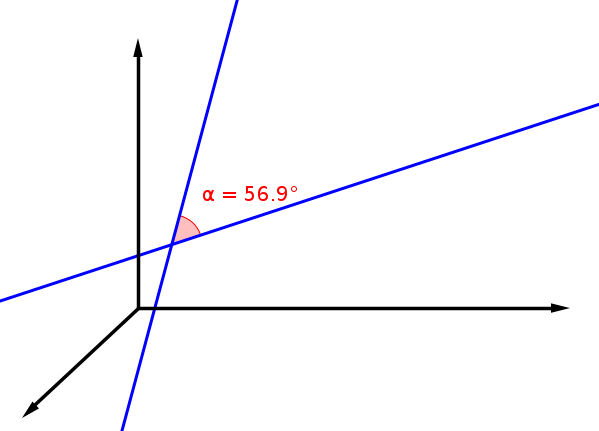
Seien die Richtungsvektoren der Geraden.
Dann lässt sich der Schnittwinkel so berechnen:
Beispiel
Gegeben sind zwei sich schneidende Geraden g und h:
und :
Berechne den Schnittwinkel .
Für die Winkelberechnung der beiden Geraden benötigst du ihre Richtungsvektoren und deren Beträge.
,
,
| ↓ | Setze die Vektoren und ihre Beträge ein. | ||
| ↓ | Berechne das Skalarprodukt und vereinfache. | ||
| ↓ | Vereinfache. | ||
| ↓ | Berechne den Betrag | ||
Du hast die Gleichung erhalten. Durch Anwendung der Umkehrfunktion des Kosinus kannst du den Winkel berechnen. Benutze auf dem Taschenrechner die Funktion .
Antwort: Der Schnittwinkel zwischen den beiden Geraden beträgt rund .
Schnittwinkel zwischen Ebene und Gerade
Eine Ebene und eine Gerade haben einen Schnittpunkt, solange sie nicht echt parallel sind.
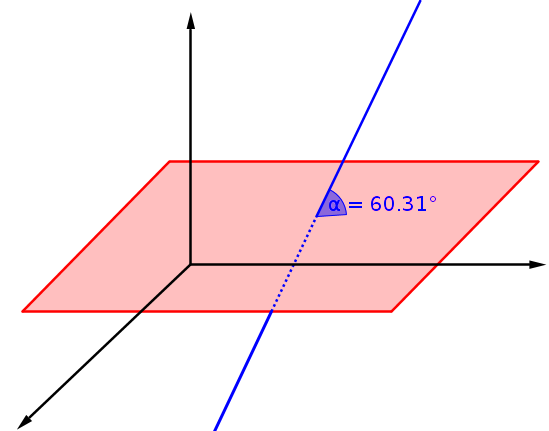
Sei der Normalenvektor der Ebene und der Richtungsvektor der Gerade.
Dann kann der Schnittwinkel so berechnet werden:
Eine weitere Möglichkeit ist, auszurechnen.
Beispiel
Gegeben sind eine Geraden g und eine Ebene :
und
Berechne den Schnittwinkel .
Für die Winkelberechnung zwischen Gerade und Ebene benötigst du von der Geraden den Richtungsvektor und dessen Betrag und von der Ebene den Normalenvektor und dessen Betrag.
,
,
Setze in die oben genannte Formel ein:
| ↓ | Setze die Vektoren und ihre Beträge ein. | ||
| ↓ | Berechne das Skalarprodukt und vereinfache. | ||
| ↓ | Vereinfache. | ||
| ↓ | Berechne den Betrag. | ||
Du hast die Gleichung erhalten. Durch Anwendung der Umkehrfunktion des Sinus kannst du den Winkel berechnen. Benutze auf dem Taschenrechner die Funktion .
Antwort: Der Schnittwinkel zwischen der Geraden und der Ebene beträgt rund .
Schnittwinkel zwischen zwei Ebenen
Zwei Ebenen schneiden sich, solange sie nicht echt parallel sind.
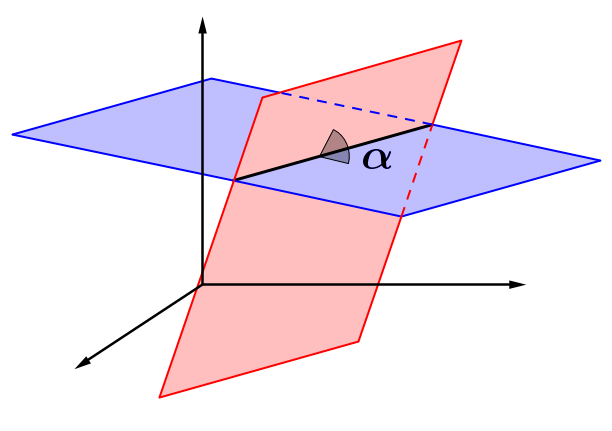
Seien die Normalenvektoren der Ebenen.
Dann lässt sich der Schnittwinkel so berechnen:
Beispiel
Gegeben sind zwei sich schneidende Ebenen und . Berechne den Schnittwinkel .
Für die Winkelberechnung zwischen zwei Ebenen benötigst du von den Ebenen deren Normalenvektoren und deren Beträge.
Lies die Normalenvektoren aus den Koordinatengleichungen ab:
und
Für den Betrag von gilt:
Für den Betrag von gilt:
Setze in die oben genannte Formel ein:
| ↓ | Setze die Vektoren und ihre Beträge ein. | ||
| ↓ | Berechne das Skalarprodukt und vereinfache. | ||
| ↓ | Vereinfache. | ||
| ↓ | Berechne den Betrag. | ||
Du hast die Gleichung erhalten. Durch Anwendung der Umkehrfunktion des Kosinus kannst du den Winkel berechnen. Benutze auf dem Taschenrechner die Funktion .
Antwort: Der Schnittwinkel zwischen den beiden Ebenen beträgt .
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
