Aufgaben zum Parallelogramm
Wiederhole Grundlagen zum Parallelogramm mit diesen Aufgaben. Hier lernst du, Parallelogramme zu erkennen, fehlende Seiten und andere Größen zu berechnen.
- 1
Berechne das Gesuchte im gegebenen Parallelogramm.
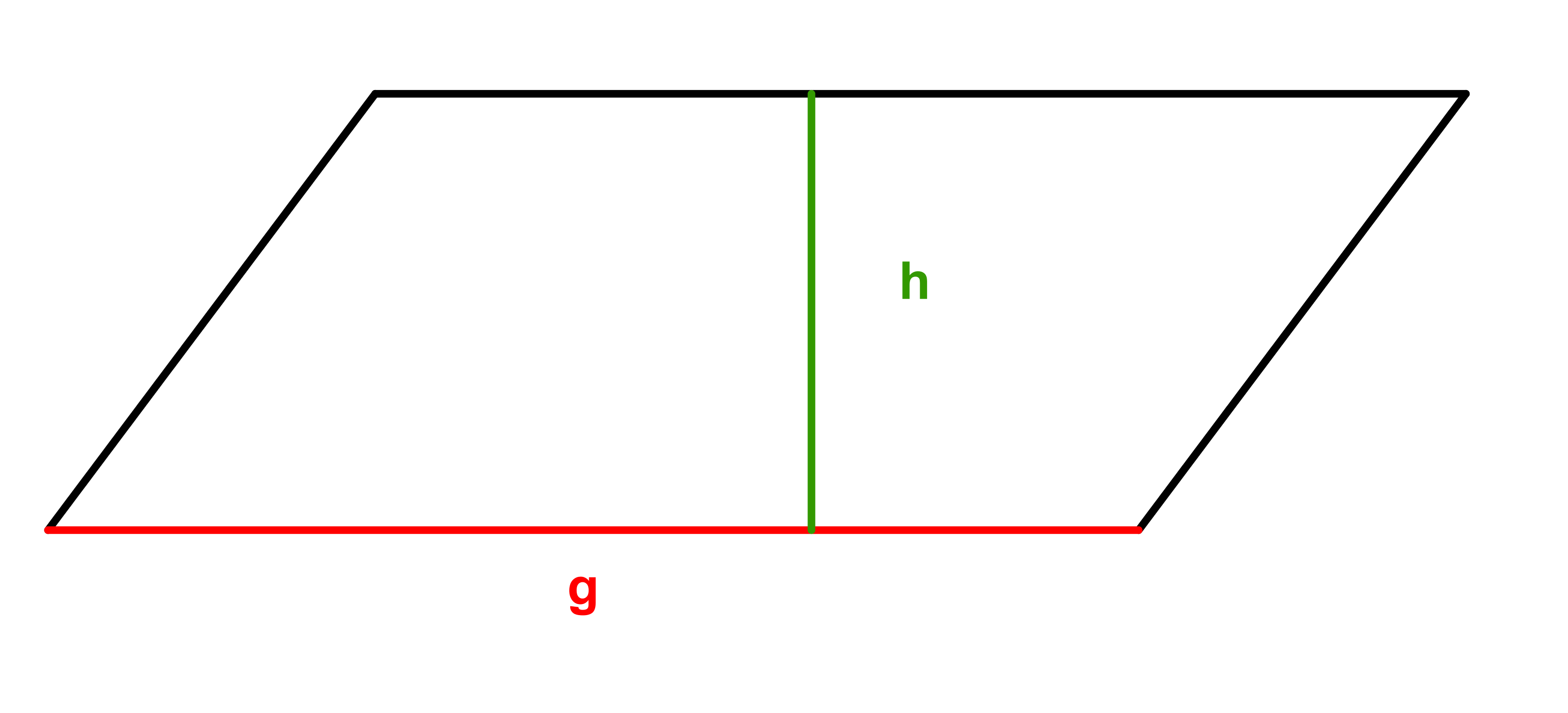
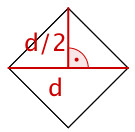
Gegeben ist die Höhe und der Flächeninhalt . Berechne die Grundlinie .
cmGegeben ist der Flächeninhalt und die Grundlinie . Berechne die Höhe .
cmGegeben ist die Grundlinie und die Höhe . Berechne den Flächeninhalt .
cm²Gegeben ist die Höhe und die Grundlinie . Berechne den Flächeninhalt .
cm²
- 2
Berechne die fehlenden Maße eines Parallelogramms.
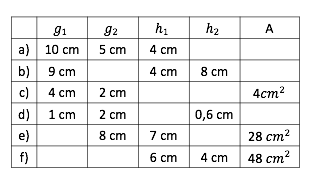
Gegeben:
gesucht:
Gegeben:
gesucht:
Gegeben:
gesucht:
Gegeben:
gesucht:
Gegeben:
gesucht:
Gegeben:
gesucht:
- 3
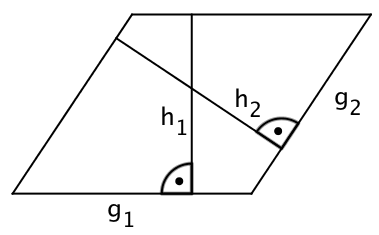
Wie viele Parallelogramme erkennst du in der gezeichneten Figur?
- 4
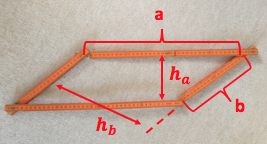
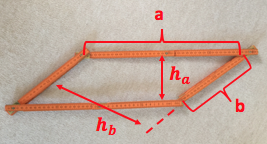
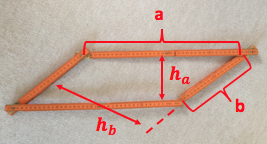
Experimentiere mit einem Zollstock
Mit einem Zollstock lassen sich leicht verschiedene Parallelogramme formen.

Durch die Seitenlängen (und somit auch durch seinen "Umfang", d.h. die Summe der Seitenlängen) ist die Form eines Parallelogramms nicht bestimmt. Zeige dies!
Welche Form besitzt ein Parallelogramm mit vorgegebenen Seitenlängen, wenn seine beiden Höhen am größten sind?
Was passiert mit der Höhe eines bestimmten "Zollstockparallelogramms", wenn man dieses ohne Veränderung der Seitenlängen so verbiegt, dass die Höhe nur noch die Hälfte (den dritten Teil; den vierten Teil) beträgt?
Wahr oder falsch?
Wird ohne Veränderung der Seitenlängen eine Höhe eines Parallelogramms um (, ) kleiner, dann wird auch die andere Höhe um (, ) kleiner.
- 5
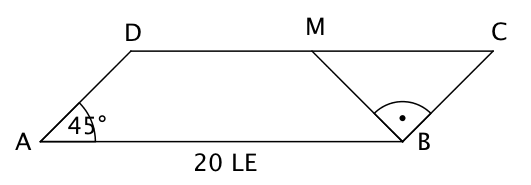
Schiebetüren:
Erkläre den Mechanismus des gezeichneten Schiebetürenmodells.
Wie groß ist die Breite der Türöffnung?
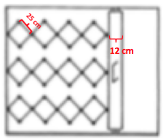 m ist die Breite der Türöffnung.
m ist die Breite der Türöffnung. - 6
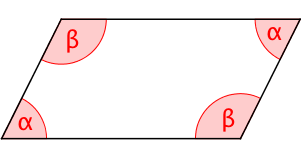
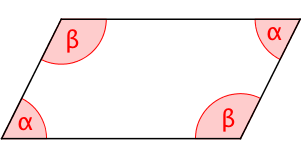
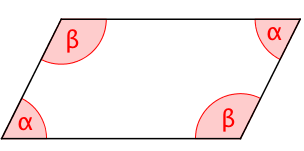
Berechne die Winkel eines Parallelogramms.
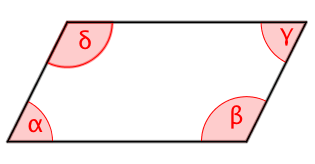
wenn einer der vier Winkel beträgt.
wenn die größeren Winkel gerade doppelt so groß sind wie die Kleineren.
wenn die kleineren Winkel um jeweils kleiner sind als die Größeren.
- 7
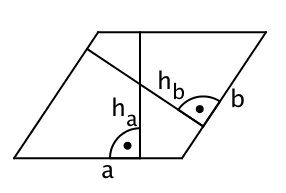
Berechne den Flächeninhalt des Parallelogramms.
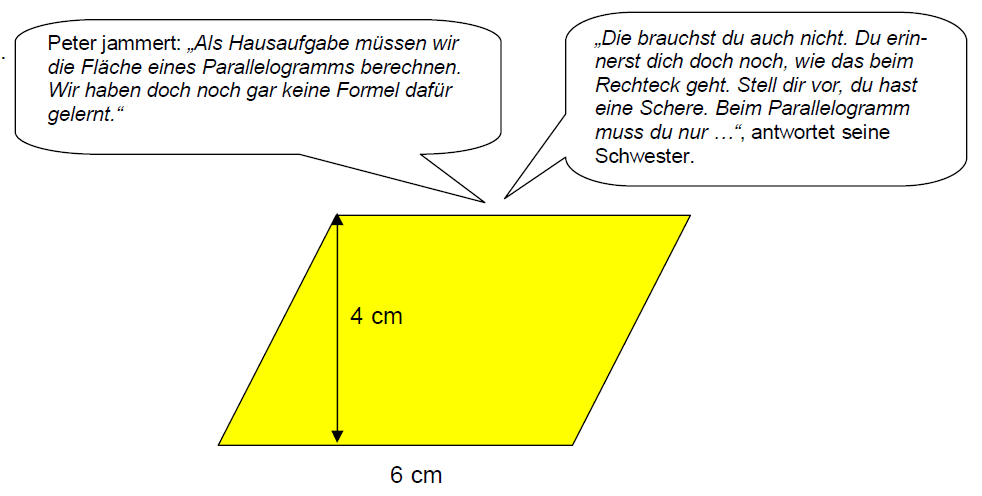 cm²
cm² - 8
Ein Parallelogramm hat den Flächeninhalt und die Höhe . Der Umfang des Parallelogramms beträgt Berechne die Seitenlängen und und die Höhe .
- 9
Parallelogramme lassen sich mit anderen Vierecken zu vielfältigen Formen zusammensetzen.
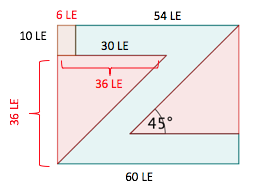
Berechne die Flächeninhalte der angegebenen Buchstaben-Formen.
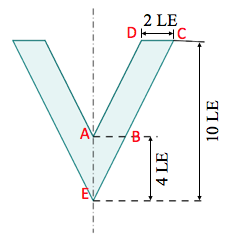
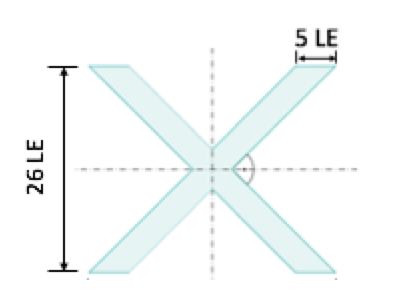
Berechne die gezeichnete Fläche.
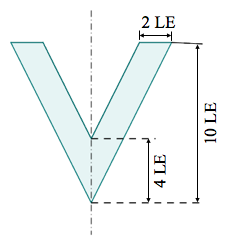 cm²
cm²Berechne die gezeichnete Fläche.
 FE
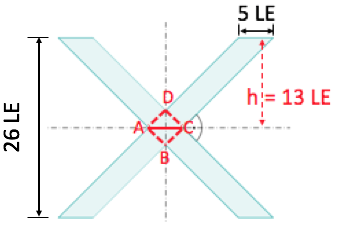
FEBerechne die gezeichnete Fläche.
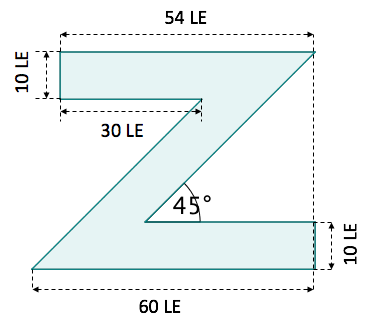 FE
FE
- 10
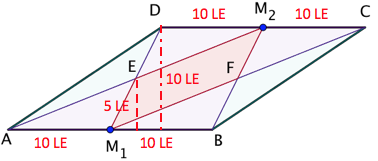
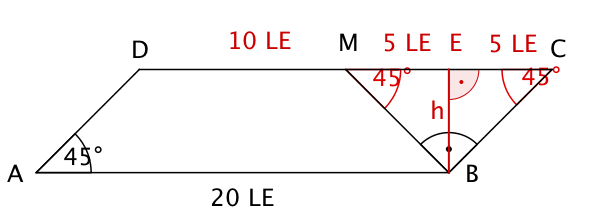
Parkettierung eines Parallelogramms
Unter einer Parkettierung einer geometrischen Figur versteht man die vollständige überschneidungsfreie Überdeckung der Figur mit Teilfiguren.
Für das gezeichnete Parallelogramm gelte , die zugehörige Höhe betrage . und seien Mittelpunkte der Parallelogrammseiten.
Berechne die Flächeninhalte der überdeckenden Teilfiguren.
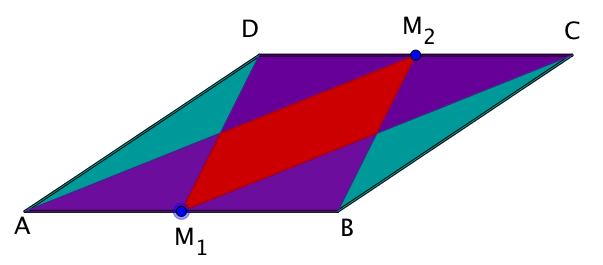
- 11
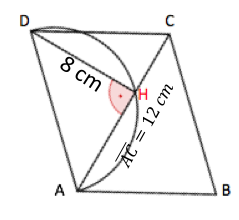
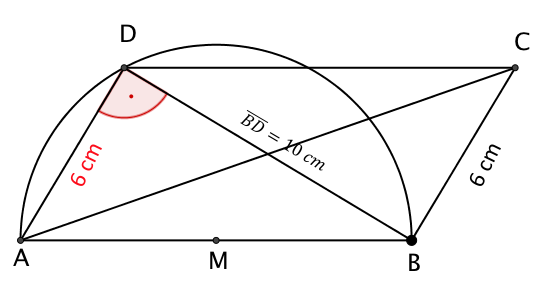
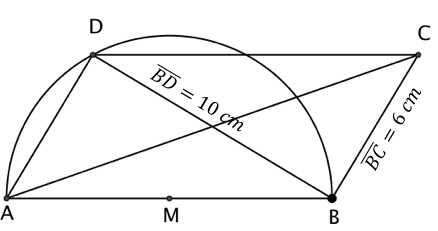
Berechne die Flächeninhalte der Parallelogramme .
Berechne den Flächeninhalt des Parallelogramms , wobei den Durchmesser des Kreises bildet.
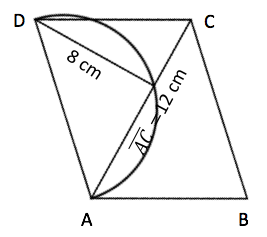 cm²
cm²Berechne den Flächeninhalt des Parallelogramms , wobei den Durchmesser des Kreises bildet.
 cm²
cm²Berechne den Flächeninhalt des Parallelogramms , wenn der Mittelpunkt von ist.
 FE
FE
- 12
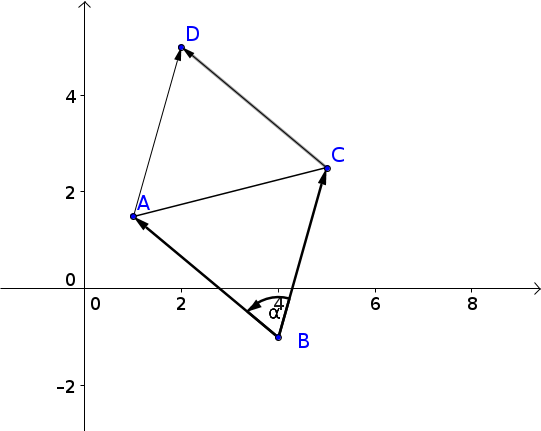
Berechne die Fläche des Parallelogramms, das von den angegebenen Punkten aufgespannt wird.
- FE
- 13
Wie unterscheiden sich Flächeninhalt und Umfang der beiden abgebildeten Vierecke?
Du musst die Fläche und den Umfang für deine Antwort nicht berechnen!
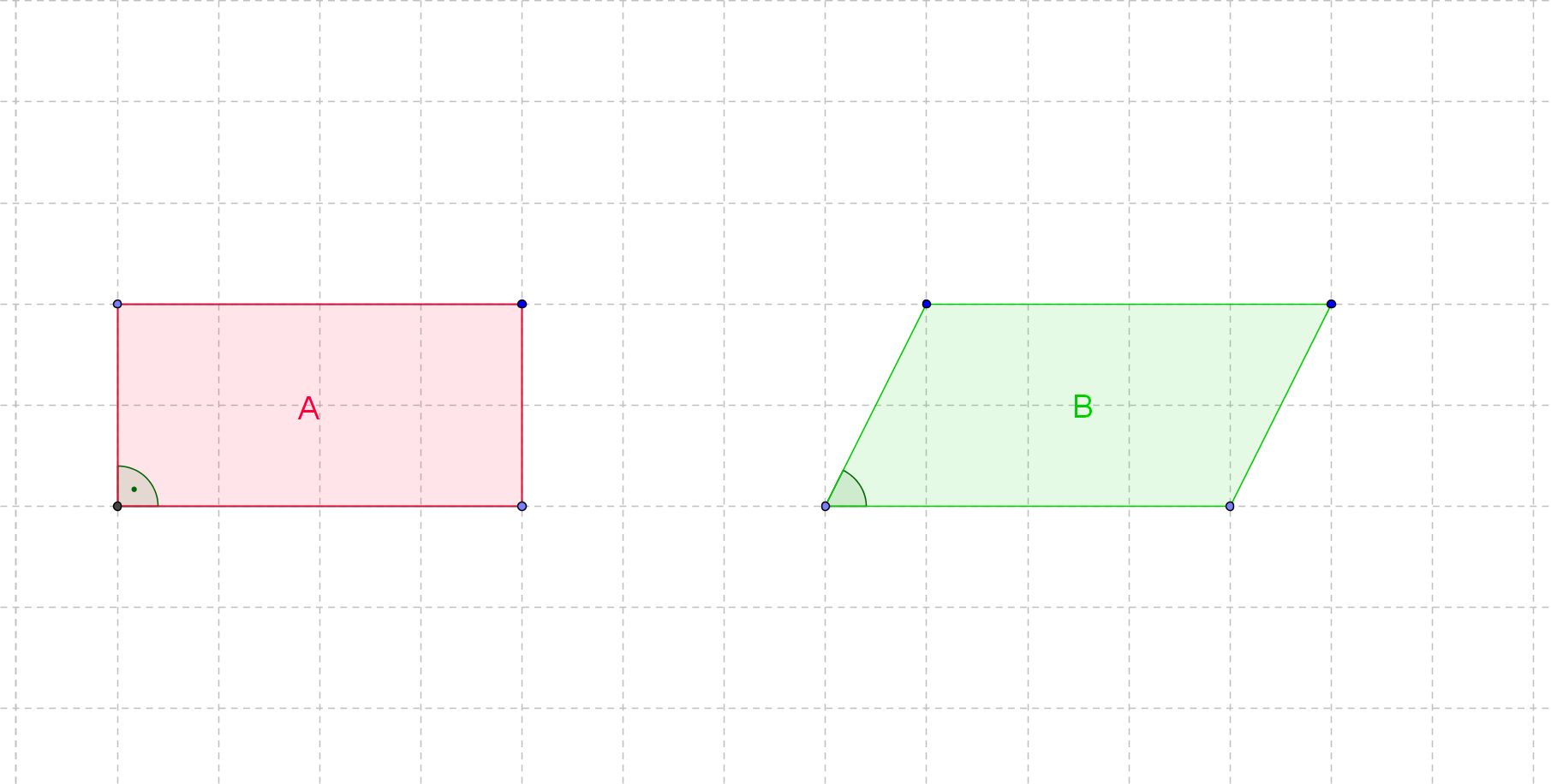
Klicke von den folgenden Antworten alle richtigen an:
- 14
Löse folgende Aufgaben:
„Jedes Trapez ist ein halbes Parallelogramm!“
Veranschauliche diese Aussage, indem du das Trapez in obiger Zeichnung geeignet ergänzt.
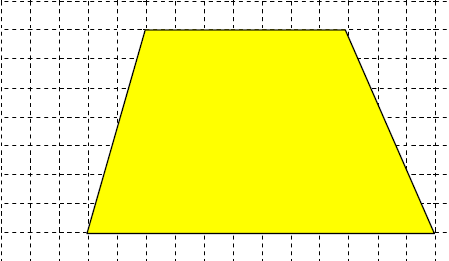
Berechne den Flächeninhalt des gelben Trapezes.
FE (Flächeneinheiten)„Jedes Dreieck ist ein halbes Parallelogramm!“
Veranschauliche diese Aussage, indem du das Dreieck in obiger Zeichnung geeignet ergänzt.
Berechne den Flächeninhalt des roten Dreiecks.
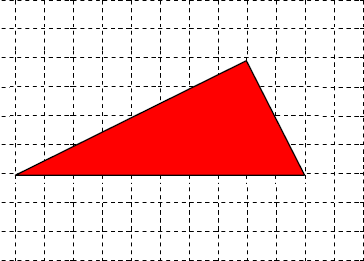 FE
FE
- 15
Parallelogramm: Ziehe die Wörter in die passenden Lücken.
- 16
Welcher der Parallelogramme haben einen Umfang von ?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?