Ein Parallelogramm ist
ein Viereck, in dem
gegenüberliegende Seiten parallel zueinander sind.
Ein Parallelogramm kann man auch als punktsymmetrisches Viereck definieren:
Jedes Parallelogramm ist punktsymmetrisch.
Symmetriepunkt ist immer der Schnittpunkt der beiden Diagonalen.
… und umgekehrt gilt auch:
Wenn ein Viereck punktsymmetrisch ist, dann ist es ein Parallelogramm.
Eigenschaften des Parallelogramms
Besonderheiten bei Seiten, Winkeln und Diagonalen
In einem Parallelogramm sind
gegenüberliegende Seiten immer gleich lang.
Im Parallelogramm gilt also:

In einem Parallelogramm
sind gegenüberliegende Winkel immer gleich groß. Im Parallelogramm gilt also:
ergeben zwei auf derselben Seite liegende Winkel zusammen immer 180°.
In einem Parallelogramm
halbieren sich die Diagonalen gegenseitig.
Einordnung als Viereck
Jedes Parallelogramm ist immer auch ein Trapez, und zwar ein (besonderes) Trapez, bei dem nicht nur ein Paar gegenüberliegender Seiten parallel ist, sondern beide Paare.
Wie sich das Parallelogramm im Vergleich zu allen anderen Vierecken einordnen lässt, kannst du auch im Haus der Vierecke sehen.
Spezialfälle von Parallelogrammen
Wenn ein Parallelogramm vier rechte Winkel hat, ist es ein Rechteck.
Wenn ein Parallelogramm vier gleich lange Seiten hat, ist es eine Raute.
Wenn ein Parallelogramm vier rechte Winkel und außerdem vier gleich lange Seiten hat, ist es ein Quadrat.
Symmetrieeigenschaften
Punktsymmetrie
Jedes Parallelogramm ist punktsymmetrisch zum Schnittpunkt seiner Diagonalen (und ein punktsymmetrisches Viereck ist automatisch immer ein Parallelogramm).
Achsensymmetrie
Ein Parallelogramm ist im Allgemeinen nicht achsensymmetrisch, hat also keine Symmetrieachse.
Ausnahmen:
Wenn ein Parallelogramm eine Raute ist, ist es achsensymmetrisch zu jeder der beiden Diagonalen.
Wenn ein Parallelogramm ein Rechteck ist, ist es achsensymmetrisch zu jeder der beiden Mittelparallelen.
Umkreis und Inkreis
Ein Parallelogramm hat im Allgemeinen weder einen Umkreis noch einen Inkreis.
Ausnahmen:
Umkreis: Wenn ein Parallelogramm ein Rechteck ist, hat es einen Umkreis. Und umgekehrt: Ein Parallelogramm, das einen Umkreis hat, ist immer ein Rechteck.
Inkreis: Wenn ein Parallelogramm eine Raute ist, hat es einen Inkreis. Und umgekehrt: Ein Parallelogramm, das einen Inkreis hat, ist immer eine Raute.
Flächeninhalt und Umfang
Flächeninhalt
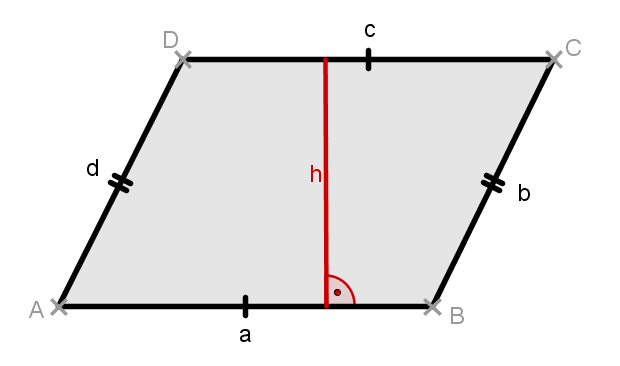
Der Flächeninhalt eines Parallelogramms ist das Produkt aus Höhe und Seitenlänge:
Eine anschauliche Herleitung der Formel erhält man im folgenden Applet:
Video zur Flächenformel für das Parallelogramm
Laden
Umfang
Der Umfang eines Parallelogramms ist die Summe der Seitenlängen. Da jeweils zwei Seiten die gleiche Länge haben, ist der Umfang gegeben durch
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Parallelogramm
