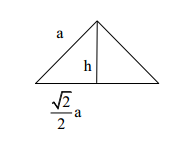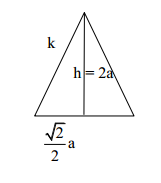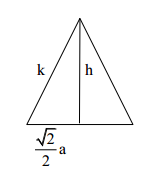Schwierigere Aufgaben zu einzelnen Grundkörpern
Du suchst die Herausforderung? Hier findest du sie mit schwierigeren Aufgaben zu verschiedenen Grundkörpern.
- 1
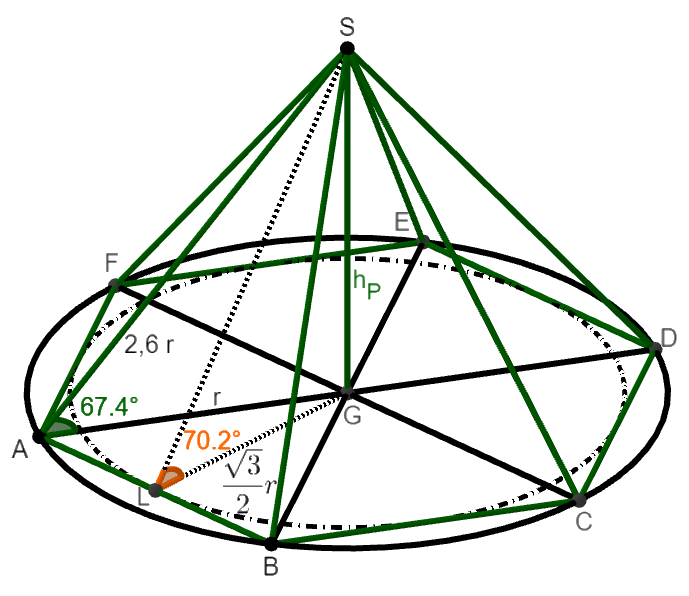
Eine Pyramide habe als Grundfläche ein regelmäßiges Sechseck mit Umkreisradius ( Grundkantenlänge auch und der Inkreisradius ist ).
Der Höhenfußpunkt der Pyramide ist der Umkreismittelpunkt, die Seitenkantenlänge ist .
Berechne das Volumen der Pyramide.
Berechne den Neigungswinkel der Seitenkante zur Grundfläche und den Neigungswinkel der Seitenfläche zur Grundfläche.
- 2
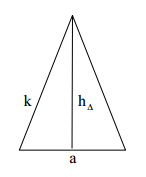
Eine gerade Pyramide hat als Grundfläche ein gleichseitiges Dreieck mit der Kantenlänge a. Die Höhe der Pyramide beträgt 2a. Berechne die Seitenkantenlängen in Vielfachen von a. Berechne den Oberflächeninhalt der Pyramide in Vielfachen von a.
- 3
Eine gerade Pyramide hat als Grundfläche ein Rechteck mit den Seitenlängen und . Die Höhe der Pyramide beträgt .
Berechne die Kantenlängen als Vielfache von .
Berechne den Oberflächeninhalt der Pyramide in Vielfachen von .
- 4
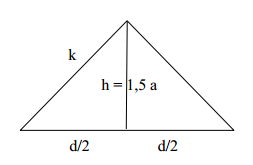
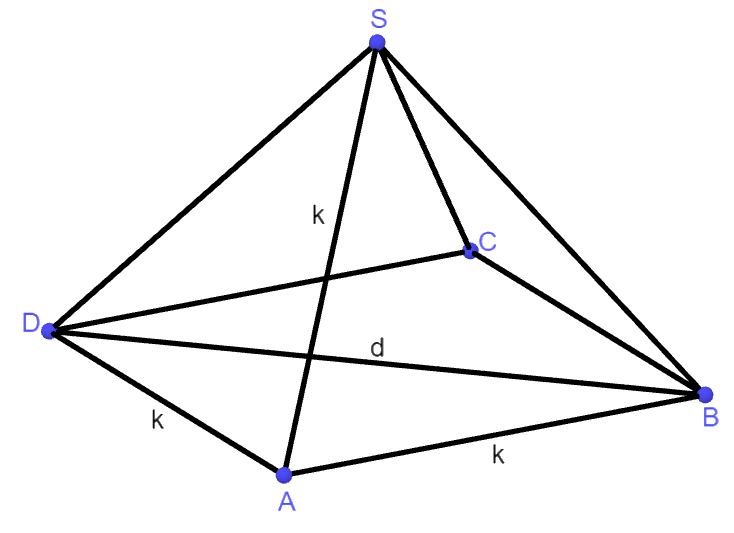
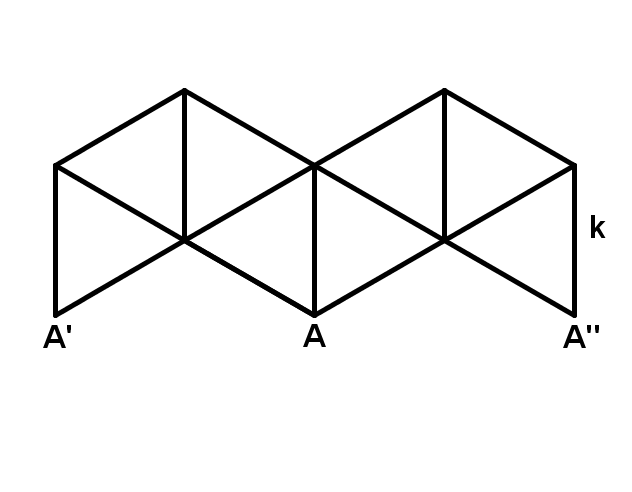
Das nebenstehende Netz mit lauter gleichseitigen Dreiecken mit Seitenlänge k lässt sich zu einem Oktaeder falten, indem man zunächst aus der "linken" Hälfte des Netzes eine Pyramide herstellt.
Berechne die Höhe dieser Pyramide und zeichne ein Schrägbild des Oktaeders.
- 5
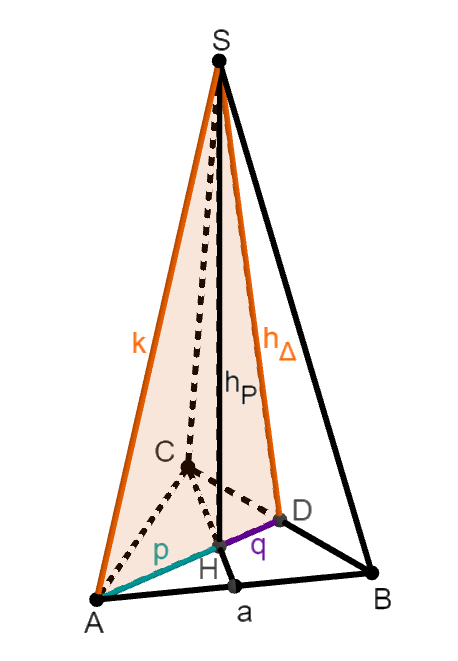
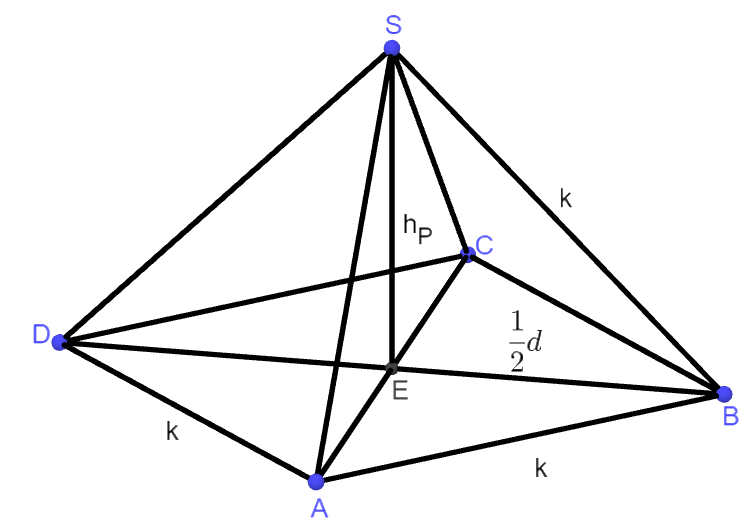
Das Bild zeigt eine gerade Pyramide mit einem Quadrat als Grundfläche. Der Punkt halbiert die Höhe .
Die Winkel im Dreieck hängen nicht von ab.
Berechne jeweils in Abhängigkeit von
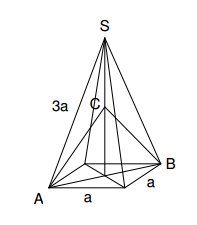
Das Volumen der Pyramide
Den Oberflächeninhalt der Pyramide
Die drei Seitenlängen im Dreieck .
Die Winkel im Dreieck .
Den Flächeninhalt des Dreiecks .
- 6
Das Bild zeigt eine gerade Pyramide mit einem Quadrat der Kantenlänge als Grundfläche. Die Seitenkanten haben ebenfalls die Länge .
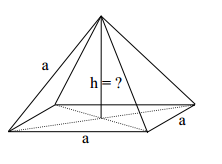
Zeichne ein Netz der Pyramide für .
Berechne die Höhe der Pyramide in Vielfachen von .
Berechne den Oberflächeninhalt der Pyramide
- 7
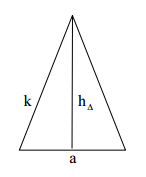
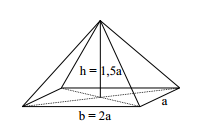
Das Bild zeigt eine gerade Pyramide mit einem Quadrat der Kantenlänge als Grundfläche. Die Höhe der Pyramide ist .
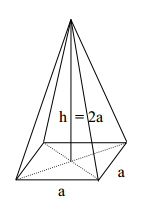
Berechne die Länge der Seitenkanten in Vielfachen von .
Berechne den Oberflächeninhalt der Pyramide in Vielfachen von .
Bestimme auf Millimeter genau, wenn der Oberflächeninhalt genau betragen soll.
- 8
Ein Würfel und eine gerade Pyramide haben jeweils ein Quadrat der Kantenlänge als Grundfläche. Beide Körper sollen den gleichen Oberflächeninhalt haben.
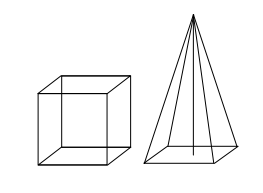
Wie lang müssen dann die Seitenkanten der Pyramide sein?
Berechne auch die Höhe der Pyramide.
- 9
Das Bild zeigt eine gerade Pyramide mit einem Quadrat als Grundfläche. Der Punkt halbiert die Höhe .
Die Winkel im Dreieck hängen nicht von ab.
Berechne jeweils in Abhängigkeit von
Das Volumen der Pyramide
Den Oberflächeninhalt der Pyramide
Die drei Seitenlängen im Dreieck
Die Winkel im Dreieck
Den Flächeninhalt des Dreiecks
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?