Beim Klammern ausmultiplizieren geht es darum, die Klammern aufzulösen und dadurch den Term umzuschreiben.
Wenn ein Term
multipliziert werden soll,
muss
jeder Summand bzw. Minuend und Subtrahend
mit diesem Term multipliziert werden,
um die Klammer ganz ausmultiplizieren.
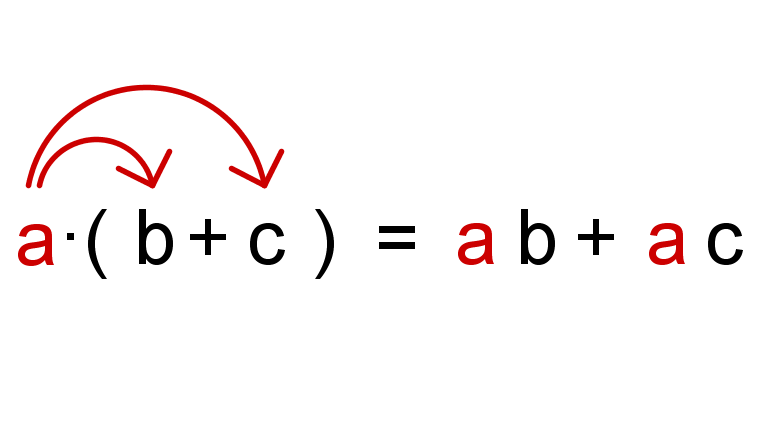
Faktor mal Klammer
Jedes Glied der Summe bzw. Differenz in der Klammer muss mit dem Faktor vor (oder hinter!) der Klammer multipliziert werden:
Wenn eine Zahl mit einer Klammer, in der eine Summe oder Differenz steht, multipliziert werden soll, muss jeder Summand bzw. sowohl der Minuend als auch der Subtrahend mit dieser Zahl multipliziert werden.
Entsprechend geht man vor, wenn eine Variable oder ein längerer Term mit einer solchen Klammer multipliziert werden soll.
Beispiele

Graphik: Ausmultiplizieren einer Klammer "Jeder Summand bekommt den Faktor ab."
Klammer mal Klammer
Wenn der Term, mit dem die Klammer multipliziert werden soll, selbst eine Klammer mit einer Summe oder Differenz ist, muss jedes Glied der ersten Summe bzw. Differenz mit jedem Glied der zweiten Summe bzw. Differenz multipliziert werden.
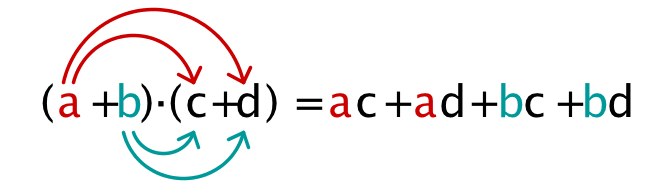
Graphik: Ausmultiplizieren zweier Klammern "Jeder aus der ersten Klammer mit jedem aus der zweiten Klammer"
Du kannst dir einen noch besseren Überblick über die Rechnung verschaffen, wenn du die Tabellenmethode anwendest.
Beispiel
Wenn dieselbe Klammer mit sich selbst multipliziert wird, z.B. , oder ein Term der Form auftritt, kannst du dir die Arbeit vereinfachen, indem du die binomischen Formeln verwendest.
Produkt in der Klammer
Wenn in der Klammer ein Produkt steht (statt einer Summe oder Differenz), darf man nicht jeden Faktor des Produkts in der Klammer mit dem Faktor vor der Klammer multiplizieren, sondern nur einen (egal welchen).
Die Klammer kann man laut Assoziativgesetz weglassen, die Faktoren laut Kommutativgesetz vertauschen.
Beispiele:
, aber
oder auch:
Video zum Thema Ausmultiplizieren und Ausklammern
Laden
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Ausmultiplizieren
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
