Berechne für folgende Parabel die Scheitelpunktform und den Scheitelpunkt. Zeichne den Graphen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Parabel
↓ ↓ In eine Binomische Formel umschreiben
↓ Scheitelpunkt ablesen.
Scheitelpunkt:
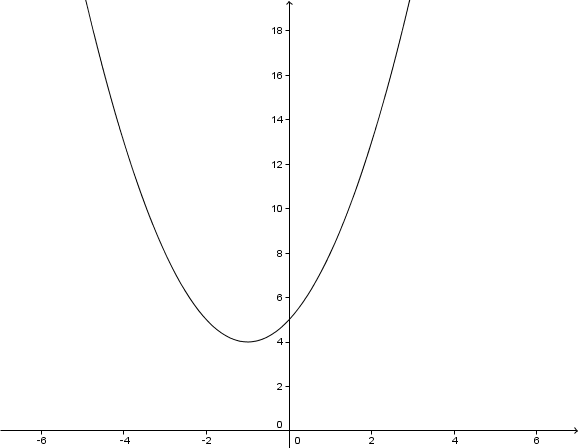
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform einer Parabel
↓ ↓ In eine Binomische Formel umschreiben.
↓ Scheitelpunkt ablesen
Scheitelpunkt:
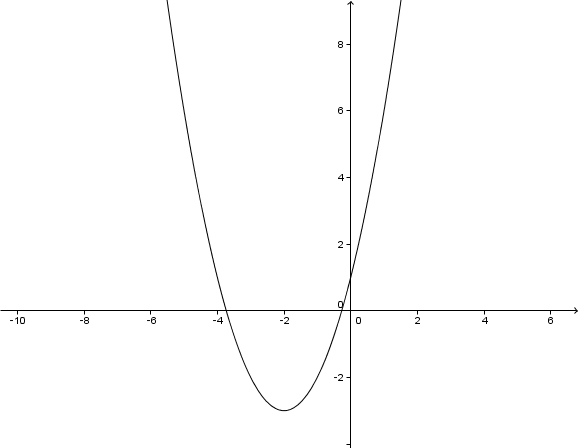
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform einer Parabel
↓ ↓ In eine Binomische Formel umschreiben.
↓ Scheitelpunkt ablesen.
Scheitelpunkt:
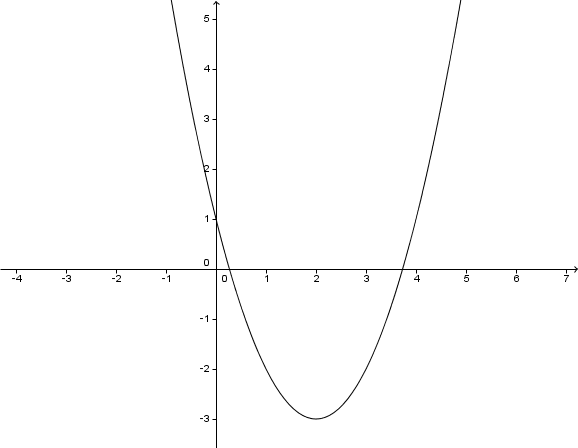
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform einer Parabel
↓ ↓ In eine binomische Formel umschreiben.
↓ ↓ Scheitelpunkt ablesen.
Scheitelpunkt:
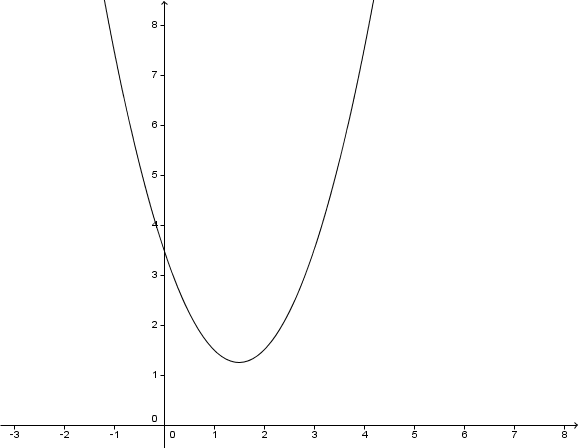
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform einer Parabel
↓ ↓ In eine Binomische Formel umschreiben.
↓ 3 in einen unechten Bruch umwandeln
↓ Scheitelpunkt ablesen.
Scheitelpunkt:
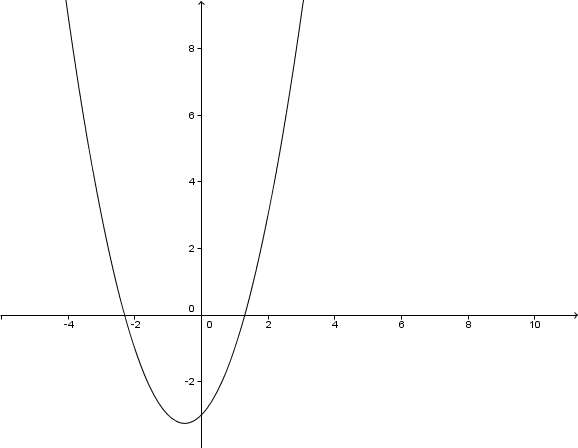
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform einer Parabel
↓ Distributivgesetz anwenden. Minus ausklammern.
↓ ↓ In eine Binomische Formel umschreiben.
↓ Distributivgesetz anwenden.
↓ Scheitelpunkt ablesen.
Scheitelpunkt:
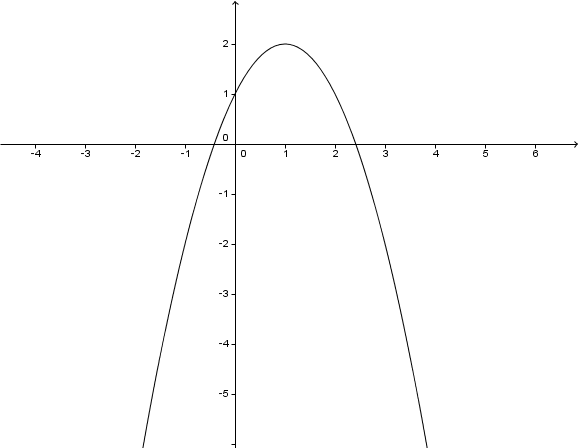
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform einer Parabel
↓ Distributivgesetz anwenden. Minus ausklammern.
↓ ↓ In eine Binomische Formel umschreiben.
↓ 5 in einen unechten Bruch umschreiben
↓ Distributivgesetz anwenden.
↓ Scheitelpunkt ablesen.
Scheitelpunkt:
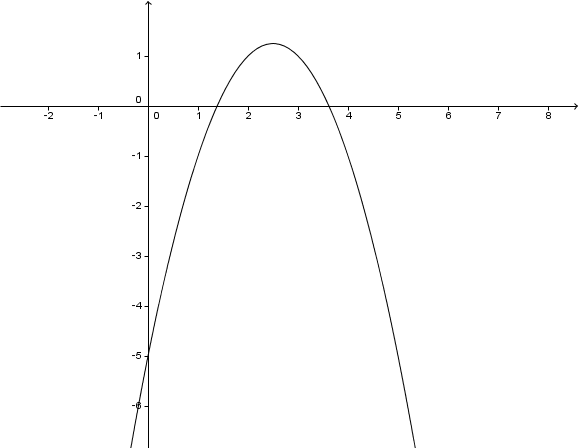
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform einer Parabel
↓ Distributivgesetz anweden. ausklammern.
↓ Mit dem Kehrwert multiplizieren.
↓ ↓ In eine Binomische Formel umschreiben.
↓ Distributivgesetz anweden.
↓ Scheitelpunkt ablesen
Scheitelpunkt:
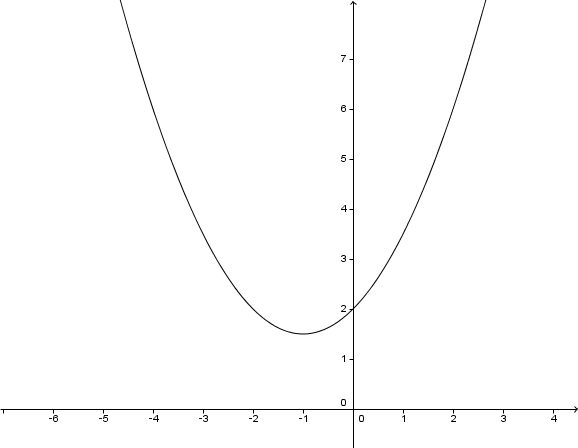
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform einer Parabel
↓ Distributivgesetz anwenden und ausklammern.
↓ ↓ In eine binomische Formel umschreiben.
↓ Gemeinsamen Hauptnenner bilden und auf diesen erweitern.
↓ Distributivgesetz anwenden.
↓ Mit 3 und 2 kürzen.
Jetzt kannst du den Scheitelpunkt ablesen.
Scheitelpunkt:
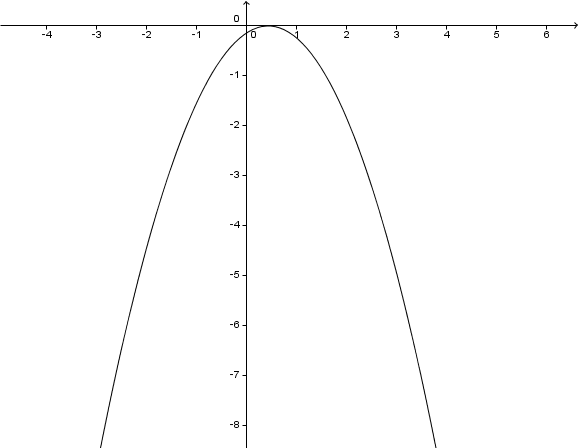
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform einer Parabel
↓ Distributivgesetz anweden. ausklammern.
↓ Mit dem Kehrwert multiplizieren.
↓ Jeweils mit 3 kürzen.
↓ ↓ In eine binomische Formel umschreiben.
↓ Distributivgesetz anwenden.
Nun kannst du den Scheitelpunkt ablesen.
Scheitelpunkt:
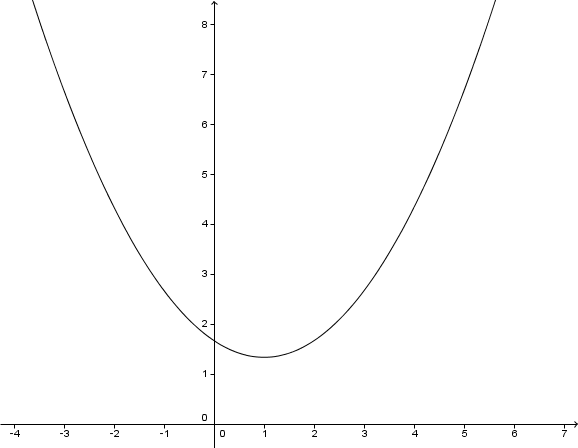
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann → Was bedeutet das?
