Elemente der Kurvendiskussion
Bestimmen Sie die Extrempunkte der Funktion mit
Bestimmen Sie den Wendepunkt der Funktion mit
Gegeben ist die Funktion mit
a) Bestimmen Sie die Gleichung der Normalen von im Punkt .
b) Bestimmen Sie den Schnittpunkt der Normalen mit der x-Achse.
Die Funktion hat das nebenstehende Schaubild und die Funktionsgleichung
,
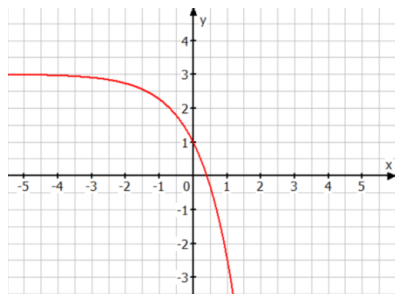
a) Bestimmen Sie die Werte von und .
b) Berechnen Sie, an welcher Stelle die Funktion die Steigung besitzt.
Gegeben sind die Funktionen und mit und .
Geben Sie die waagrechte Asymptote der Funktion an.
Bestimmen Sie die Stelle, an der und die gleiche Steigung haben.
Gegeben ist die Funktion mit
a) Skizzieren Sie das Schaubild von .
b) Berechnen Sie die Gleichung der Tangente an den Graphen von an der Stelle und zeichnen Sie die Tangente ein.
Gegeben ist die Funktion mit .
a) Berechnen Sie die Steigung von an der Stelle .
b) Berechnen Sie die Stelle, an der die Funktion die Steigung hat.
c) Bestimmen Sie die Gleichung der Tangente an der Stelle .
Gegeben ist die Funktion mit
a) Skizzieren Sie das Schaubild von für .
b) Bestimmen Sie die Steigung von an der Stelle .
c) Bestimmen Sie so, dass der Ursprung auf dem Schaubild von liegt.
Dieses Werk steht unter der freien Lizenz
CC BY 4.0 mit Namensnennung Landesbildungsserver Baden-Württemberg → Was bedeutet das?


