Aufgaben zu quadratischen Funktionen
- 1
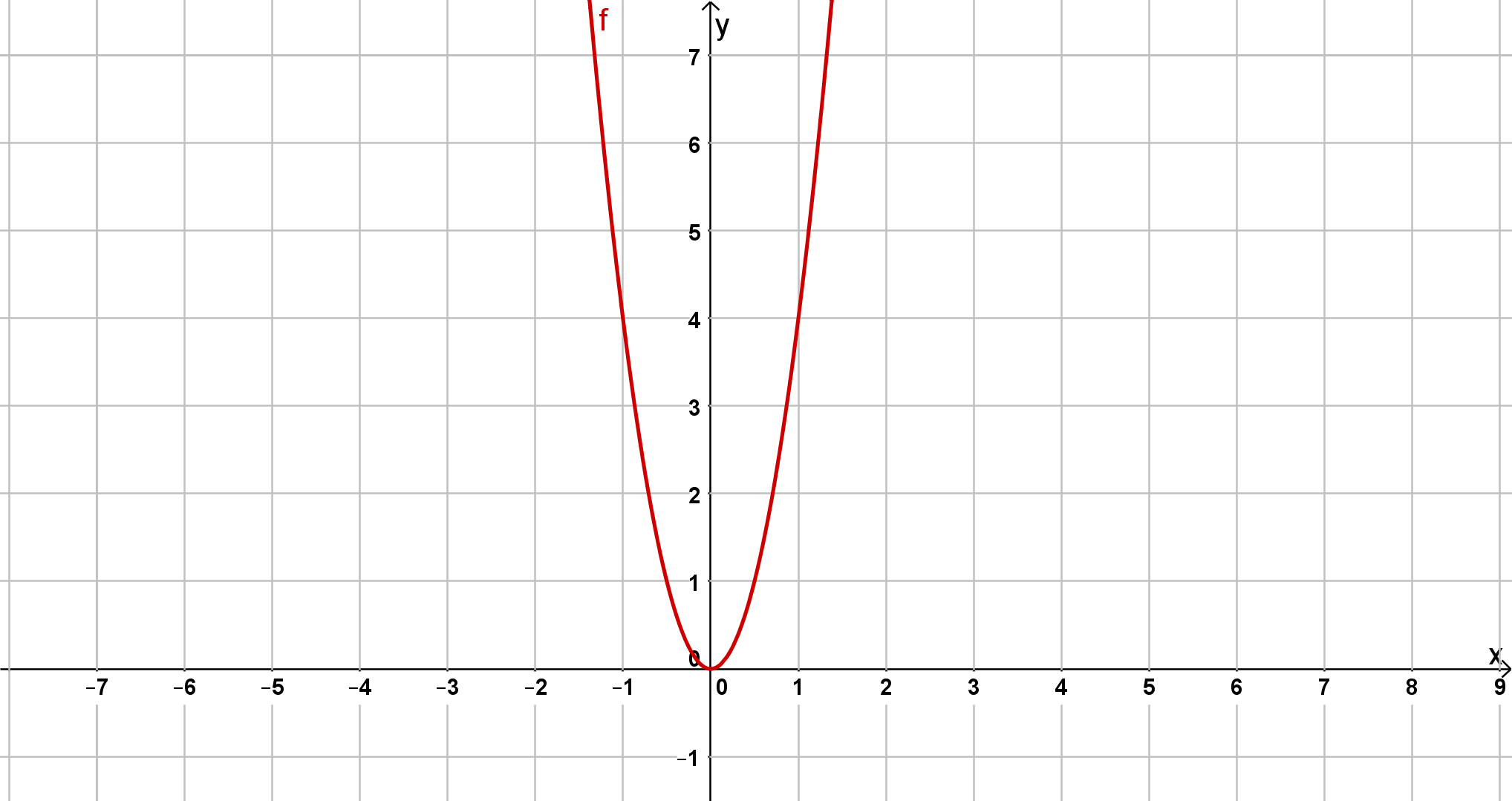
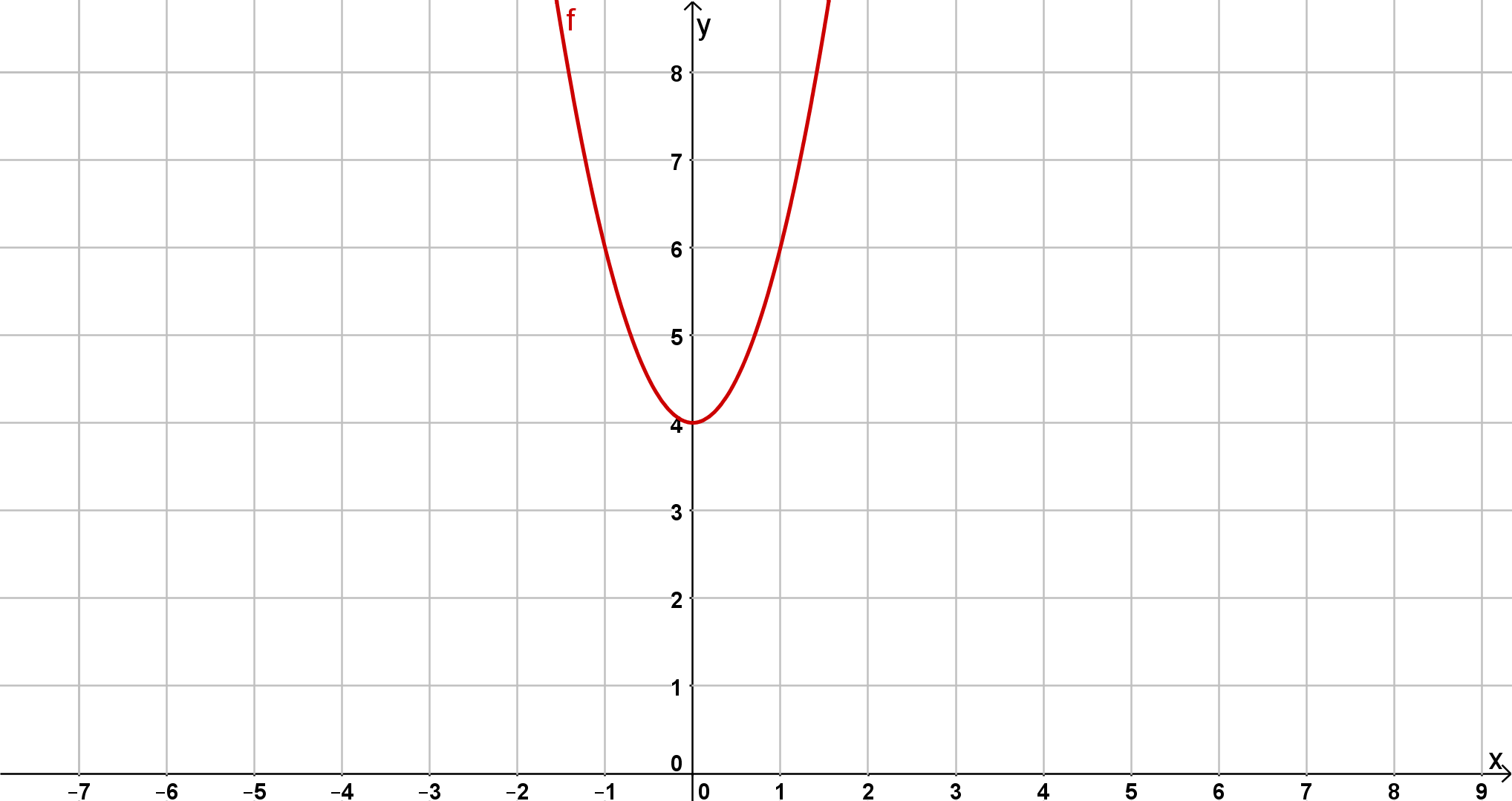
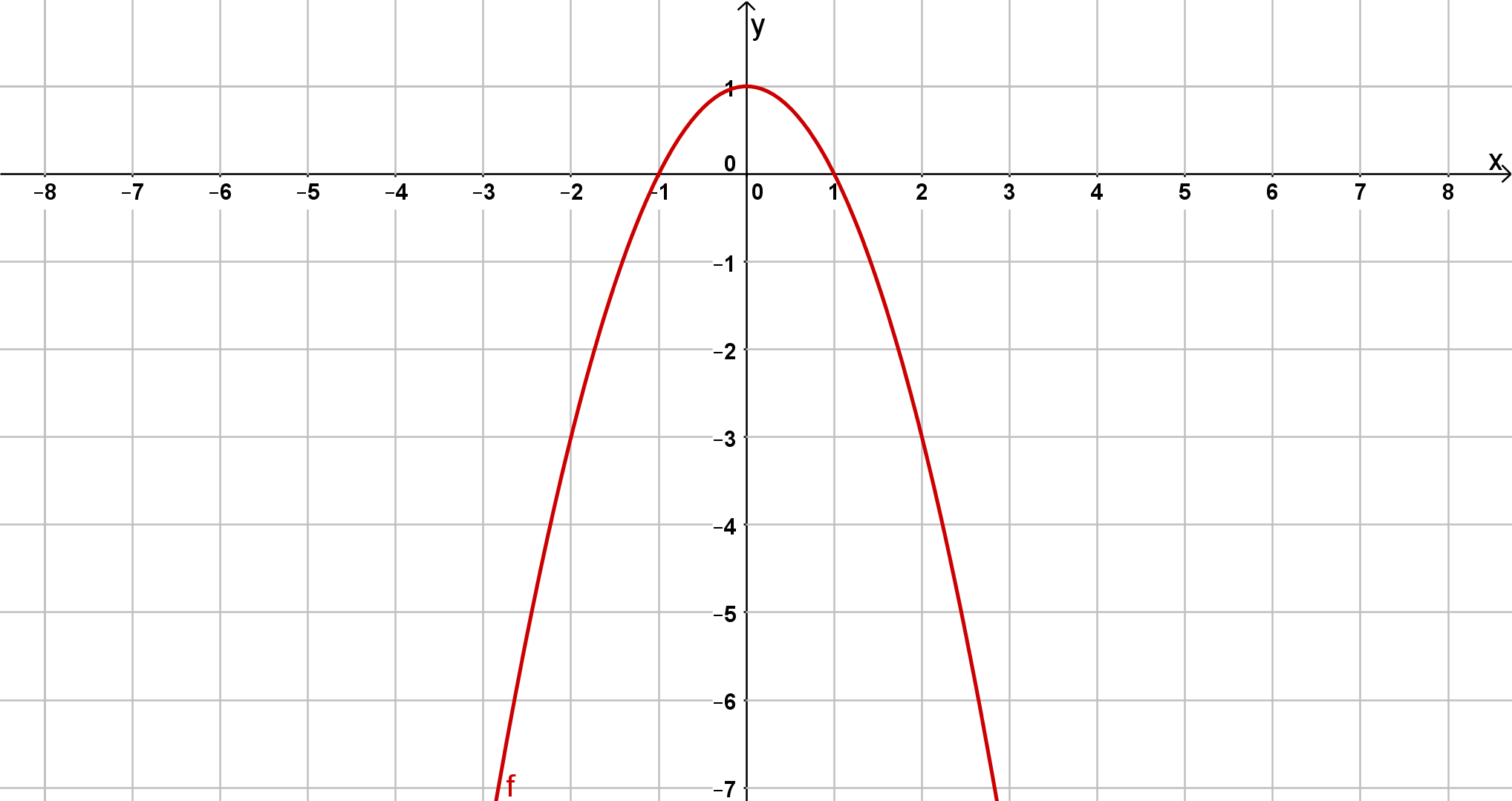
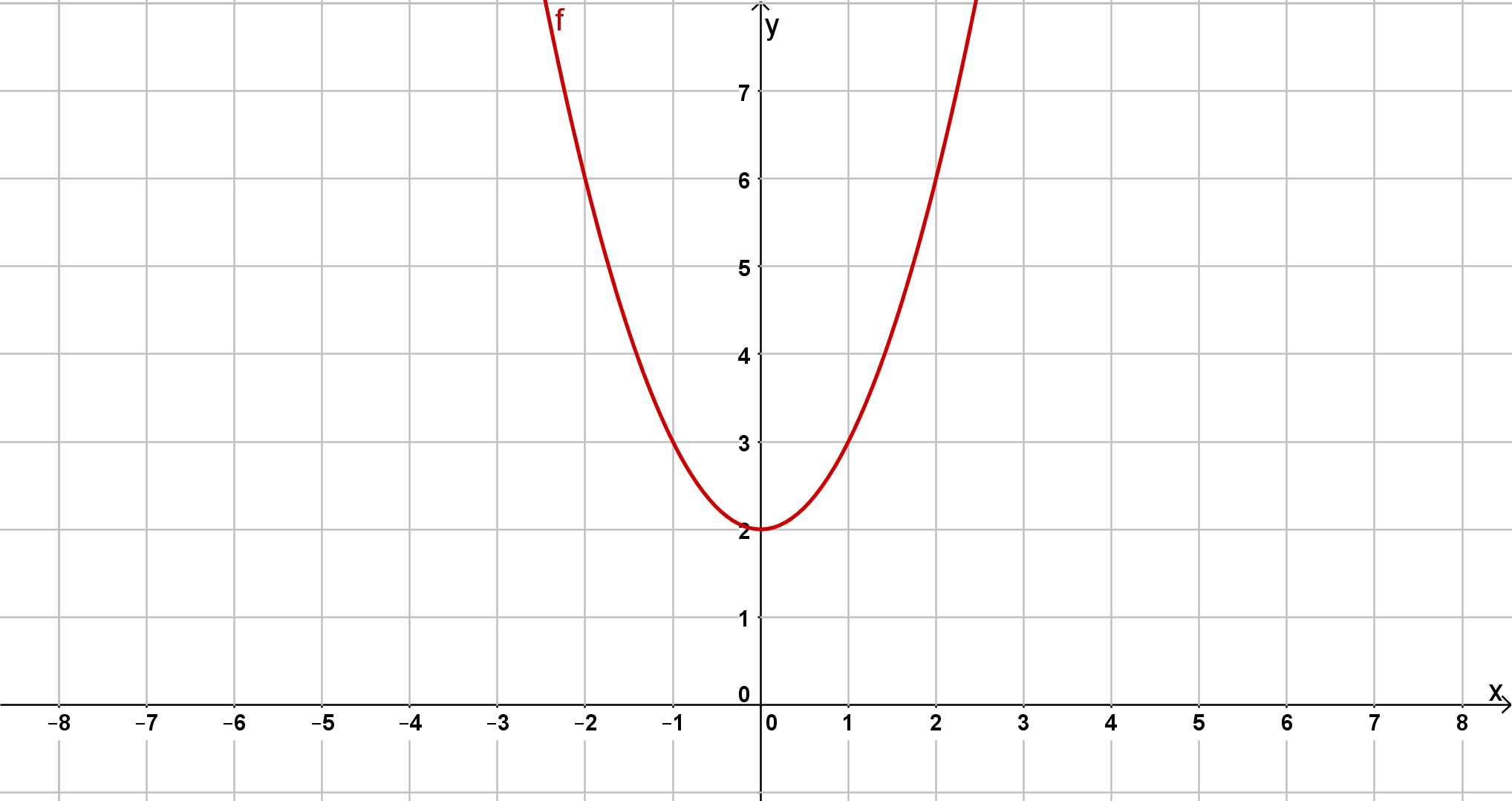
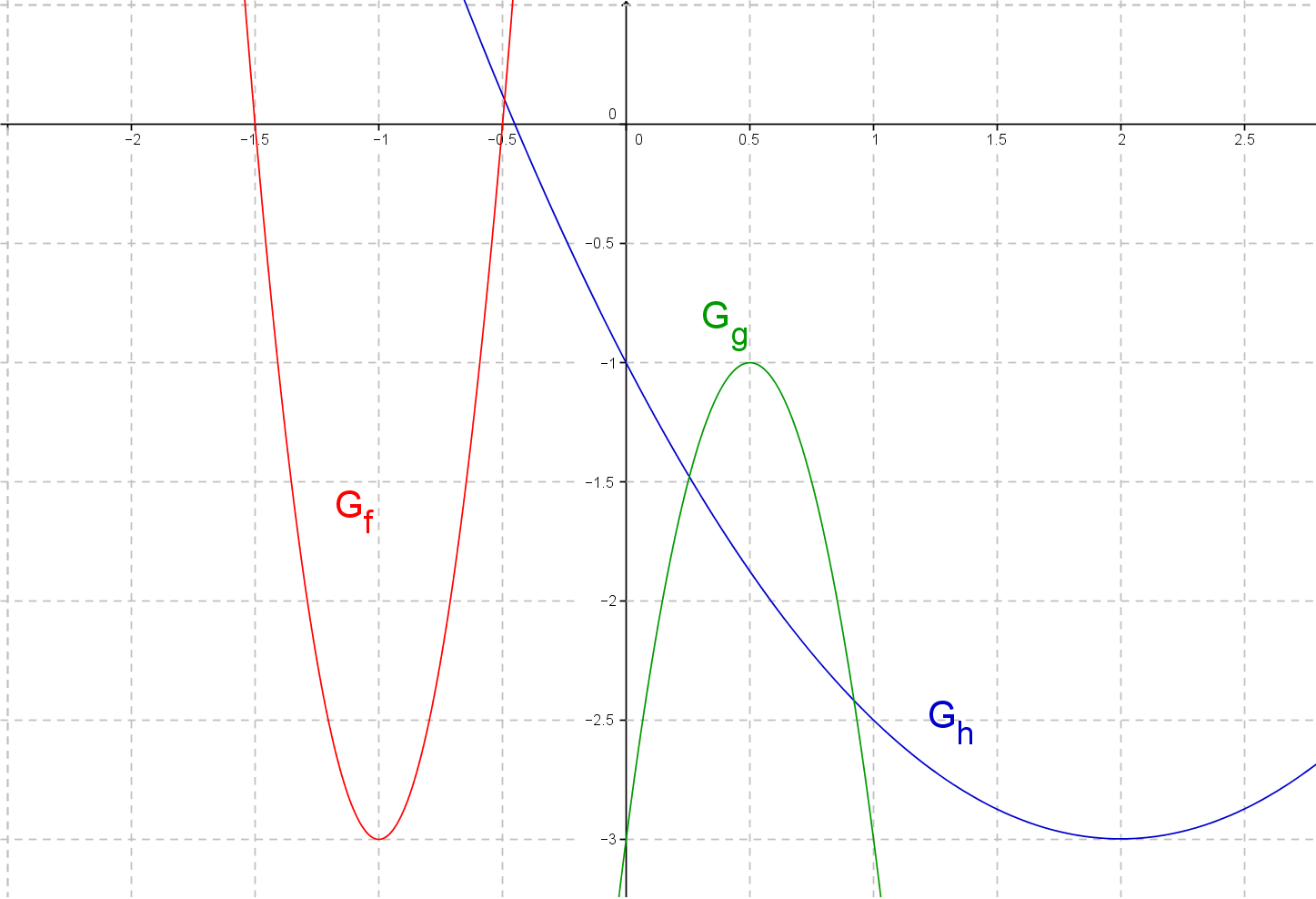
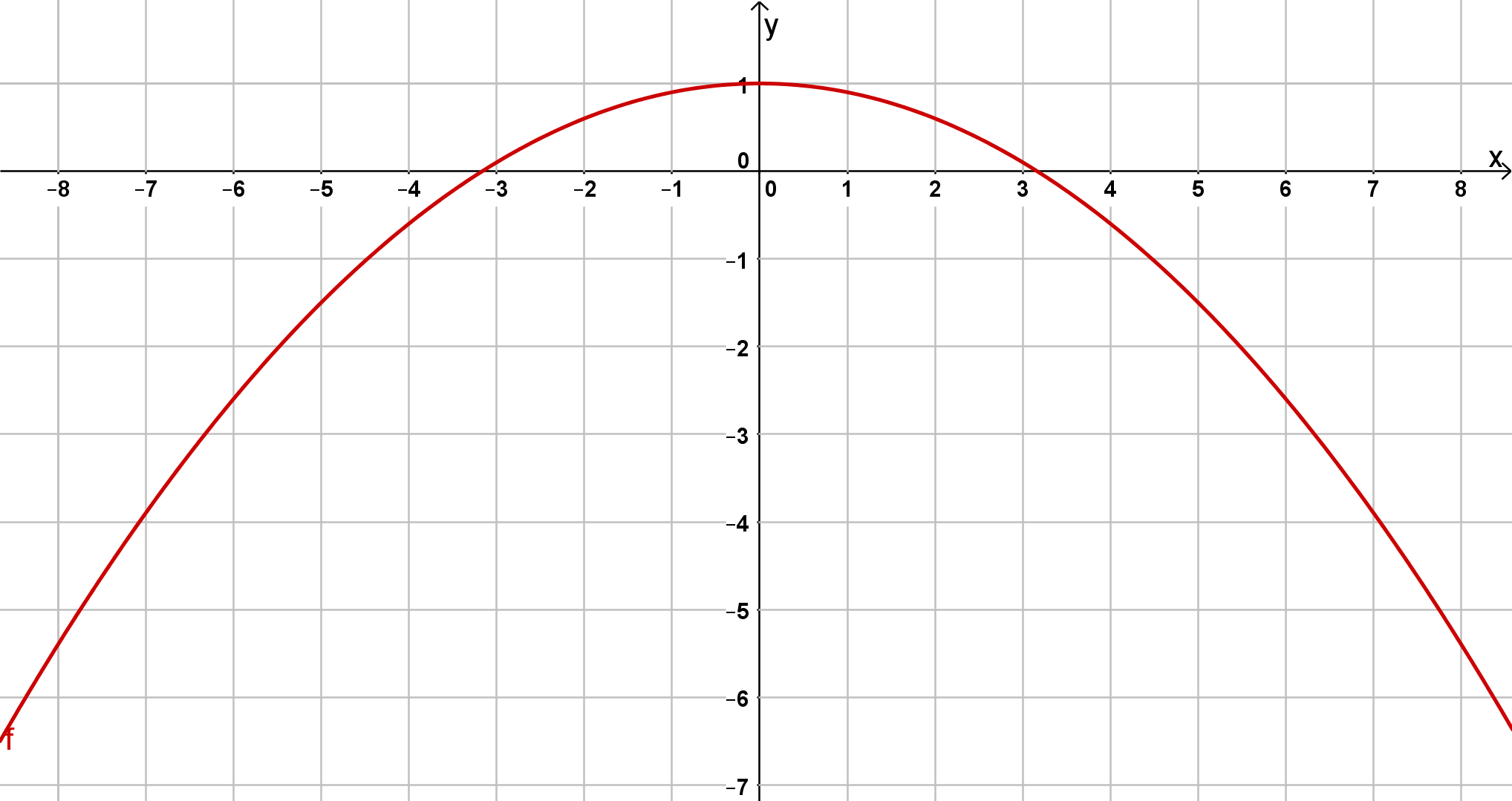
Bestimme jeweils die Scheitelform der unten abgebildeten Parabeln.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterme aufstellen
Funktionsterme angeben
Mittels der Graphen kannst du die jeweiligen Funktionsterme aufstellen.
Lese dafür zunächst die Scheitelpunkte der drei Funktionen aus dem Koordinatensystem ab.
Gib mithilfe der Scheitelpunkte die allgemeine Scheitelform der jeweiligen Funktion an.
Setzte nun einen weiteren Punkt ein um zu berechnen. Hier wurde der Punkt gewählt.
Löse nun nach auf.
Löse nun den Doppelbruch, indem du mit dem Kehrbruch multiplizierst.
Setze nun einen weiteren Punkt ein um zu berechnen. Hier wurde der Punkt verwendet.
Löse nun nach auf.
Setzte nun einen weiteren Punkt ein um zu berechnen. Hier wurde der Punkt gewählt.
Löse nun nach auf.
- 2
Bestimme die Funktionsgleichungen der quadratischen Funktionen mit den gegebenen Informationen.
Der Graph der Funktion verläuft durch die Punkte A(1|1), B(3|4), C(5|-1)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktion aufstellen
Aufstellen einer quadratischen Funktion
Mit ausreichend gegebenen Eigenschaften lassen sich quadratische Funktionen aufstellen.
Setze A, B und C in die allgemeine Gleichung für quadratische Funktionen ein.
Wende das Additionsverfahren an.
:
:
:
Setze in ein.
Setze und in ein.
Hast du eine Frage oder Feedback?
Die Funktion besitzt eine doppelte Nullstelle bei x=3 und geht durch den Punkt P(2|0,3).
Aufstellen einer quadratischen Funktion
Mit ausreichend gegebenen Eigenschaften lassen sich quadratische Funktionen aufstellen.
Da die gesuchte Funktion quadratisch ist, handelt es sich bei der doppelten Nullstelle bei um den Scheitel der Parabel. Damit ist von der Form . Der Parameter lässt sich nun durch Einsetzen des Punktes bestimmen:
Hast du eine Frage oder Feedback?
Die nach unten geöffnete Normalparabel hat den Scheitelpunkt S(2|6).
Aufstellen einer quadratischen Funktion
Mit ausreichend gegebenen Eigenschaften lassen sich quadratische Funktionen aufstellen.
Die Normalparabel ist um zwei Einheiten nach rechts und um sechs Einheiten nach oben verschoben. Zudem ist sie nach unten geöffnet. Damit gilt:
Hast du eine Frage oder Feedback?
Die Funktion hat den Scheitelpunkt S(0|-3) und geht durch den Punkt P(1,5|2).
Aufstellen einer quadratischen Funktion
Mit ausreichend gegebenen Eigenschaften lassen sich quadratische Funktionen aufstellen.
Bestimme und durch den Scheitel .
Setze P in die Funktion ein.
Quadriere
Setze in die Funktion ein.
Hast du eine Frage oder Feedback?
Die Funktion geht durch die Punkte A(2|4), B(3|5), C(-1|13).
Aufstellen einer quadratischen Funktion
Mit ausreichend gegebenen Eigenschaften lassen sich quadratische Funktionen aufstellen.
Hier solltest du wissen, wie du eine Parabel durch drei gegebene Punkte legst. Außerdem brauchst du das Einsetzungsverfahren oder das Additionsverfahren zum Lösen von linearen Gleichungssystemen.
Setze die gegebenen Punktepaare in die Funktionsgleichung
Als erstes solltest du die Potenzen ausrechnen.
Löse das Gleichungssystem. Hier wird die Lösung mittels Einsetzungsverfahren verwendet.
Löse als erstes zum Beispiel Gleichung nach auf.
Setze dieses Ergebnis in die beiden anderen Gleichungen ein.
Vereinfache die beiden Gleichungen.
Löse beispielsweise Gleichung nach auf.
Setze in Gleichung ein und vereinfache.
Setze das Ergebnis für in Gleichung ein, also die Gleichung für ein.
Setze dein Ergebnis für und in die Gleichung für (I') ein.
Deine Ergebnisse sind:
Setze in die allgemeine Funktionsgleichung ein und erhalte die Lösung.
Hast du eine Frage oder Feedback?
- 3
Gib zu den jeweiligen Scheiteln von verschobenen Normalparabeln den Funktionsterm an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen
Bei der Verschiebung der Normalparabel verändert sich der Faktor a nicht. Es verändert sich nur der Scheitelpunkt. Eingesetzt in die Scheitelform ergibt sich:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen
Bei der Verschiebung der Normalparabel verändert sich der Faktor a nicht. Es verändert sich nur der Scheitelpunkt. Eingesetzt in die Scheitelform ergibt sich:
Hast du eine Frage oder Feedback?
- 4
Auf dem Graph der Funktion liegen die folgenden Punkte. Gib für jeden Punkt den Funktionsterm an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen
Setze in die Funktionsgleichung ein:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen
Setze in die Funktionsgleichung an:
Hast du eine Frage oder Feedback?
- 5
Wie lautet die Gleichung einer nach unten geöffneten Normalparabel mit Scheitel ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform
Man kann den Faktor a schon an der Angabe ablesen: eine nach unten geöffnete Normalparabel hat den Faktor -1. In die Scheitelform eingesetzt ergibt sich also :
- 6
Bestimme den Öffnungsfaktor und den Funktionsterm der folgenden Parabeln!
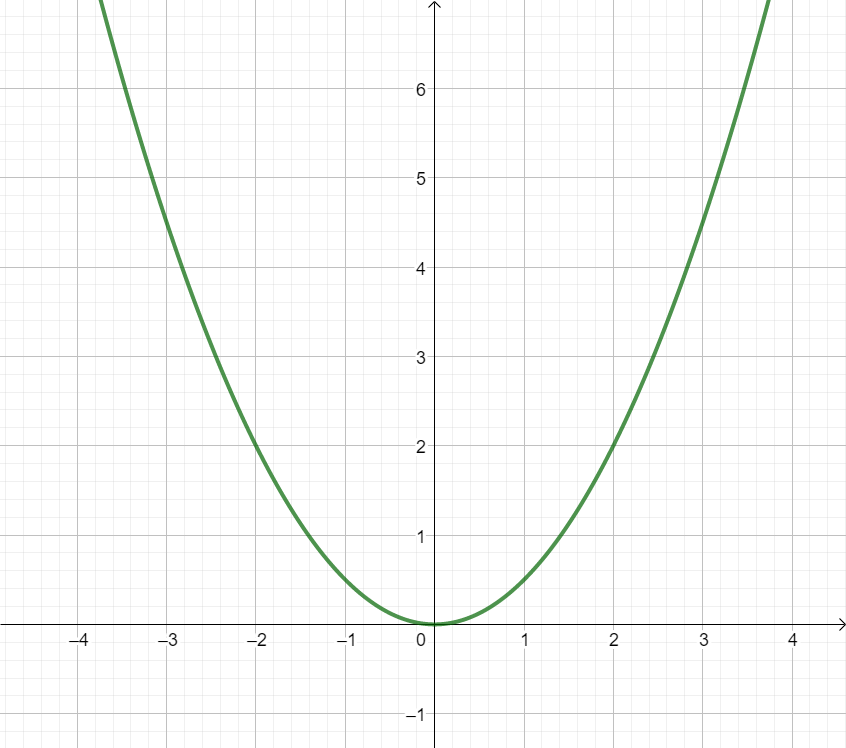
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen für Parabeln
Hier berechnen wir den Funktionsterm, indem wir den Öffnungsfaktor bestimmen und mithilfe eines weiteren Punktes den Funktionsterm ausrechnen.
Suche dir nun einen Punkt, den du gut vom Funktionsgraphen ablesen kannst und der nicht der Scheitelpunkt ist.
Es bietet sich der Punkt an, weil da die Parabel genau eine Kästchen-Ecke trifft.
Setze die Koordinaten des Punktes in die allgemeine Form für die Parabel mit dem Scheitelpunkt ein.
Löse diese Gleichung nach auf!
Der Öffnungsfaktor hat also den Wert .
Aufstellen der Funktionsgleichung
Setze nun den Wert für den Öffnungsfaktor in die allgemeine Funktionsgleichung ein.
Die Funktionsgleichung der Parabel lautet .
Hast du eine Frage oder Feedback?
Hier gibt es verschiedene Lösungsansatze: Du kannst z.B: 3 Punkte ablesen und daraus die Funktion bestimmen oder den Öffnungsfaktor der Parabel bestimmen und dann mit einem weiteren Punkt die Funktion ausrechnen.
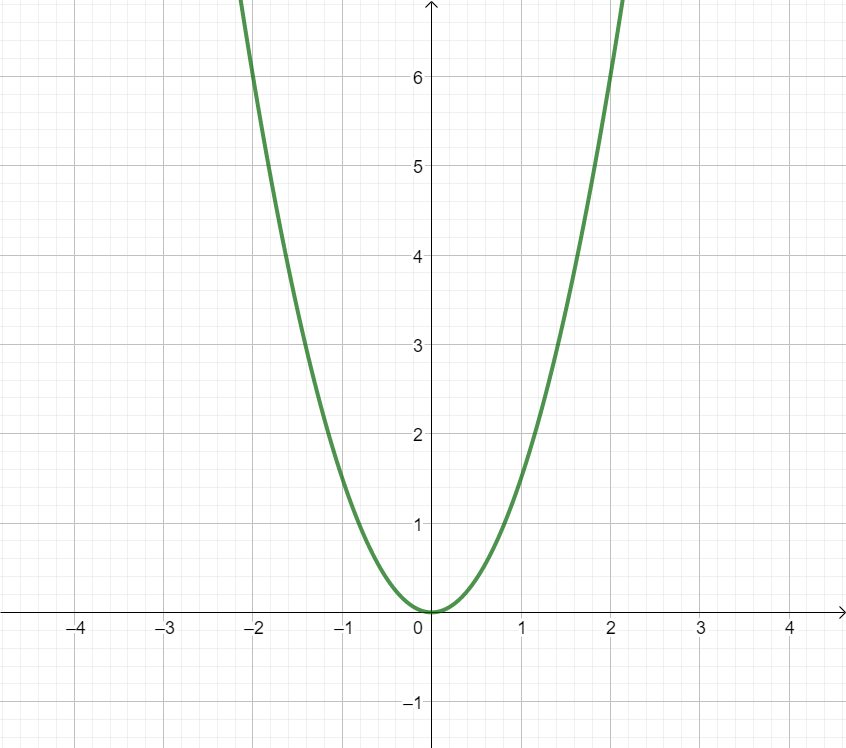
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen für Parabeln
Hier berechnen wir den Funktionsterm, indem wir den Öffnungsfaktor bestimmen und mithilfe eines weiteren Punktes den Funktionsterm ausrechnen.
Suche dir nun einen Punkt, den du gut vom Funktionsgraphen ablesen kannst und der nicht der Scheitelpunkt ist.
Es bietet sich der Punkt an, da da die Parabel genau die Kästchen trifft.
Setze die Koordinaten des Punktes in die allgemeine Form für die Parabel mit dem Scheitelpunkt ein.
Löse diese Gleichung nach auf!
Der Öffnungsfaktor hat also den Wert .
Aufstellen der Funktionsgleichung
Setze nun den Wert für den Öffnungsfaktor in die allgemeine Funktionsgleichung ein.
Damit erhältst du .
Die Funktionsgleichung der Parabel lautet also .
Hast du eine Frage oder Feedback?
Hier gibt es verschiedene Lösungsansatze: Du kannst z.B: 3 Punkte ablesen und daraus die Funktion bestimmen oder den Öffnungsfaktor der Parabel bestimmen und dann mit einem weiteren Punkt die Funktion ausrechnen.
Bestimme den Funktionsterm einer Parabel mit dem Scheitelpunkt , die durch den Punkt geht.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen für Parabeln
Hier berechnen wir den Funktionsterm, indem wir den Öffnungsfaktor bestimmen und mithilfe eines weiteren Punktes den Funktionsterm ausrechnen.
Um den Öffnungsfaktor der Parabel zu bestimmen benötigst du einen Punkt, der nicht der Scheitelpunkt ist. In der Angabe ist schon der Punkt gegeben.
Setze die Koordinaten des Punktes in die allgemeine Form für die Parabel mit dem Scheitelpunkt ein.
Löse diese Gleichung nach auf!
Der Öffnungsfaktor hat also den Wert .
Aufstellen der Funktionsgleichung
Setze nun den Wert für den Öffnungsfaktor in die allgemeine Funktionsgleichung ein.
Damit erhältst du .
Die Funktionsgleichung der Parabel lautet also .
Hast du eine Frage oder Feedback?
Hier gibt es verschiedene Lösungsansatze: Du kannst z.B: 3 Punkte ablesen und daraus die Funktion bestimmen oder den Öffnungsfaktor der Parabel bestimmen und dann mit einem weiteren Punkt die Funktion ausrechnen.
- 7
Zeichne die Graphen der folgenden Funktionen:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel
Überlege dir, was macht das Minus vor dem x und was macht die 3 da. Das Minus öffnet die Parabel nach unten und die 3 macht die Parabel schmaler. Wenn du jetzt noch zwei x-Werte einsetzt kannst du die Funktion gut zeichnen.
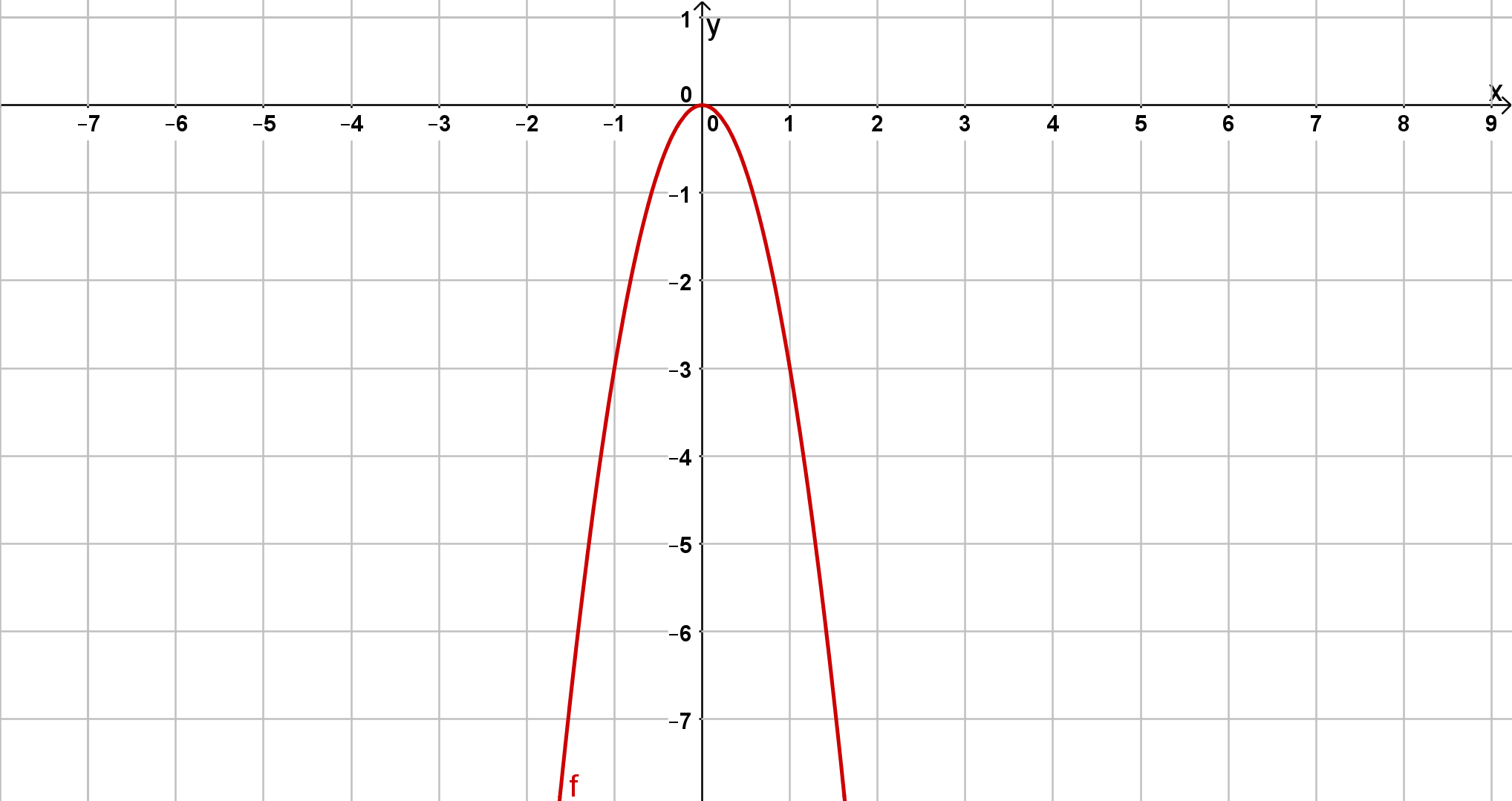
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel
Der Faktor ist kleiner als 1 und macht die Parabel damit breiter.
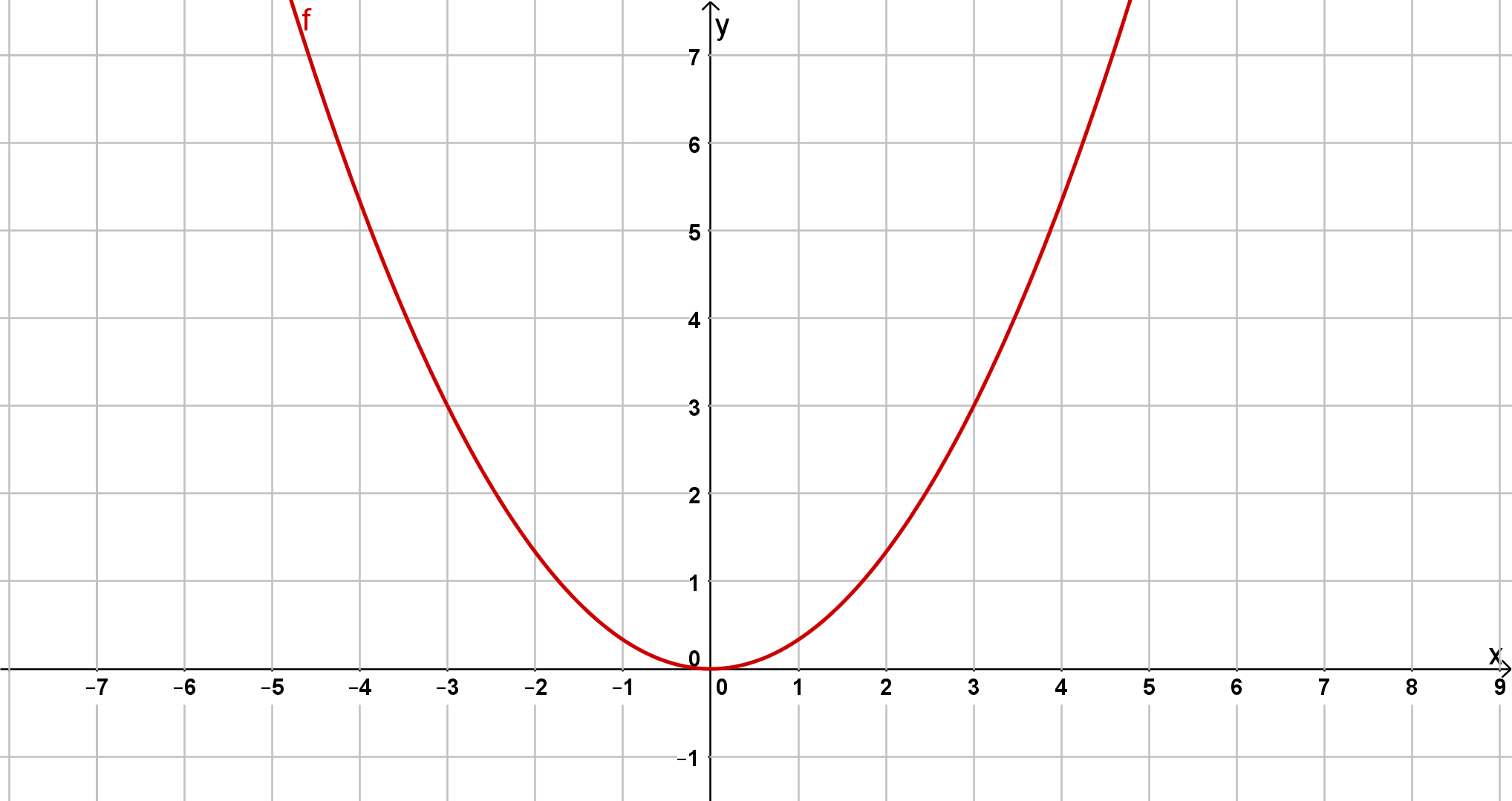
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel
Überlege dir, was die 2 für Auswirkungen auf die Funktion hat. Richtig, in diesem Fall steht das in für die Verschiebung entlang der y-Achse, hier in die negative Richtung wegen dem Minus. Ansonsten ist die Normalparabel.
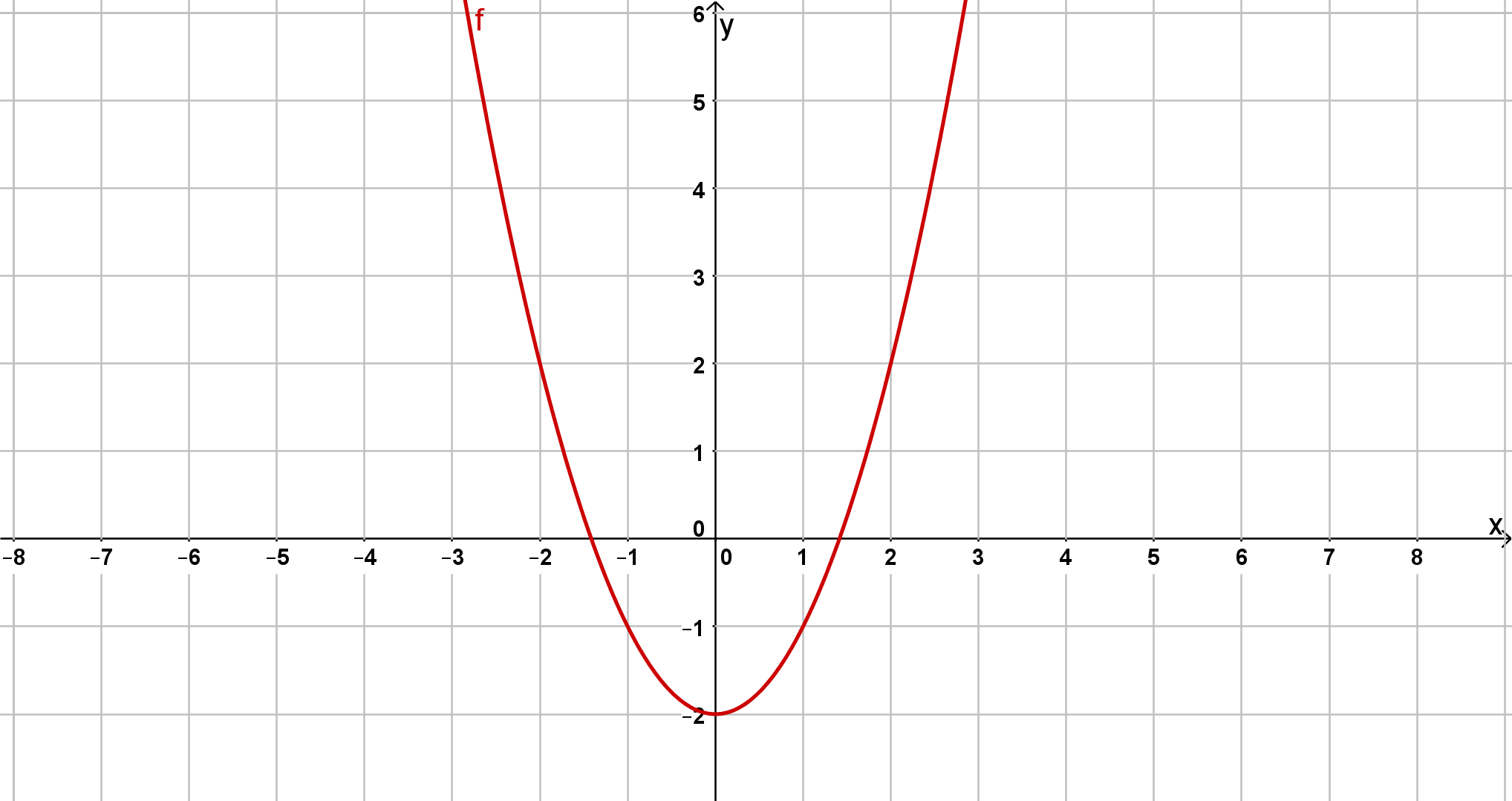
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel
Hier steht nur vor dem noch der Faktor . Dieser öffnet die Parabel weiter.
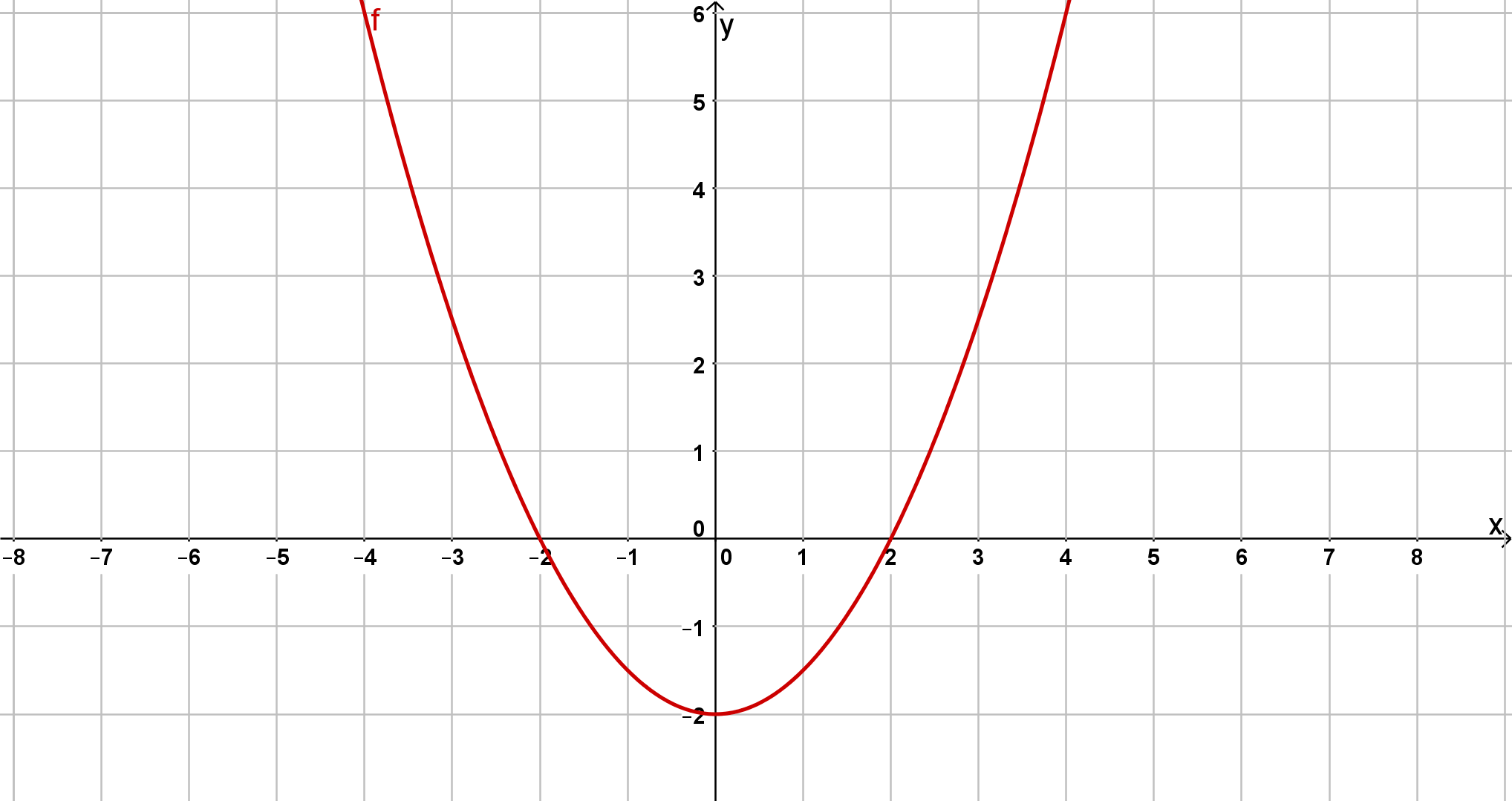
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel
Überlege dir, was das Minus vor dem macht. Außerdem haben wir eine Verschiebung um plus in die y-Richtung.
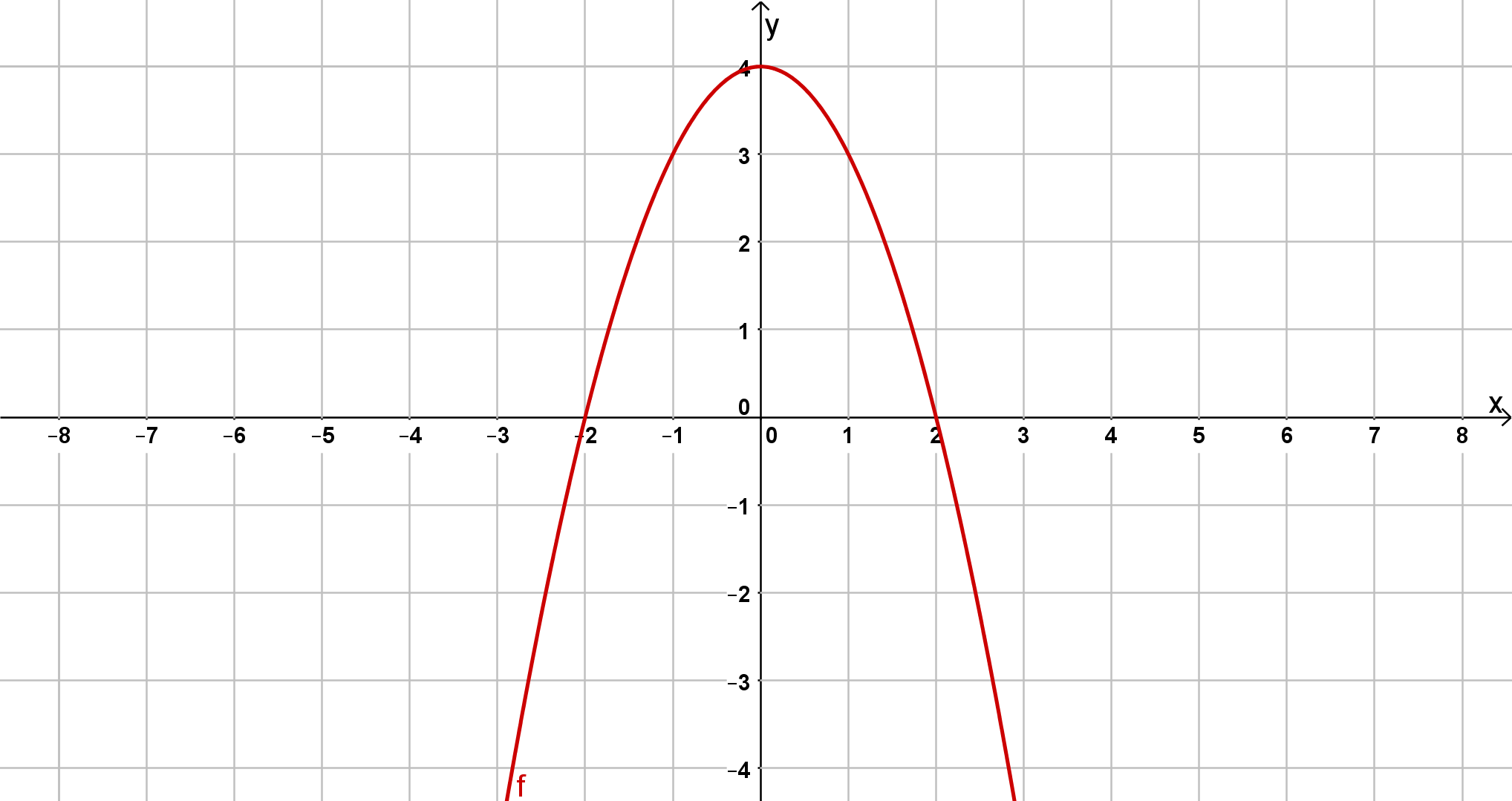
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel
Überlege dir, was die für Auswirkungen auf die Funktion hat.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?