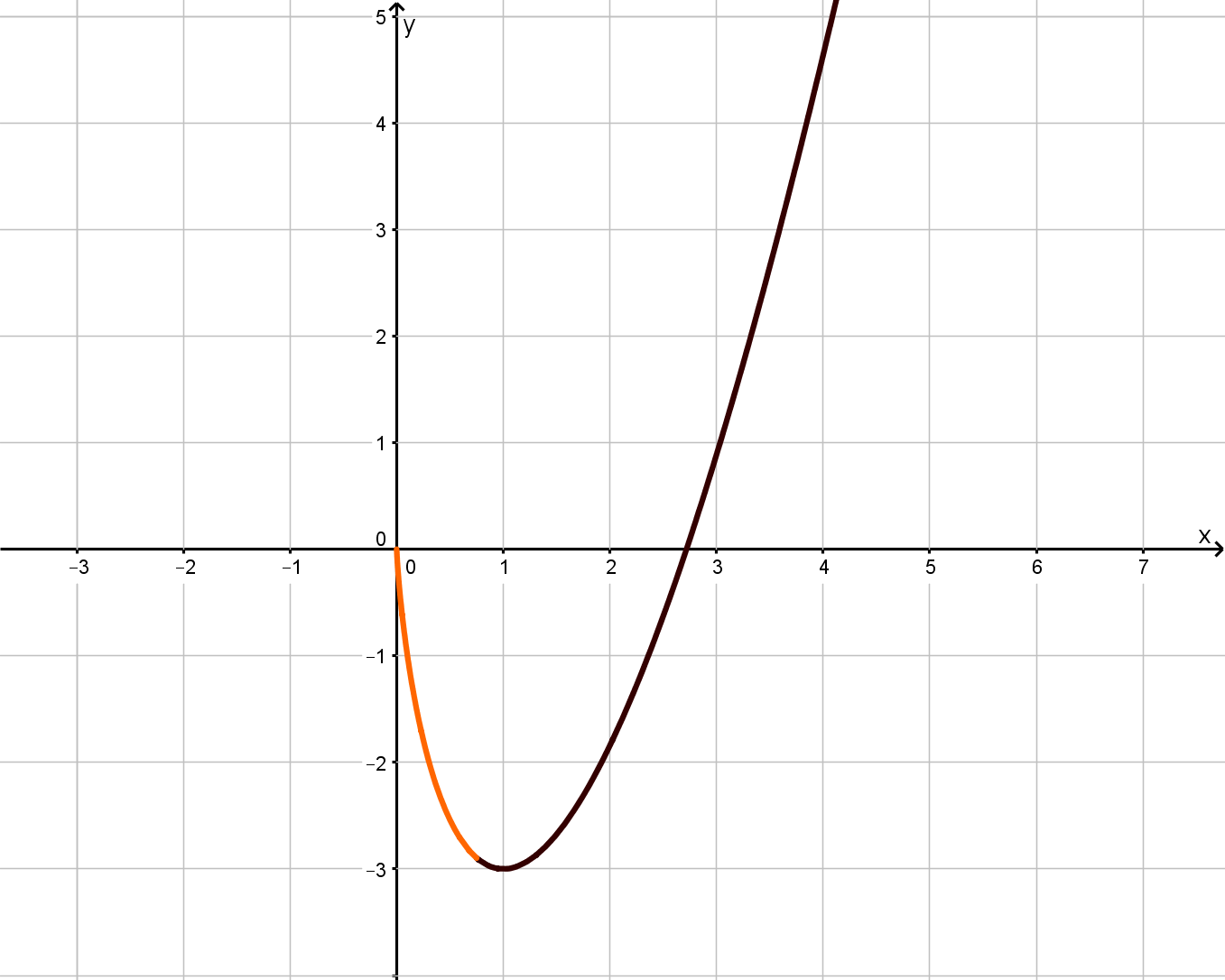
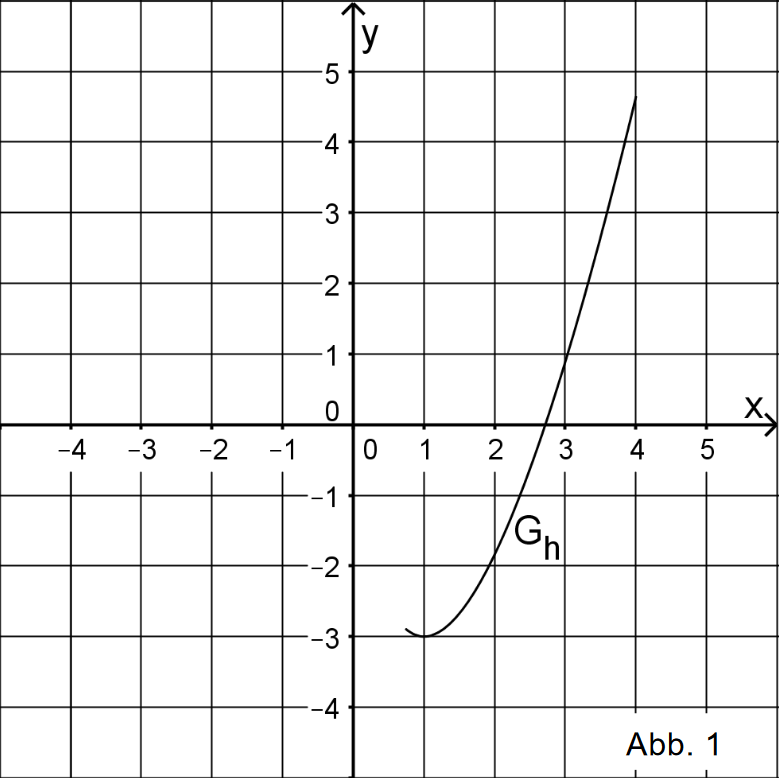
Gegeben ist die in definierte Funktion . Abbildung 1 zeigt den Graphen von im Bereich .
Bestimmen Sie die Gleichung der Tangente an im Punkt und berechnen Sie die Größe des Winkels, unter dem diese Tangente die -Achse schneidet. (4 BE)
(zur Kontrolle: )
Untersuchen Sie das Monotonieverhalten von . Geben Sie den Grenzwert von für an und begründen Sie, dass die Wertemenge von ist. (4 BE)
Geben Sie für die Funktion und deren Ableitungsfunktion jeweils das Verhalten für an und zeichnen Sie im Bereich in Abbildung 1 ein. (3 BE)
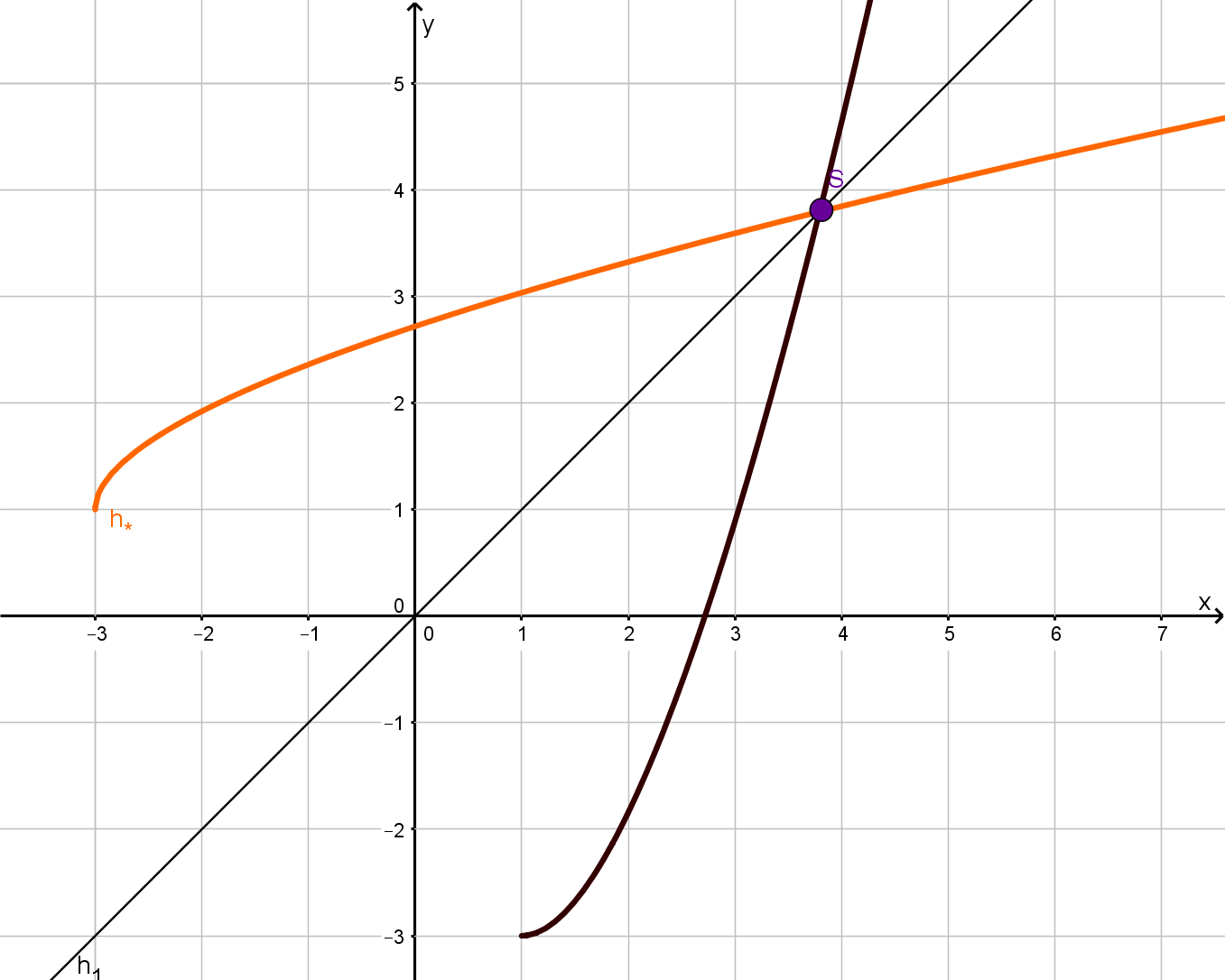
Die Funktion mit Definitionsmenge unterscheidet sich von der Funktion nur hinsichtlich der Definitionsmenge. Im Gegensatz zu ist die Funktion umkehrbar.
Geben Sie die Definitionsmenge und die Wertemenge der Umkehrfunktion von an. Berechnen Sie die Koordinaten des Schnittpunkts des Graphen von und der Geraden mit der Gleichung . (4 BE)
(Teilergebnis: -Koordinate des Schnittpunkts: )
Zeichnen Sie den Graphen der Umkehrfunktion von unter Verwendung der bisherigen Ergebnisse, insbesondere der Lage von Punkt , in Abbildung 1 ein. (3 BE)
Schraffieren Sie in Abbildung 1 ein Flächenstück, dessen Inhalt dem Wert des Integrals entspricht, wobei die -Koordinate von Punkt ist. Der Graph von , der Graph der Umkehrfunktion von sowie die beiden Koordinatenachsen schließen im ersten Quadranten ein Flächenstück mit Inhalt ein. Geben Sie unter Verwendung von einen Term zur Berechnung von an. (4 BE)