In der Lungenfunktionsdiagnostik spielt der Begriff der Atemstromstärke eine wichtige Rolle. Im Folgenden wird die Atemstromstärke als die momentane Änderungsrate des Luftvolumens in der Lunge betrachtet, d.h. insbesondere, dass der Wert der Atemstromstärke beim Einatmen positiv ist. Für eine ruhende Testperson mit normalem Atemrhythmus wird die Atemstromstärke in Abhängigkeit von der Zeit modellhaft durch die Funktion mit Definitionsmenge beschrieben.
Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Sekunden und die Atemstromstärke in Litern pro Sekunde. Abbildung 5 zeigt den durch die Funktion beschriebenen zeitlichen Verlauf der Atemstromstärke.
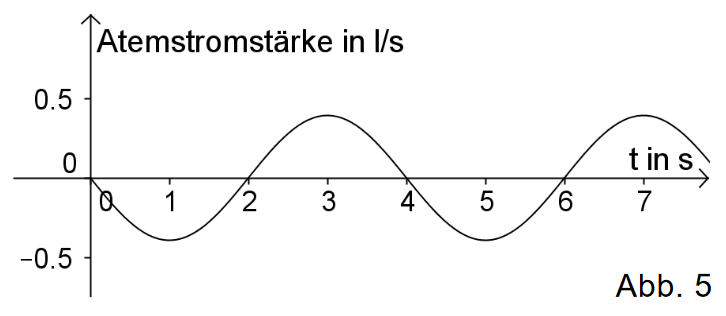
Berechnen Sie und interpretieren Sie das Vorzeichen dieses Werts im Sachzusammenhang. (2 BE)
Beim Atmen ändert sich das Luftvolumen in der Lunge. Geben Sie auf der Grundlage des Modells einen Zeitpunkt an, zu dem das Luftvolumen in der Lunge der Testperson minimal ist, und machen Sie Ihre Antwort mithilfe von Abbildung 5 plausibel. (2 BE)
Berechnen Sie und deuten Sie den Wert des Integrals im Sachzusammenhang. (4 BE)
(Teilergebnis: Wert des Integrals: 0,5)
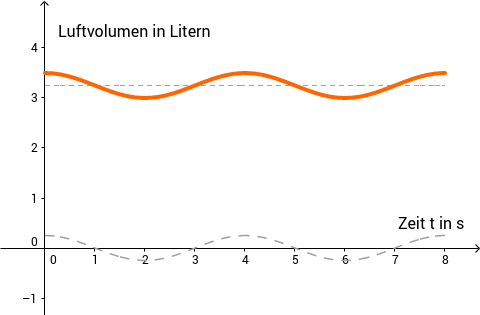
Zu Beginn eines Ausatemvorgangs befinden sich Luft in der Lunge der Testperson. Skizzieren Sie auf der Grundlage des Modells unter Berücksichtigung des Ergebnisses aus Aufgabe 3c in einem Koordinatensystem für den Graphen einer Funktion, die den zeitlichen Verlauf des Luftvolumens in der Lunge der Testperson beschreibt. (3 BE)
Die Testperson benötigt für einen vollständigen Atemzyklus 4 Sekunden. Die Anzahl der Atemzyklen pro Minute wird als Atemfrequenz bezeichnet.
Geben Sie zunächst die Atemfrequenz der Testperson an. Die Atemstromstärke eines jüngeren Menschen, dessen Atemfrequenz um höher ist als die der bisher betrachteten Testperson, soll durch eine Sinusfunktion der Form mit und beschrieben werden. Ermitteln Sie den Wert von . (4 BE)