Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Gruppe A

Die Aufgaben findest du hier zum Ausdrucken als PDF

  1. 1

    Lösen Sie folgende Aufgaben.

    1. Geben Sie für x∈Rx\in\mathbb{R} \ {0} die Lösung der Gleichung 2x=3\dfrac{2}{x}=3 an.

    2. Bestimmen Sie für x∈Rx\in\mathbb{R} die Lösungen der Gleichung 2x2−5x−3=02x^2-5x-3=0.

  2. 2

    Die in R\mathbb{R} definierte Funktion f:x→(x+3)2−4 f:x\rightarrow (x+3)^2-4 hat genau zwei Nullstellen. Die Abbildung zeigt den Graphen GfG_f von f.

    Bild

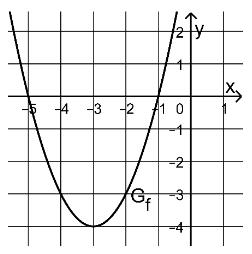
    1. GfG_f schneidet die y-Achse im Punkt P. Berechnen Sie die y-Koordinate von P.

    2. Betrachtet wird nun allgemein für jeden Wert b∈Rb\in\mathbb{R} die in R\mathbb{R} definierte Funktion

      fb:x→(x+3)2+bf_b: x\rightarrow(x+3)^2+b

      Geben Sie an, für welche Werte von b die Funktion fbf_b keine Nullstelle besitzt

    3. Betrachtet wird ferner für jeden Wert a∈Ra\in\mathbb{R} die in R\mathbb{R} definierte Funktion

      fa:x→(x+a)2−4f_a: x\rightarrow(x+a)^2-4

      Begründen Sie, dass die Funktion faf_a für jeden Wert von a zwei Nullstellen besitzt.

  3. 3

    Am 3. Oktober 1990 wurde die deutsche Wiedervereinigung vollzogen.

    1. Im abgebildeten Kreisdiagramm ist der Anteil p der Einwohner Gesamtdeutschlands dargestellt, die im Jahr 1990 im Gebiet der ehemaligen DDR lebten. Der Mittelpunktswinkel des zugehörigen grau gefärbten Sektors beträgt 72°.72°.

      Bild

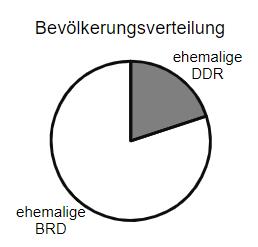
      Berechnen Sie den Anteil p in Prozent.

    2. Gemäß einer repräsentativen Umfrage aus dem Jahr 2018 unter jungen Deutschen waren 69% der jungen Westdeutschen, aber nur 56% der jungen Ostdeutschen der Meinung, dass es nach wie vor kulturelle Unterschiede zwischen Ost-und Westdeutschen gibt. Basierend auf diesen Daten soll der Anteil aller jungen Deutschen berechnet werden, die 2018 der Meinung waren, dass es nach wie vor kulturelle Unterschiede zwischen Ost-und Westdeutschen gibt.

      Beurteilen Sie, ob dafür der Ansatz (69%+56%):2 geeignet ist.

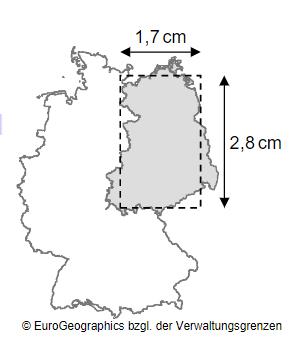
    3. Die nebenstehende Karte zeigt Deutschland im Maßstab 1: 15 000 000.

      Durch eine Abschätzung mithilfe des eingezeichneten Rechtecks soll ein Näherungswert für den Inhalt der Fläche Ostdeutschlands (in der Karte grau dargestellt) ermittelt werden.

      Geben Sie mithilfe der angegebenen Seitenlängen einen Ansatz zur Berechnung des Flächeninhalts Ostdeutschlands in km2km^2 an.

      Bild
  4. 4

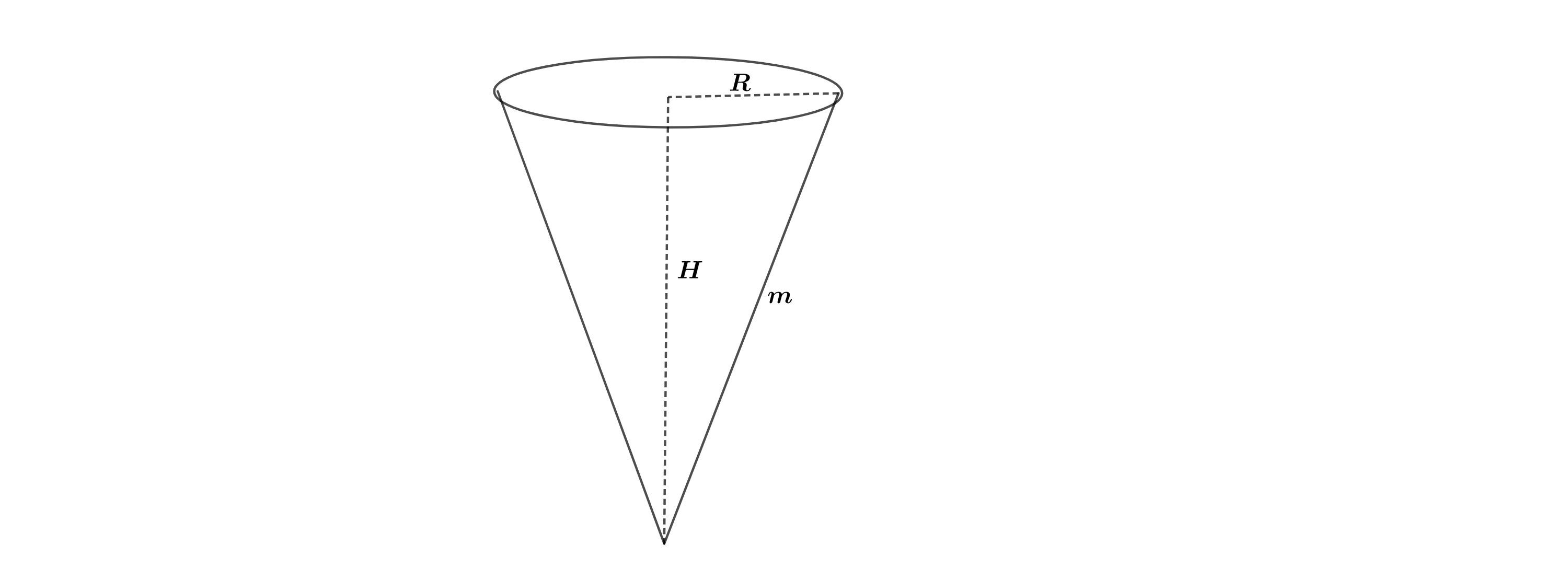
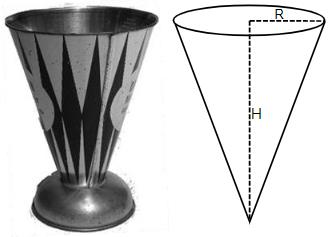
    Mit dem abgebildeten Messbecher kann das Volumen von Flüssigkeiten abgemessen werden. Er kann modellhaft als Kegel mit Gesamthöhe H und Grundkreisradius R betrachtet werden (vgl. Skizze).

    Bild

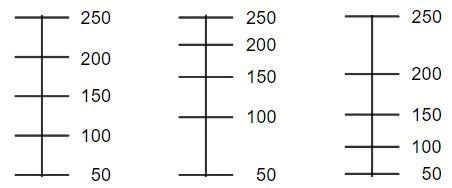
    1. Der Messbecher ist innen mit einer Skala beschriftet, sodass das Volumen der eingefüllten Flüssigkeit in ml abgelesen werden kann. Eine der drei nachfolgenden Skalen ist grundsätzlich dafür geeignet. Welche Skala ist das?

      Bild

    2. Der Messbecher ist nun 10cm hoch mit Wasser gefüllt; der Radius des Wasserspiegels beträgt 4cm.

      Berechnen Sie, wie groß das Volumen des Wassers im Messbecher in etwa ist. Verwenden Sie dazu den Näherungswert π≈3\pi \approx3.

    3. Die Mantelfläche des Messkegels mit Grundkreisradius R und Gesamthöhe H wird aus einem Stück Blech gefertigt, das die Form eines Kreissektors hat. Dieser Sektor hat die Bogenlänge b und den Radius m (vgl. Abbildung)

      Bild

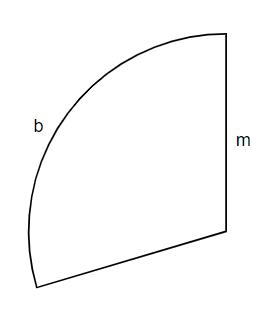
      Erklären Sie anschaulich, warum b=2π⋅Rb=2\pi\cdot R gilt.

    4. Geben Sie eine Gleichung an, die den Zusammenhang von m, R und H beschreibt.

  5. 5

    Lösen Sie folgende Aufgaben.

    1. Ergänzen Sie folgenden Text fachsprachlich korrekt

      Bild
    2. Bild

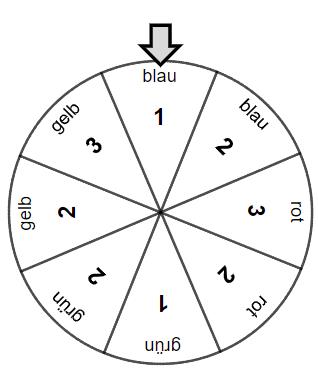
      Ein Glücksrad hat acht gleich große Sektoren, die gefärbt und mit Zahlen beschriftet sind (vgl. Abbildung). Das Glücksrad wird zweimal gedreht. Nach der ersten Drehung wird die dabei erzielte Zahl, nach der zweiten Drehung die dabei erzielte Farbe notiert. Betrachtet wird das Ereignis EE: „Das Rad zeigt zuerst eine ungerade Zahl und dann rot.“Bestimmen Sie die Wahrscheinlichkeit des Gegenereignisses E‾\overline E von EE.

  6. 6

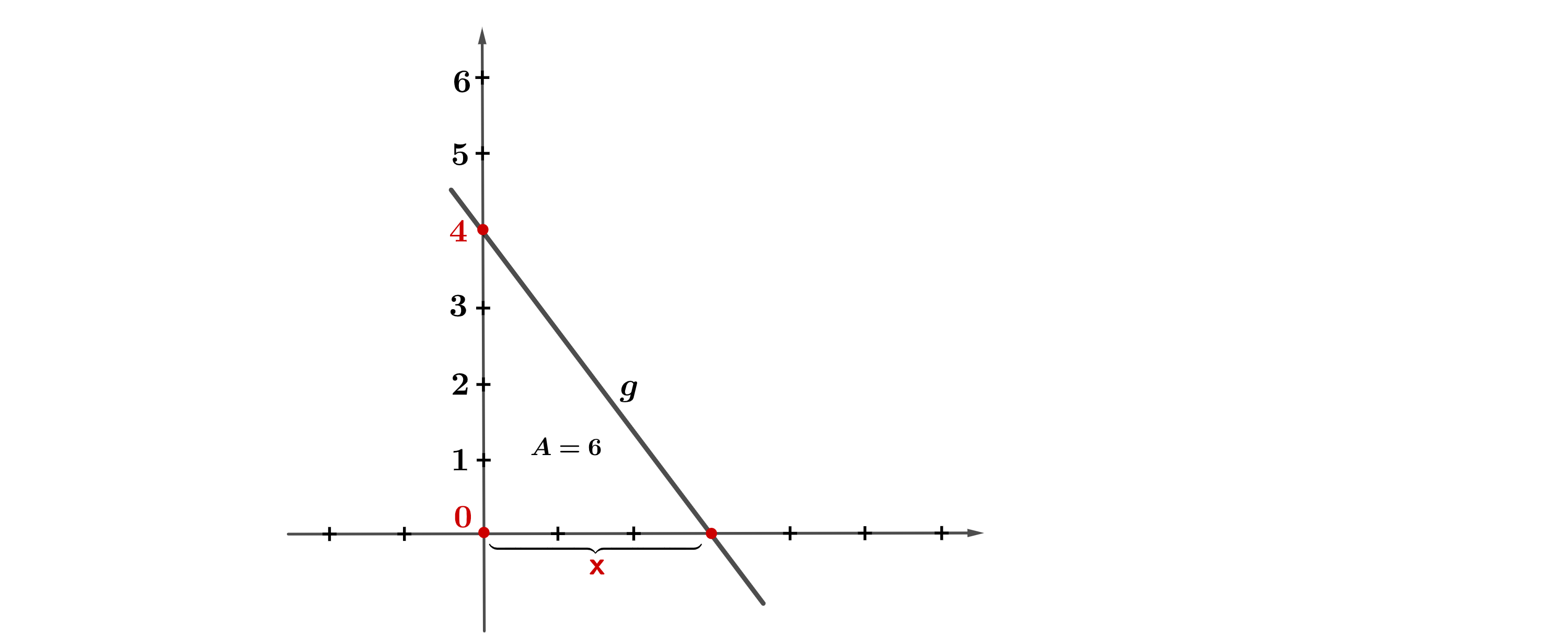
    Für jeden Wert m∈Rm\in\mathbb{R} wird die Gerade mit der Gleichung y=m⋅x+4y=m\cdot x+4 betrachtet.

    1. Zeichnen Sie in ein Koordinatensystem, (siehe Abb.) die Gerade zu m=−2m=-2 ein.

      Bild

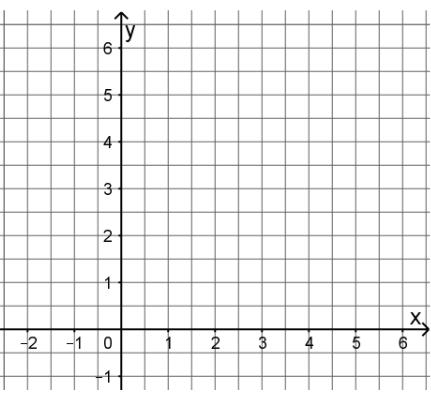
    2. Ermitteln Sie den Wert von mm so, dass das Dreieck, das die zugehörige Gerade im ersten Quadranten mit den beiden Koordinatenachsen einschließt, den Flächeninhalt 66 hat.


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?