Gruppe A

Die Aufgaben findest du hier zum Ausdrucken als PDF.

1
Bestimmen Sie für $x\in\mathbb{R}$ die Lösungen der Gleichung $2x^2+x-10=0$

$ax^2+bx+c=0$
$x_{1{,}2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$
$2x^2+x-10=0$
$\Rightarrow$ $a=2$ ; $b=1$ ; $c=-10$
$x_{1{,}2}=\dfrac{-1\pm\sqrt{(1)^2-4\cdot 2\cdot (-10)}}{2\cdot 2}$
$x_{1{,}2}=\dfrac{-1\pm\sqrt{1+80}}{4}$
$x_{1{,}2}=\dfrac{-1\pm9}{4}$
$x_1=2$ ; $x_2=-2{,}5$
2
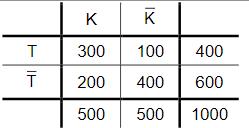
Bei einer Untersuchung von Bäumen werden folgende Ereignisse betrachtet:
T: „Der untersuchte Baum weist einen Schaden durch Trockenheit auf.“
K: „Der untersuchte Baum weist einen Schaden durch Käferbefall auf.“
In nebenstehender Vierfeldertafel sind die Untersuchungsergebnisse für einen Waldbereich mit 1000 Bäumen dargestellt.
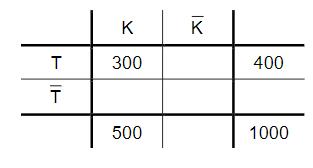
1. Füllen Sie die Vierfeldertafel vollständig aus.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Einer der 1000 Bäume wird nun zufällig ausgewählt.
  Geben Sie die Wahrscheinlichkeit $P(T\cup K)$ in Prozent an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vereinigungsmenge
  $P(T\cup K)=400+(500-300)=600$
  $600$ von $1000$ $\mathop{\widehat{=}}$ $60$ %
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Kreuzen Sie (nur) die Beschreibung an, die zum Ereignis $(T\cap\overline K)\cup (\overline T\cap K)$
  passt.
  „Der Baum weist keinen der beiden Schäden auf.“
  „Der Baum weist genau einen der beiden Schäden auf.“
  „Der Baum weist beide Schäden auf.“
  „Der Baum weist mindestens einen der beiden Schäden auf.“
3
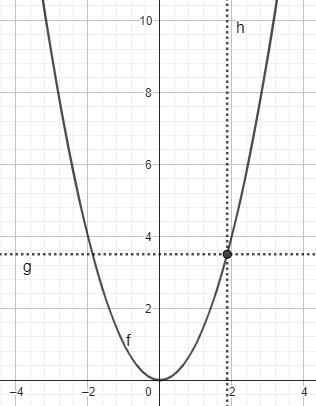
Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion f: $x\rightarrow x^2$
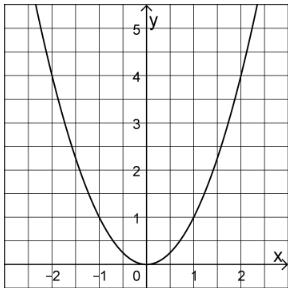
1. Beschreiben Sie allgemein, was man unter der Wertemenge einer Funktion versteht, und geben Sie die Wertemenge von f an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertemenge
  In der Wertemenge befinden sich nur die Werte, die wirklich von der Funktion angenommen werden, also die Menge aller Funktionswerte.
  Wertmenge von f : $\mathbb{R}_0^+$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Ermitteln Sie mithilfe geeigneter Eintragungen in der Abbildung einen Näherungswert für $\sqrt{3{,}5}.$
  
  $\sqrt{3{,}5}\approx1{,}9$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Zeichne eine Parallele zur x-Achse: $y=3{,}5$
  zeichne eine Parallele zur y- Achse durch den Schnittpunk der Geraden $y=3{,}5$ mit der Funkti0n $y=x^2$ .
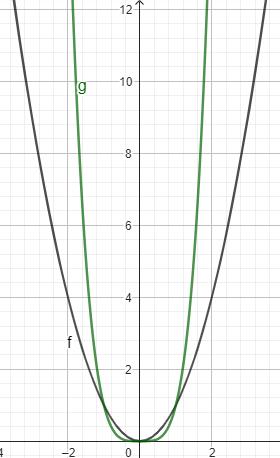
3. Skizzieren Sie den Graphen der in $\mathbb{R}$ definierten Funktion g: $x\rightarrow x^4$ in der Abbildung.
  
  $y=x^4$ wird durch die grün gezeichnete Funktion $g$ dargestellt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Gegeben ist der Term $\dfrac{2x-x^2}{2x-4}.$
1. Begründen Sie, dass der Term nicht für alle reellen Zahlen definiert ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchterme
  Der Bruch $\dfrac{2x-x^2}{2x-4}$ ist nicht definiert für $x=2$ , da dann der Nenner Null wäre.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Kürzen Sie den Term so weit wie möglich.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ausklammern
  $\dfrac{2x-x^2}{2x-4}=\dfrac{x\cdot(2-x)}{-2\cdot(2-x)}=- \dfrac{x}{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5
Bei Feinstaubmessungen verwendet man die Einheit Mikrogramm ( $μg$ ). Es gilt $1μg=10^{-6}g.$
1. In einem Klassenzimmer befinden sich $6000μg$ Feinstaub. Geben Sie diesen Wert ohne Potenzschreibweise in der Einheit Gramm an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
  $1μg=10^{-6}g=\dfrac{1}{10^6}g$
  $6000μg=\dfrac{6000}{1000000}g=0{,}006g$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Die gezackte Linie in der Abbildung stellt für den Zeitraum von Januar 2013 bis Dezember 2020 die Monatsmittelwerte der Feinstaubbelastung in $\dfrac{μg}{m^3}$ am Königsplatz in Augsburg dar.
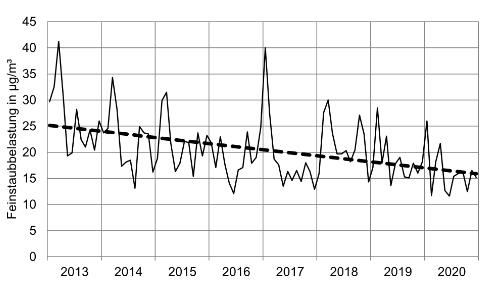
  Im Jahr 2017 betrug der größte Monatsmittelwert $40\dfrac{μg}{m^3}$ . Geben Sie an, um wie viel Prozent der größte Monatsmittelwert im Jahr 2018 niedriger war als im Jahr 2017.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentrechnung mittels Dreisatz
  Größter Monatsmittelwert 2017: $40\dfrac{μg}{m^3}$
  $40\dfrac{μg}{m^3}\mathop{\widehat{=}}$ 100 %
  Größter Monatsmittelwert 2018: $30\dfrac{μg}{m^3}$
  Differenz größter Monatsmittewert 2017 und 2018: $10\dfrac{μg}{m^3}$
  $10\dfrac{μg}{m^3}\mathop{\widehat{=}}100$ % : $4=25$ %
  Der größte Monatsmittelwert im Jahr 2018 war um 25% niedriger als im Jahr 2017.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Die gestrichelte Linie in der Abbildung in b) zeigt die grobe Entwicklung der Feinstaubbelastung ohne kurzfristige Schwankungen. Diese grobe Entwicklung wird modellhaft durch eine lineare Funktion $f$ beschrieben. Dabei ist $x$ die Zahl der Jahre, die seit dem Jahresbeginn 2013 vergangen sind, und $f(x)$ die Feinstaubbelastung in $\dfrac{μg}{m^3}.$
  Der Graph von $f$ ist eine Gerade, die durch die Punkte $(0 | 25)$ und $(6 | 18)$ verläuft. Bestimmen Sie rechnerisch eine Gleichung dieser Gerade.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
  $y=mx+t$
  $P(x_1|y_1)$ = $P(0|25)$ und $Q(x_2|y_2)=Q(6|18)$
  $m=\dfrac{y_2-y_1}{x_2- x_1}$
  $m=\dfrac{18-25}{6- 0}=-\dfrac{7}{6}$
  $y=-\dfrac{7}{6}x+t$
  Setze einen der beiden Punkte in die Geradengleichung ein, z.B. $P(0|25)$ .
  $25=-\dfrac{7}{6}\cdot 0+t$
  $t=25$
  $y=-\dfrac{7}{6}x+25$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Die Funktion $f$ soll für eine Vorhersage der Entwicklung in den nächsten Jahren verwendet werden. Beschreiben Sie, wie man mithilfe der Funktion $f$ ermitteln könnte, wie viele Jahre nach Beginn des Jahres 2013 diese Vorhersage erstmals eine Feinstaubbelastung von weniger als $10\dfrac{μg}{m^3}$ liefert.
  
  $f(x)=-\dfrac{7}{6}x+25$
  Die Lösung der Gleichung $f(x)=10$ liefert die gesuchte Anzahl der Jahre.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6
Lösen Sie die folgenden Aufgaben
1. Geben Sie mithilfe der Abbildung einen Näherungswert für $\sin 53^\circ$ an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus
  $\sin (\alpha )=\dfrac{\text{Gegenkathete}}{\text{Hypotenuse}}$
  Gegenkathede = $0{,}8$
  Hypothenuse = $\sqrt{0{,}6^2+0{,}8^2}=\sqrt{1}=1$
  $\sin (53^\circ)=\dfrac{0{,}8}{1}=0{,}8$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
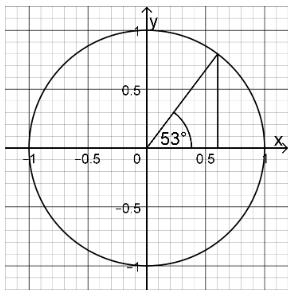
2. Es gilt $\sin 30°=0{,}5$ . Begründen Sie, dass in einem rechtwinkligen Dreieck mit den Kathetenlängen $8cm$ und $15cm$ und der Hypotenusenlänge $17cm$ kein Innenwinkel die Größe $30°$ hat.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus
  $\sin (\alpha )=\dfrac{\text{Gegenkathete}}{\text{Hypotenuse}}$
  $\sin 30°=0{,}5$
  $\dfrac{8}{17}=0{,}47$
  $\dfrac{15}{17}=0{,}88$
  Keiner der beiden Quotienten ergibt $0{,}5.$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7
Ein DIN-A3-Blatt lässt sich durch einen Schnitt in zwei DIN-A4-Blätter zerlegen.
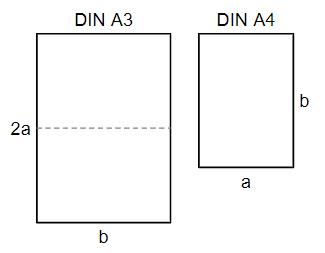
In der Abbildung werden ein DIN-A3 und ein DIN-A4-Blatt durch Rechtecke mit den Seitenlängen 2a und b bzw. b und a veranschaulicht. Die beiden Rechtecke sind zueinander ähnlich, d.h., die Verhältnisse der Längen sich entsprechender Seiten stimmen überein. Begründen Sie, dass $\dfrac{b}{a}=\sqrt{2}$ gilt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ähnlichkeit
Sind zwei ähnliche Figuren $A$ und $B$ gegeben, so stehen alle ihre Seiten im gleichen Verhältnis zueinander. Dieses wird der Ähnlichkeitsfaktor $k$ genannt.
$\Rightarrow$ $\dfrac{2a}{b}=\dfrac{b}{a}$
$2a^2=b^2$
$\sqrt{2}=\dfrac{b}{a}$