Teil 1 Analysis

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgaben zum Ausdrucken als PDF findest du hier

Die Aufgaben in diesem Ordner sollen ohne Hilfsmittel wie Taschenrechner oder Formelsammlung bearbeitet werden.

Gegeben ist die Funktion $g:x\mapsto-\frac 1 4x^4+2x^2$ mit der Definitionsmenge $D_{g} = [- 3; 3]$ . Ihr Graph in einem kartesischen Koordinatensystem wird mit $G_{g}$ bezeichnet.

Untersuchen Sie den Graphen der Funktion $g$ auf Symmetrie zum Koordinatensystem. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
Symmetrieuntersuchung
Da alle Exponenten gerade sind, kann eine Achsensymmetrie zur y-Achse vorliegen.
Eingeschränkte Definitionsmenge
Um final zu entscheiden, ob eine Symmetrie vorliegt, muss auch die Definitionsmenge passen.
Die Definitionsmenge $D_{g} = [- 3; 3]$ ist gleichmäßig um den Ursprung verteilt.
Somit liegt tatsächlich eine Achsensymmetrie zur y-Achse vor.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Du kannst die Symmetrie einer ganzrationalen Funktion untersuchen, indem du die Exponenten betrachtest oder -x in die Funktion einsetzt.
Beachte die eingeschränkte Definitionsmenge!

Ermitteln Sie alle Extremstellen der Funktion $g$ . (4 BE)

Die folgende Abbildung zeigt einen Ausschnitt des Graphen $G_{f}$ einer ganzrationalen Funktion $f$ zweiten Grades mit der Definitionsmenge $D_f=\R$ .

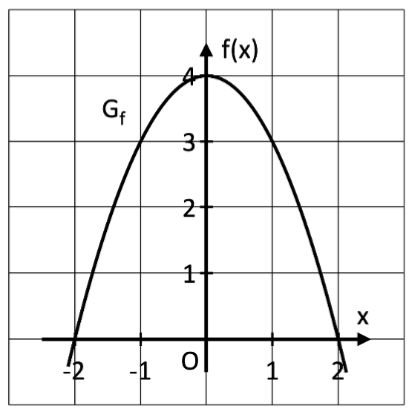
Der Graph der Funktion f und die x-Achse schließen ein endliches Flächenstück ein. Berechnen Sie die Maßzahl des Flächeninhalts dieses Flächenstücks. (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bestimmtes Integral berechnen

Funktionsterm aufstellen

Es gibt verschiedene Wege, den Funktionsterm zu ermitteln. Hier wird die Produktform verwendet:

$f(x)=a(x-x_1)\cdot(x-x_2)$

Die beiden Nullstellen $x_{1} = - 2$ und $x_{2} = 2$ kannst du dem Graphen entnehmen.

$f (x) = a (x - (- 2)) (x - 2) = a (x + 2) (x - 2)$

Um den Öffnungsfaktor a zu bestimmen, setze zum Beispiel den Punkt $P (0 ∣ 4)$ ein:

$\displaystyle f\left(0\right)$	$=$	$\displaystyle 4$
$\displaystyle a\left(0+2\right)\left(0-2\right)$	$=$	$\displaystyle 4$
$\displaystyle a\cdot\left(-4\right)$	$=$	$\displaystyle 4$	$\displaystyle :\left(-4\right)$
$\displaystyle a$	$=$	$\displaystyle -1$

Multipliziere den fertigen Funktionsterm aus, damit du im nächsten Schritt gut integrieren kannst:

$\displaystyle f\left(x\right)$	$=$	$\displaystyle -1\left(x+2\right)\left(x-2\right)$
	$=$	$\displaystyle -1\left(x^2-4\right)$
	$=$	$\displaystyle -x^2+4$

bestimmtes Integral

Bestimme den Flächeninhalt, indem du das bestimmte Integral für $x\in[-2;2]$ berechnest.

$\displaystyle \int_{-2}^2f\left(x\right)dx$	$=$	$\displaystyle \int_{-2}^2\left(-x^2+4\right)dx$
	↓	Bilde eine Stammfunktion
	$=$	$\displaystyle \left[-\frac{1}{3}x^3+4x\right]_{-2}^2$
	↓	Statt den Grenzen $x = - 2$ und $x = 2$ kann man aufgrund der Achsensymmetrie auch das Doppelte vom Integral $\int_0^2f(x) dx$ berechnen
	$=$	$\displaystyle 2\cdot\left[-\frac{1}{3}x^3+4x\right]_0^2$
	↓	Setze die obere Grenze und die untere Grenze ein und subtrahiere
	$=$	$\displaystyle 2\cdot\left(\left(-\frac{1}{3}\cdot2^3+4\cdot2\right)-\left(-\frac{1}{3}\cdot0^3+4\cdot0\right)\right)$
	$=$	$\displaystyle 2\cdot\left(-\frac{8}{3}+8\right)$
	$=$	$\displaystyle 2\cdot\left(\frac{24}{3}-\frac{8}{3}\right)$
	$=$	$\displaystyle 2\cdot\frac{16}{3}$
	$=$	$\displaystyle \frac{32}{3}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

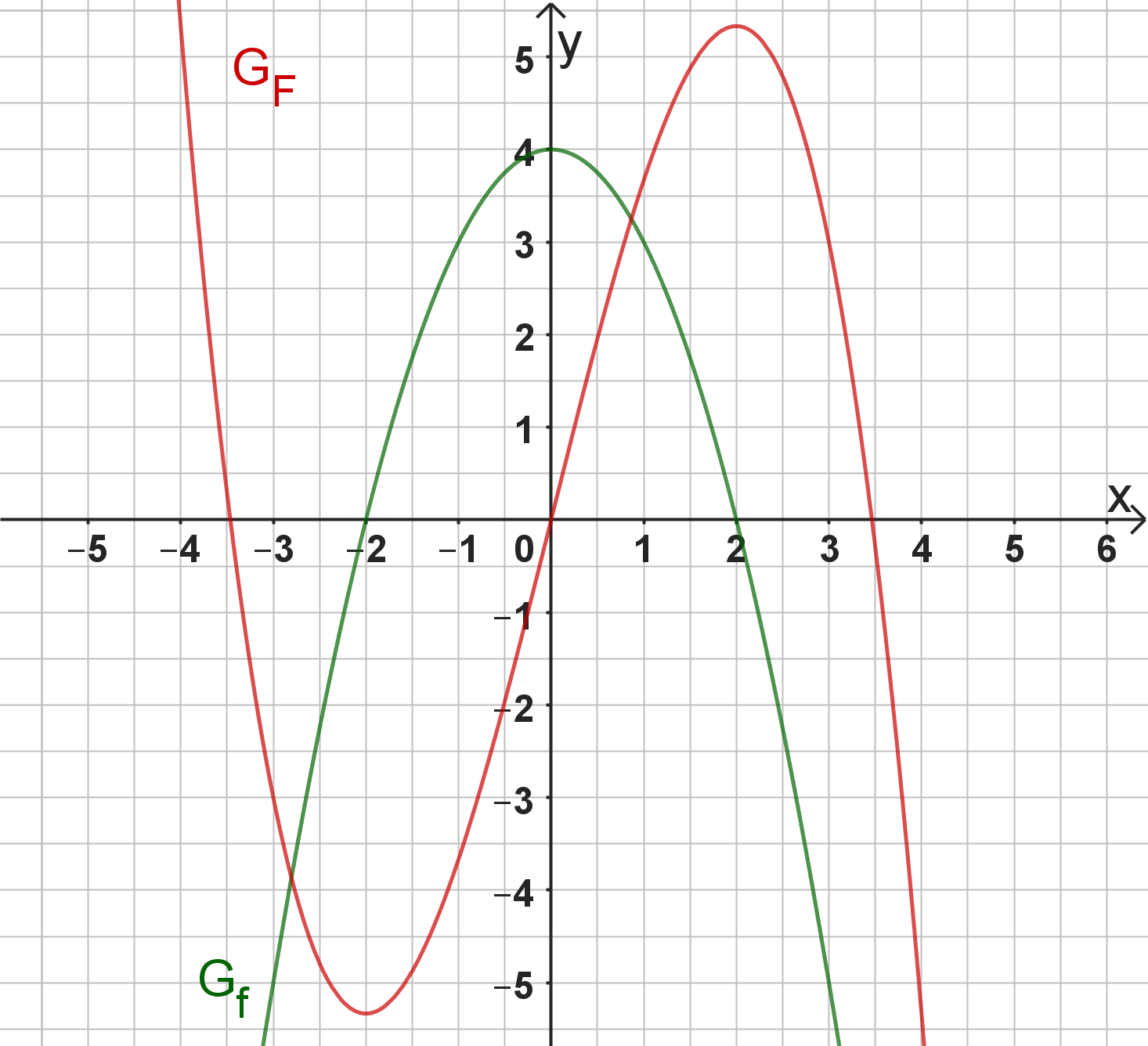
Die Funktion F mit der Definitionsmenge $D_F=\mathbb{R}$ ist eine Stammfunktion von f. Ihr Graph in einem kartesischen Koordinatensystem wird mit $G_{F}$ bezeichnet.
Beschreiben Sie den Globalverlauf des Graphen $G_{F}$ in Worten. Gehen Sie auch auf das Monotonieverhalten, die Lage und die Art der Extremstellen sowie auf die Lage der Wendestellen von $F$ ein. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Monotonieverhalten
Immer, wenn $G_{f}$ unterhalb der x-Achse verläuft, fällt der Graph von $G_{F}$ . Ist er oberhalb der x-Achse, steigt $G_{F}$ :
$G_{F}$ fällt für $x < - 2$ und $x > 2$
$G_{F}$ steigt für $- 2 < x < 2$
Extremstellen
Aus dem Monotonieverhalten kannst du die Extremstellen bestimmen:
Der Graph von $G_{F}$ wechselt bei $x = - 2$ von fallend zu steigend: Dort liegt ein Tiefpunkt
Der Graph $G_{F}$ wechselt bei $x = 2$ von steigend zu fallend: Dort liegt ein Hochpunkt
Globalverlauf von $G_{F}$
Da $G_{f}$ zu Beginn unterhalb der x-Achse verläuft, fällt der Graph von $G_{F}$ für $x\to -\infty$ . Er muss also von links oben kommen und es gilt $lim_{x\to-\infty}F(x)=+\infty$ .
Für $x\to +\infty$ ist der Graph von $f$ erneut unterhalb der x-Achse, das heißt der Graph $G_{F}$ fällt für $x\to+\infty$ : $lim_{x\to+\infty}F(x)=-\infty$ .
Wendestelle
Die Wendestellen liegen bei den Nullstellen (mit Vorzeichenwechsel) der zweiten Ableitung. Dies sind zugleich die Extremstellen der 1. Ableitung.
Somit ist die Wendestelle bei $x = 0$ .
Aussehen der Stammfunktion (nicht gefragt)
Es gibt unendlich viele Stammfunktionen von f, wobei diese sich nur durch Verschiebung in y-Richtung unterscheiden. Eine mögliche Stammfunktion sieht so aus:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Du sollst den Zusammenhang zwischen dem Graphen von $f$ und dem Graphen seiner Stammfunktion F finden.
Dabei beschreibt $f$ das Monotonieverhalten von $G_{f}$ .
Monotonie/Globalverlauf: Untersuche, wann $G_{f}$ oberhalb/unterhalb der x-Achse verläuft.
Extremstellen: Untersuche, wo $G_{f}$ Nullstellen hat.
Wendepunkte: Untersuche, wo $G_{f}$ Extremstellen hat.

Lösen Sie die folgende Gleichung über der Grundmenge der reellen Zahlen.

$(e^{x})^{2} - 25 = 0$ (3 BE)

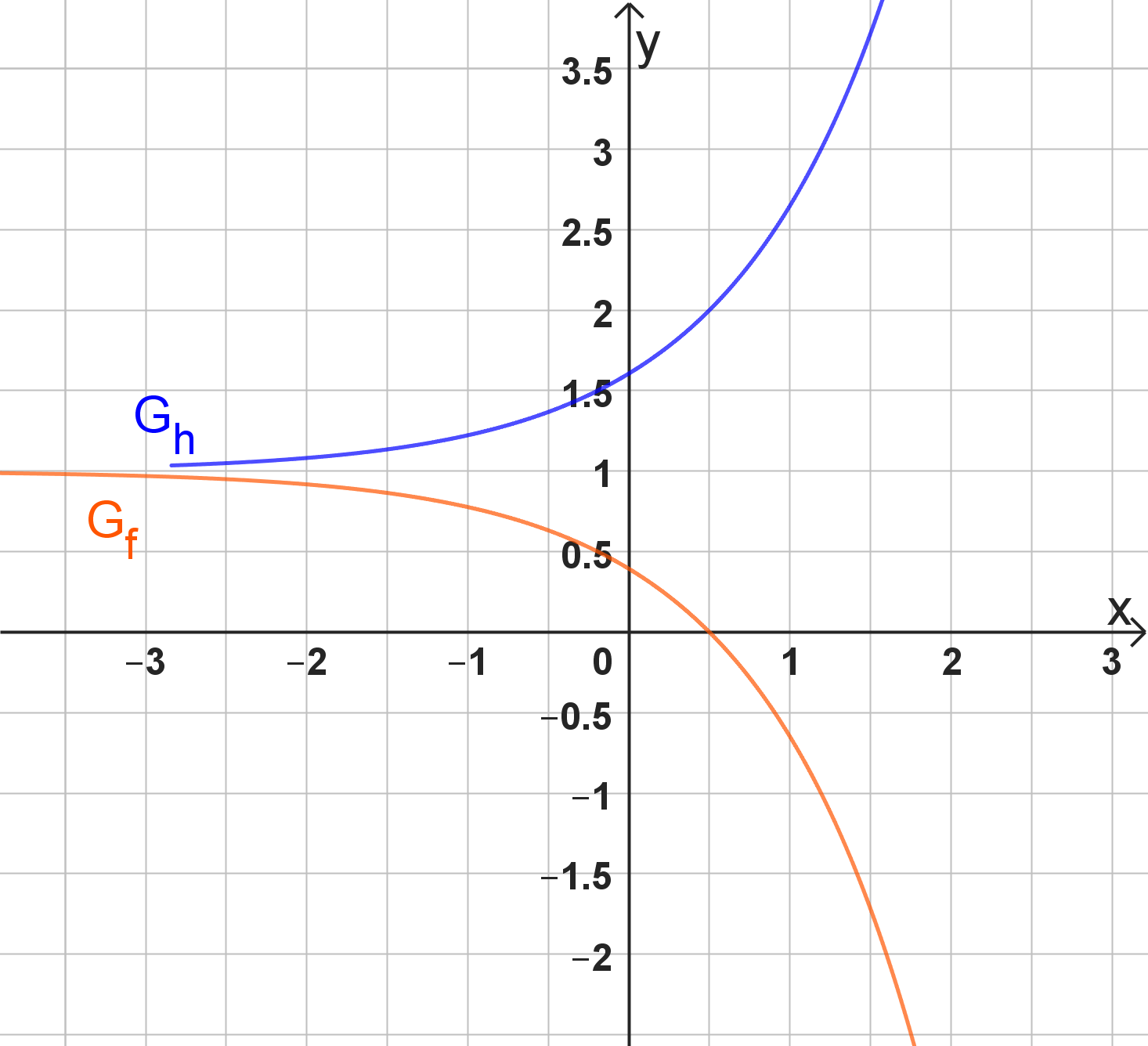
Die folgende Abbildung zeigt einen Ausschnitt des Graphen $G_{h}$ einer Exponentialfunktion h mit der Definitionsmenge $D_h=\R$ . Der zugehörige Funktionsterm besitzt die Form $h(x)=e^{x+d}+y_0$ mit $d,y_0\in\R$ .

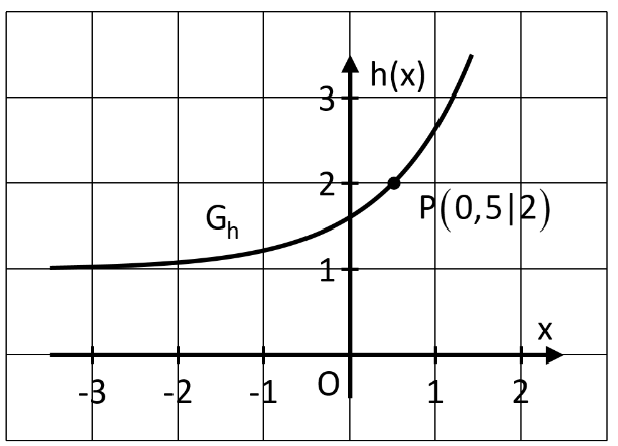
Bestimmen Sie mithilfe der obigen Abbildung nachvollziehbar die Werte der Parameter d und $y_{0}$ . (3 BE)

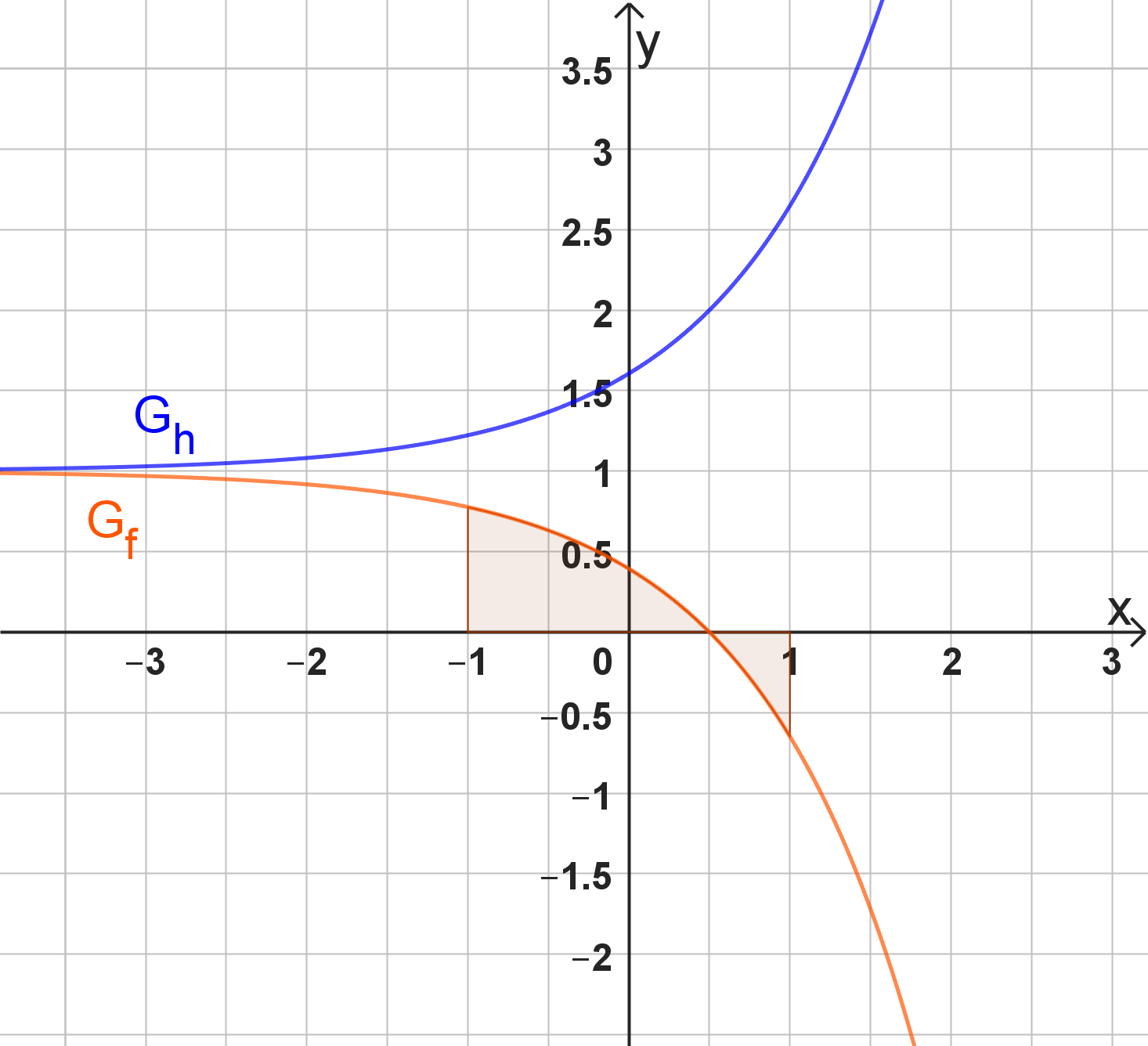
Entscheiden Sie anhand des Graphen der Funktion h, ob die nachfolgende Aussage wahr oder falsch ist. Veranschaulichen Sie Ihre Überlegung dazu in der Abbildung unter 4.0
$\int_{-1}^1(2-h(x))dx>0$
(2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
Verschiebung und Spiegelung von $G_{h}$
Skizziere den Graph der Funktion
$f(x)=2-h(x)=2-(e^{x-0{,}5}+1)=1-e^{x-0{,}5}$
Er hat die gleiche Asymptote wie $G_{h}$ und wurde an $y_{0} = 1$ gespiegelt:
Betrachtung der Teilflächen
Zeichne die Teilflächen von $x = - 1$ bis $x = 1$ ein:
Da die linke Teilfläche, die oberhalb der x-Achse liegt, größer ist als die rechte, ist die Flächenbilanz positiv. Die Aussage $\int_{-1}^1(2-h(x))dx>0$ wahr.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Überlege dir zuerst, wie die Funktion $f (x) = 2 - h (x)$ aussieht.
Markiere anschließend die Teilflächen und untersuche, welche größer ist.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle g'\left(x\right)$	$=$	$\displaystyle 0$
$\displaystyle -x^3+4x$	$=$	$\displaystyle 0$
	↓	Du kannst x ausklammern.
$\displaystyle x\left(-x^2+4\right)$	$=$	$\displaystyle 0$

$\displaystyle \left(e^x\right)^2-25$	$=$	$\displaystyle 0$	$\displaystyle +25$
$\displaystyle \left(e^x\right)^2$	$=$	$\displaystyle 25$
	↓	Ziehe die Wurzel. Beachte, dass es zwei Lösungen gibt.
$\displaystyle e^x$	$=$	$\displaystyle \pm5$

$\displaystyle 2$	$=$	$\displaystyle e^{0{,}5+d}+1$	$\displaystyle -1$
$\displaystyle 1$	$=$	$\displaystyle e^{0{,}5+d}$
	↓	Verwende den natürlichen Logarithmus ln
$\displaystyle \ln\left(1\right)$	$=$	$\displaystyle 0{,}5+d$
	↓	Es gilt $l n (1) = 0$
$\displaystyle 0$	$=$	$\displaystyle 0{,}5+d$	$\displaystyle -0{,}5$
$\displaystyle -0{,}5$	$=$	$\displaystyle d$

Teil 1 Analysis

Symmetrieuntersuchung

Eingeschränkte Definitionsmenge

Hast du eine Frage oder Feedback?

Ableitung bestimmen

Nullstellen der Ableitung

Hast du eine Frage oder Feedback?

Funktionsterm aufstellen

bestimmtes Integral

Hast du eine Frage oder Feedback?

Monotonieverhalten

Extremstellen

Globalverlauf von $G_{F}$

Wendestelle

Aussehen der Stammfunktion (nicht gefragt)

Hast du eine Frage oder Feedback?

Asymptote $y_{0}$

Parameter d

Hast du eine Frage oder Feedback?

Verschiebung und Spiegelung von $G_{h}$

Betrachtung der Teilflächen

Hast du eine Frage oder Feedback?

$\displaystyle 0$	$=$	$\displaystyle -x^2+4$
$\displaystyle x^2$	$=$	$\displaystyle 4$
	↓	Ziehe die Wurzel. Beachte, dass es zwei Lösungen gibt.
$\displaystyle x_2$	$=$	$\displaystyle 2$
$\displaystyle x_3$	$=$	$\displaystyle -2$

$\displaystyle e^x$	$=$	$\displaystyle 5_{ }$
	↓	ln
$\displaystyle x$	$=$	$\displaystyle \ln\left(5\right)$

Teil 1 Analysis

Symmetrieuntersuchung

Eingeschränkte Definitionsmenge

Hast du eine Frage oder Feedback?

Ableitung bestimmen

Nullstellen der Ableitung

Hast du eine Frage oder Feedback?

Funktionsterm aufstellen

bestimmtes Integral

Hast du eine Frage oder Feedback?

Monotonieverhalten

Extremstellen

Globalverlauf von GFG_FGF​

Wendestelle

Aussehen der Stammfunktion (nicht gefragt)

Hast du eine Frage oder Feedback?

Asymptote y0y_0y0​

Parameter d

Hast du eine Frage oder Feedback?

Verschiebung und Spiegelung von GhG_hGh​

Betrachtung der Teilflächen

Hast du eine Frage oder Feedback?

Globalverlauf von $G_{F}$

Asymptote $y_{0}$

Verschiebung und Spiegelung von $G_{h}$