Wahlteil

1
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
In Braunschweig steht ein kugelförmiger Gasspeicher. Die Kugel hat einen Außenradius von $r=13{,}5 \mathrm{~m}$ .
1. Berechne die Oberfläche der Kugel.
  [2 Pkte]
2. Der Pfeil zeigt auf einen Ring, der kreisförmig um die Mitte des Gasspeichers verläuft. Der Ring ist $90\m$ lang.
  Berechne den Abstand zwischen dem Gasspeicher und dem Ring.
  [3 Pkte]
3. Für Reparaturarbeiten am Gasspeicher wird ein Kran aufgestellt.
  Berechne die Länge $x$ .
  [2 Pkte]
4. Die Metallwand des Gasspeichers ist $0{,}03 \mathrm{~m}$ dick.
  Berechne das Volumen des Hohlraums der Kugel.
  [2 Pkte]
5. In einer anderen Stadt steht ein weiterer kugelförmiger Gasspeicher, der einen doppelt so großen Durchmesser hat.
  Begründe, dass dieser Gasspeicher ein achtmal so großes Volumen besitzt.
  [1 Pkt]
2
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Ein Boiler dient zur Erwärmung von Wasser in Küche und Bad.
Wenn der Boiler eingeschaltet wird, erhöht sich die Wassertemperatur pro Minute um $15^{\circ} \mathrm{C}$ .
1. Zu Beginn hat das Wasser im Boiler eine Temperatur von $20^{\circ} \mathrm{C}$ .
  Berechne die Wassertemperatur nach 3 Minuten.
  [1 Pkt]
2. Stelle die Funktionsgleichung zur Berechnung der Wassertemperatur in der Form $y=m \cdot x+b$ auf.
  [2 Pkte]
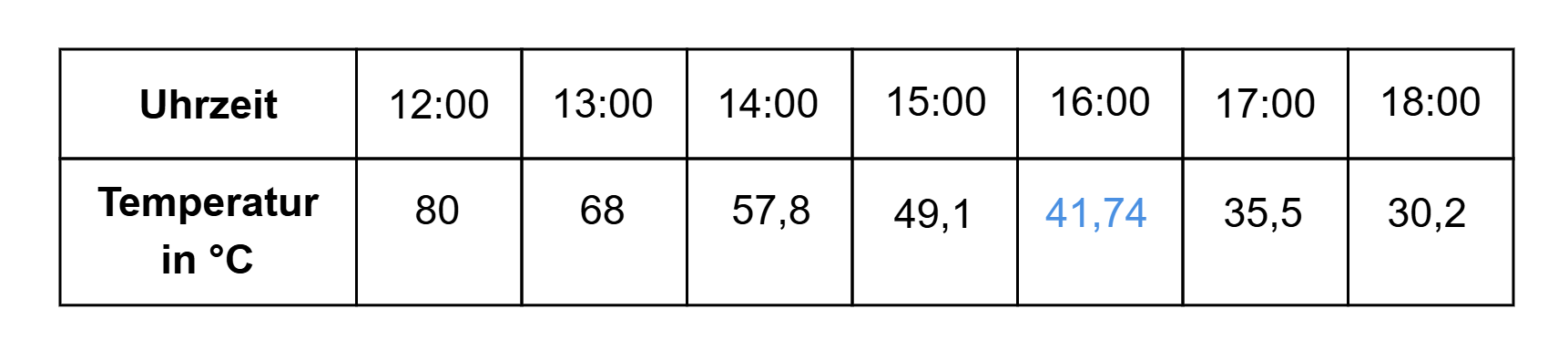
3. Nach Abschalten des Boilers um 12:00 Uhr fällt die Temperatur des Wassers pro Stunde um ca. $15 %$ .
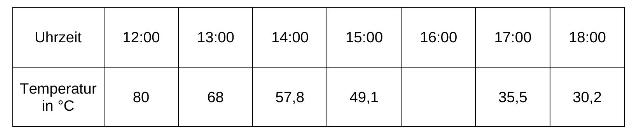
  Vervollständige die Tabelle.
  [1 Pkt]
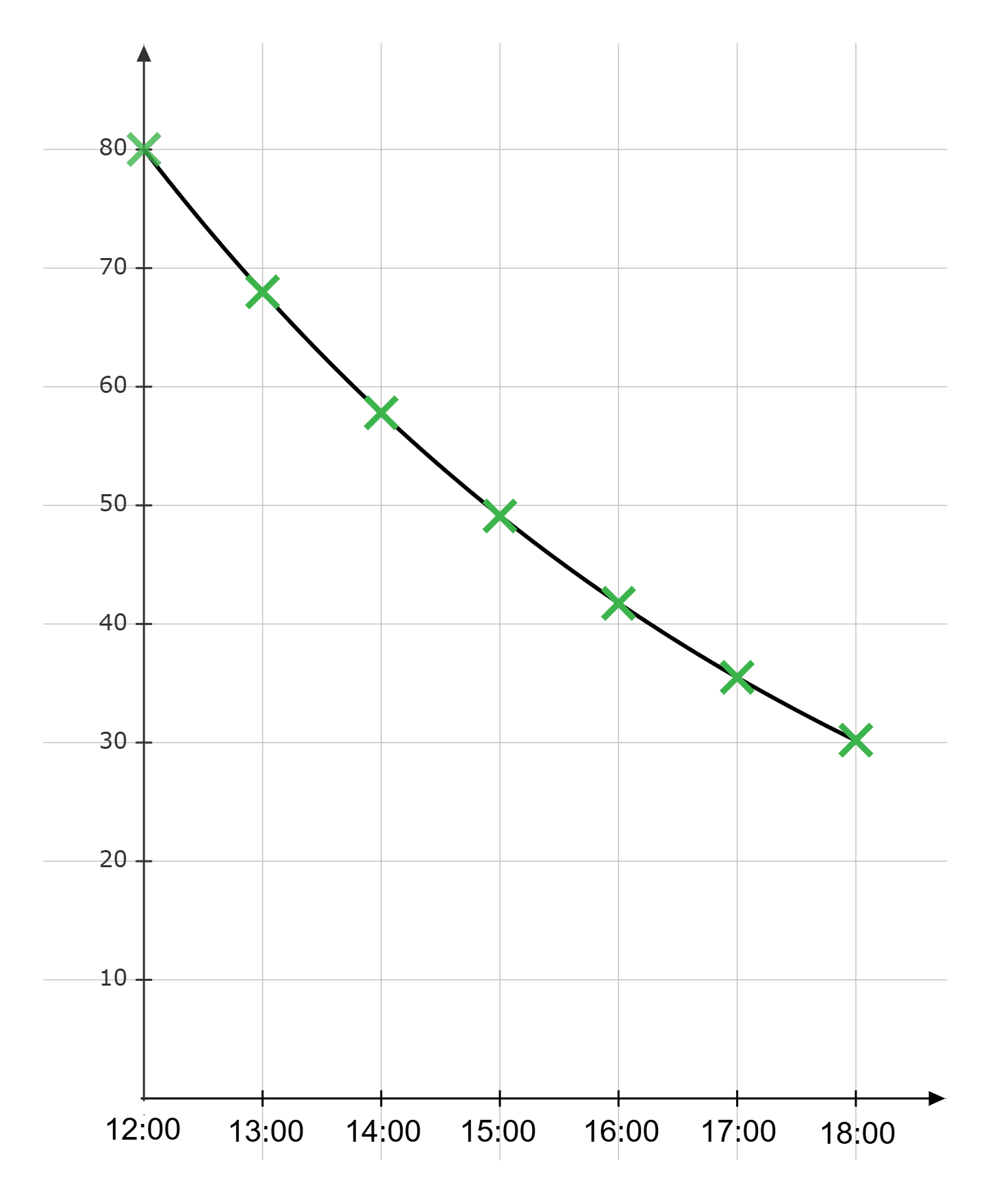
4. Zeichne die Wertepaare in das Koordinatensystem und verbinde sie sinnvoll.
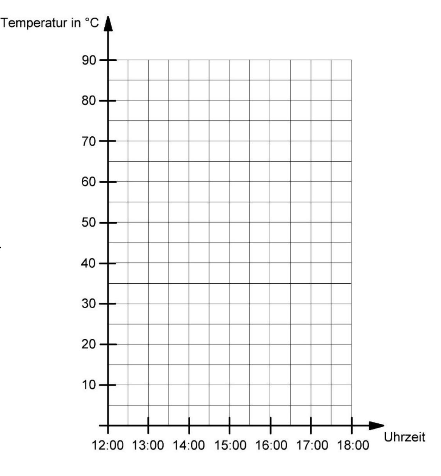
  Fülle die Lücken aus.
  Um 12:45 Uhr beträgt die Temperatur $\_\_\_\_\_\ ^\circ\text{C}$ .
  Um $______$ Uhr ist die Temperatur um $35^{\circ} \mathrm{C}$ gefallen.
  [5 Pkte]
5. Kreuze an.
  Die im Graph dargestellte Zuordnung ist...
  [1 Pkt]
  linear.
  proportional.
  exponentiell.
3
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Pia und Lea trinken gern Tee.
Sie haben diese Teebeutel unsortiert in einer Teebox:
- 10 Beutel Kamillentee (K)
- 4 Beutel Erdbeertee (E)
- 6 Beutel Apfeltee (A)
1. Pia greift, ohne hinzusehen, in die Teebox und zieht nacheinander zwei Teebeutel heraus.
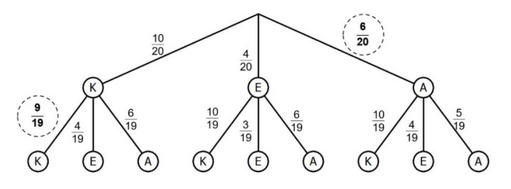
  Ergänze im Baumdiagramm die fehlenden Wahrscheinlichkeiten.
  [2 Pkte]
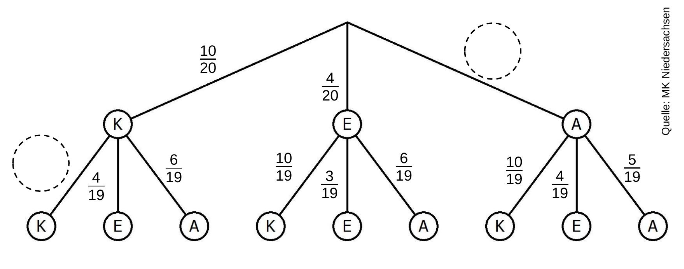
2. Berechne die Wahrscheinlichkeit, dass Pia erst Kamillentee und dann Apfeltee zieht.
  [2 Pkte]
3. Pia und Lea mögen keinen Erdbeertee.
  Berechne die Wahrscheinlichkeit, dass Pia keinen Erdbeertee zieht.
  [3 Pkte]
4. Lea berechnet die Wahrscheinlichkeit für ein Ereignis mit der folgenden Rechnung:
  $P=1-\left(\dfrac{4}{20} \cdot \dfrac{3}{19}\right)$
  Gib das passende Ereignis an.
  [2 Pkte]
5. Pia hat ein Glücksrad gebaut und behauptet: „Statt zweimal aus der Teebox zu ziehen, können wir auch zweimal am Glücksrad drehen."
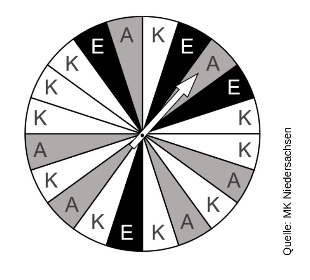
  Begründe, dass das Glücksrad nicht zum Baumdiagramm aus Aufgabenteil a) passt.
  [1 Pkt]
4
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Die Bergbahn „Waldi" fährt von einer Talstation zu einer Bergstation. Danny hat eine Skizze gezeichnet und einige Streckenlängen eingetragen.
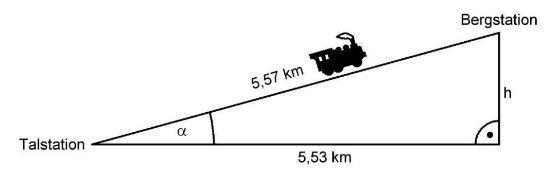
1. Berechne den Höhenunterschied $h$ .
  [2 Pkte]
2. Berechne die Größe des Steigungswinkels $\alpha$ .
  [2 Pkte]
3. Die Bergbahn „Rosi" hat eine Steigung von $9 %$ .
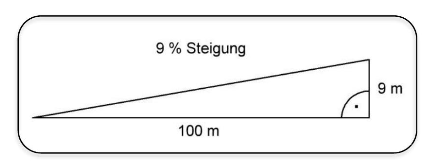
  Entscheide mithilfe einer Rechnung, welche Bergbahn die größere Steigung hat.
  [3 Pkte]
4. Danny behauptet: „Die Steigung einer Strecke kann höchstens $100 \%$ betragen."
  Zeige, dass Dannys Behauptung falsch ist.
  [1 Pkt]
5. Damit Züge in Kurven schneller fahren können, werden die Gleise etwas geneigt. Die maximale Geschwindigkeit hängt vom Neigungswinkel $\alpha$ ab.
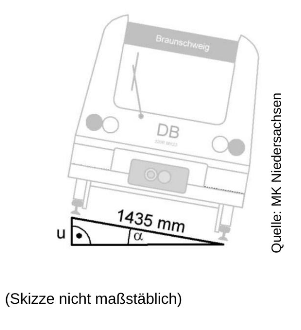
  Bestimme die maximale Geschwindigkeit, mit der ein Zug bei einem Höhenunterschied von $u = 217$ mm durch die Kurve fahren darf.
  $\def\arraystretch{2} \renewcommand{\arraystretch}{2} \begin{array}{c|c} \text{Neigungswinkel\ } \alpha & \text{max. Geschwindigkeit} \\ \hline 0^\circ \text{\ bis\ } 4{,}3^\circ & 60\ \dfrac{\text{km}}{\text{h}} \\ \hline \text{über\ }4{,}3^\circ \text{\ bis\ } 8{,}6^\circ & 80\ \dfrac{\text{km}}{\text{h}} \\ \hline \text{über\ } 8{,}6^\circ & 90\ \dfrac{\text{km}}{\text{h}} \end{array}$
  [2 Pkte]

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?