Teil 2
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
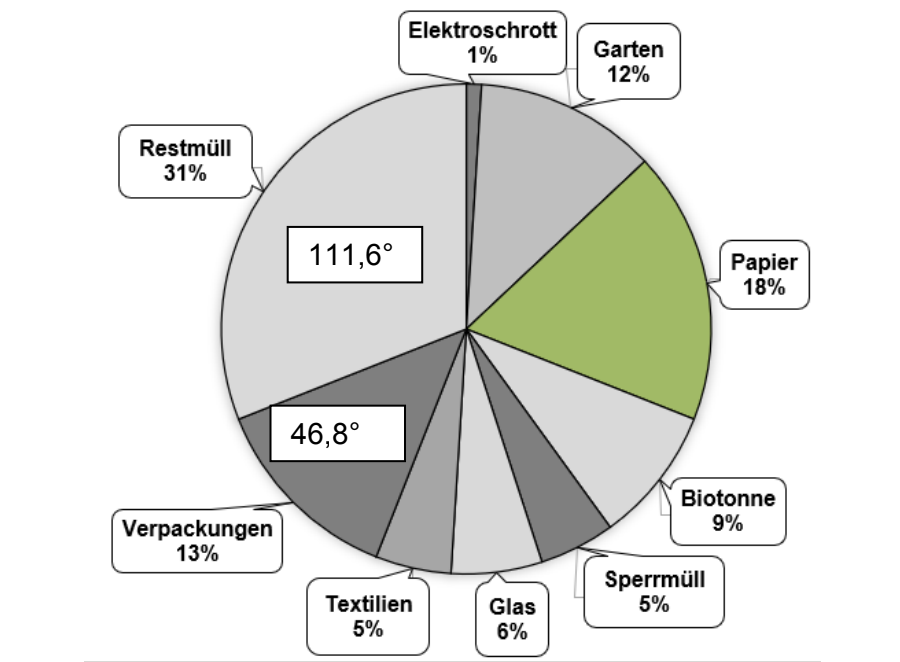
Im Jahr 2015 fielen in Deutschland insgesamt Millionen Tonnen Hausmüll an.
Zu diesem Zeitpunkt lebten in Deutschland ca. Millionen Menschen.
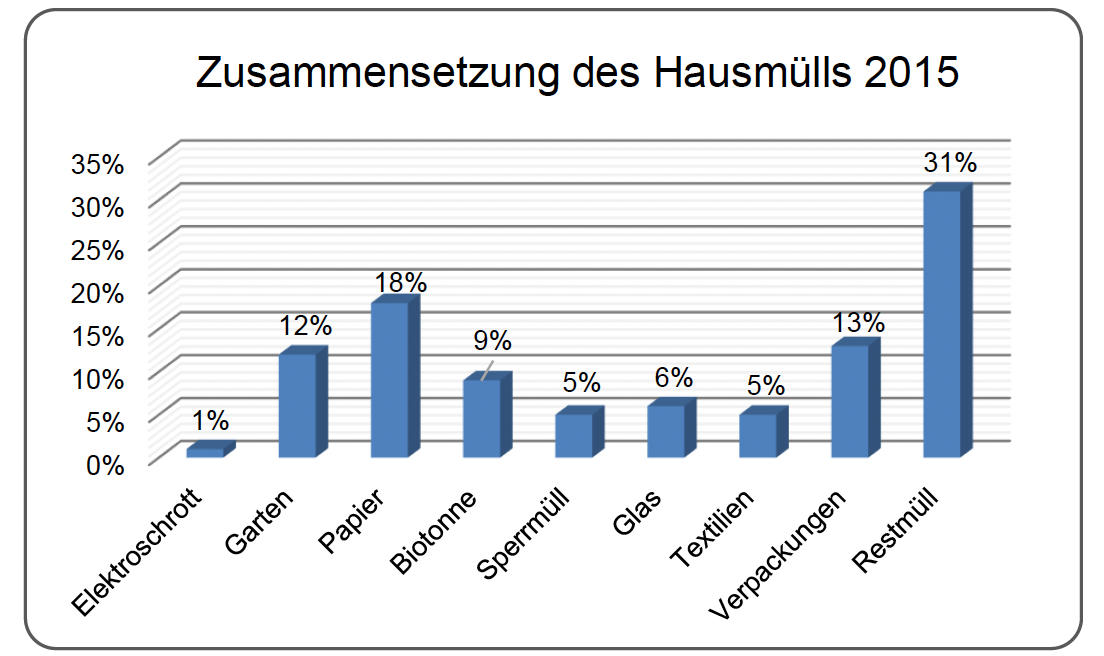
Berechne, wie viele Tonnen Hausmüll jede Person in Deutschland durchschnittlich verursacht hat.
[ 1 Pkt ]
Berechne, wie viele Tonnen Papier im Hausmüll enthalten waren.
[ 2 Pkte ]
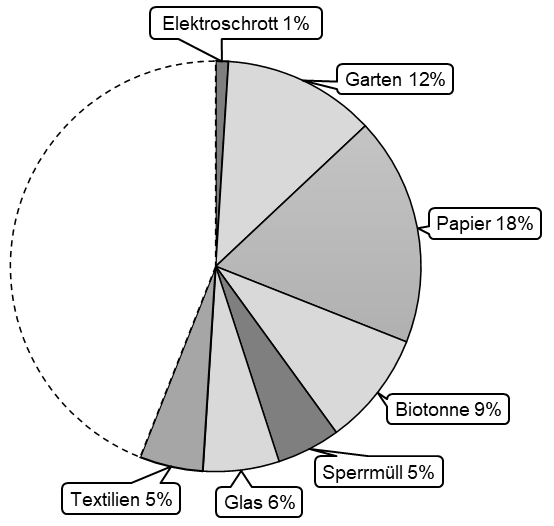
Vervollständige das Kreisdiagramm.
[ 2 Pkte ]
- 2
Zum 14. Geburtstag ihres Enkels Erik legt Oma Ingrid ein Führerscheinkonto bei der Bank an. Sie zahlt ein. Die Bank verzinst dieses Geld mit einem jährlichen Zinssatz von . Bis zu Eriks 17. Geburtstag gibt es keine weiteren Ein- und Auszahlungen.
Berechne das Kapital, das Erik an seinem 17. Geburtstag ausgezahlt bekommt.
[ 2 Pkte ]
- 3
In einem Café soll ein großes Schild als Dekoration an die Wand gehängt werden.
Der Durchmesser des Schildes beträgt .

Berechne den Flächeninhalt des Schildes.
[ 1 Pkt ]
Um den Rand des Schildes soll eine LED-Lichterkette angebracht werden.
Überprüfe, ob eine lange LED-Lichterkette dafür ausreicht.
[ 2 Pkte ]
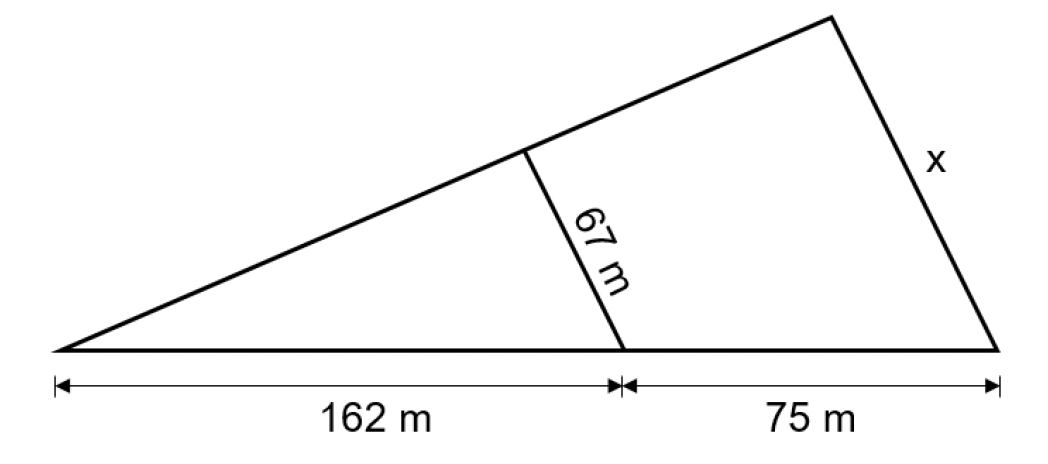
- 4
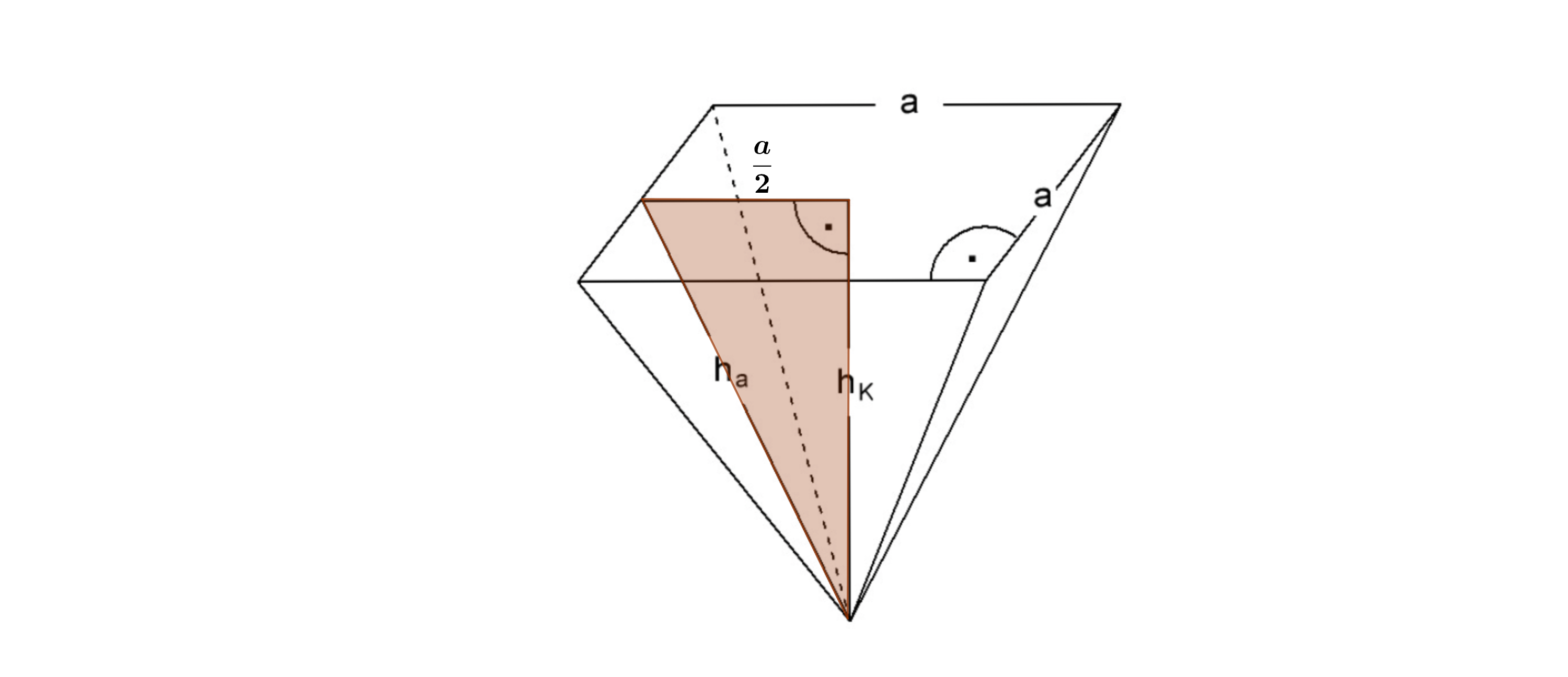
Abgebildet ist ein Werkstück aus Kunststoff.
Berechne die Seitenlänge des Werkstücks.
[ 3 Pkte ]
Das Werkstück wird von außen abgeschliffen.
Berechne die zu schleifende Fläche.
(Solltest du die Teilaufgabe a) nicht gelöst haben, rechne mit weiter.)
[ 2 Pkte ]
- 5
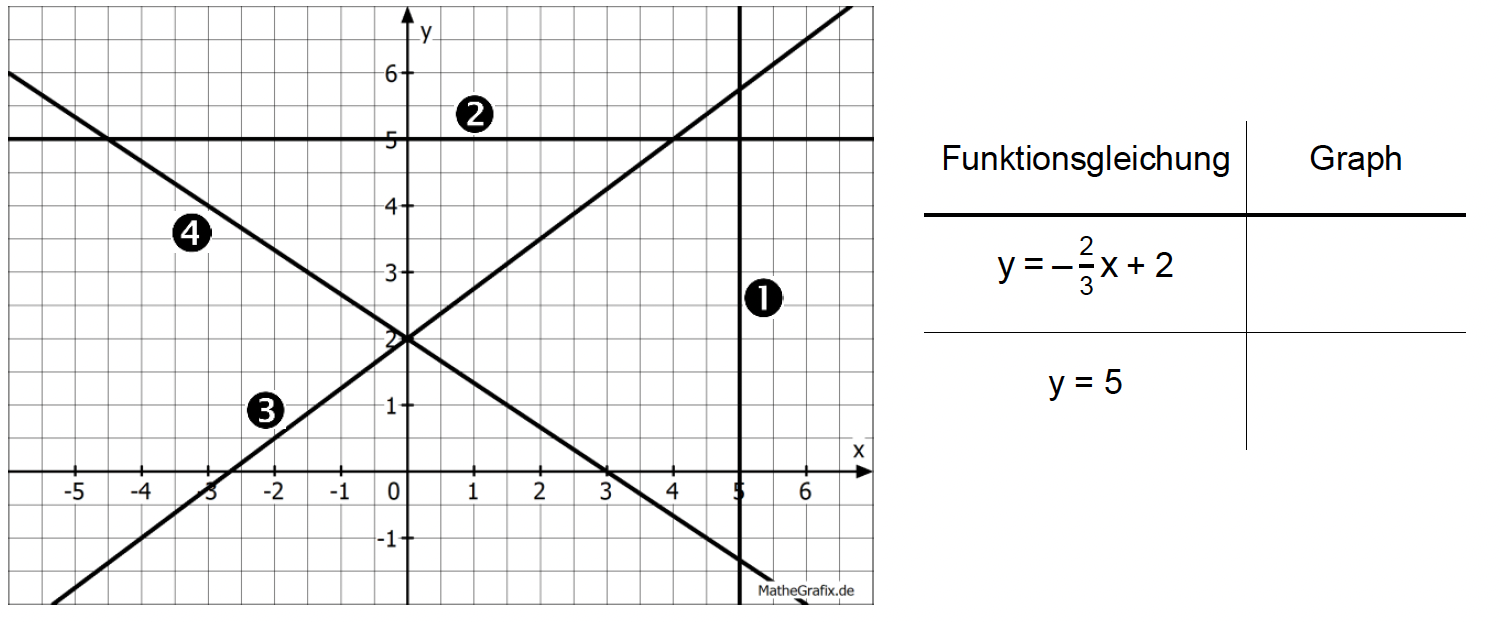
Ordne den Funktionsgleichungen den passenden Graphen zu.
[ 2 Pkte ]
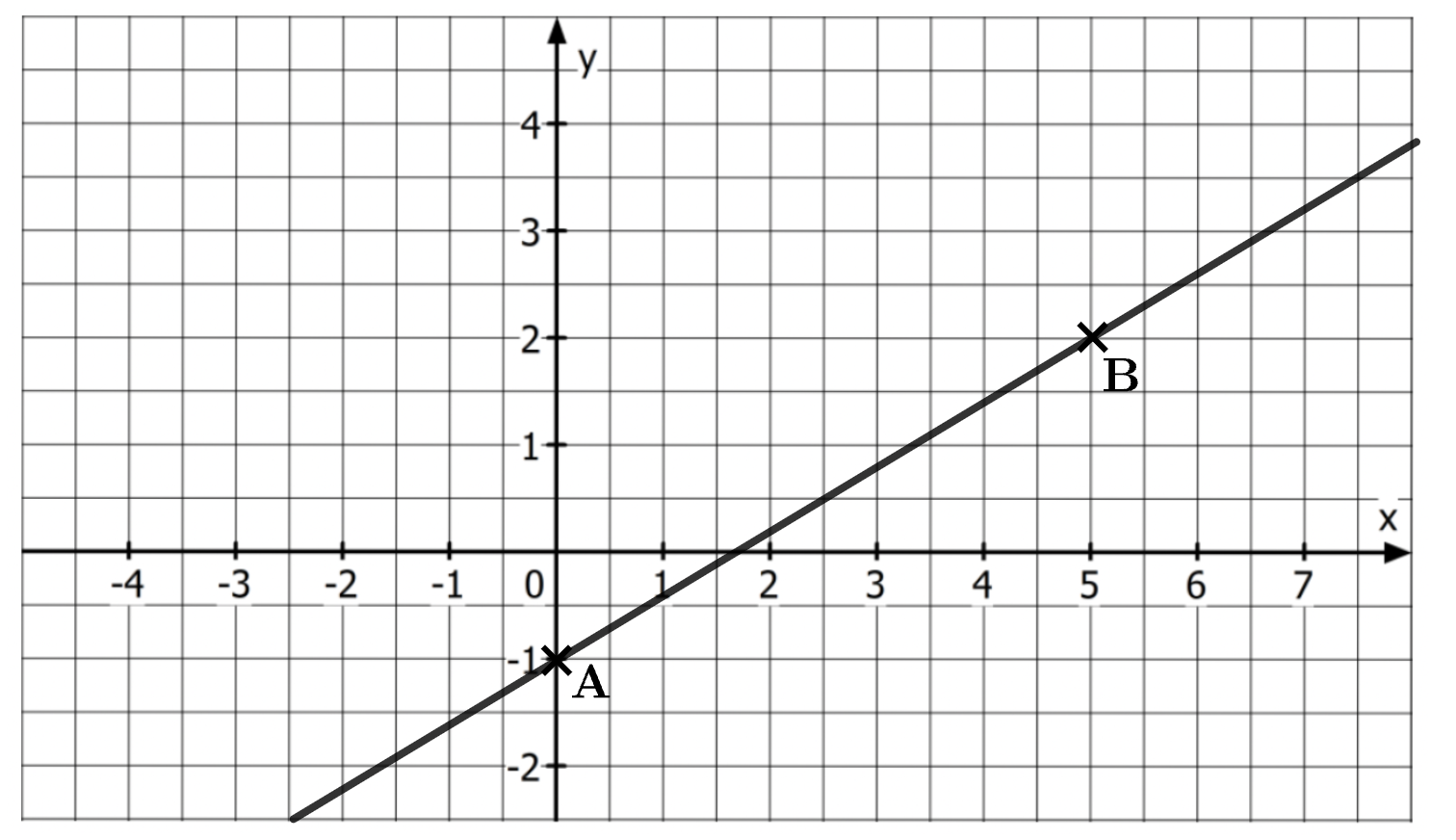
Durch die Punkte und verläuft eine Gerade.
Trage die Punkte und in das Koordinatensystem ein und zeichne die Gerade.
[ 1 Pkt ]
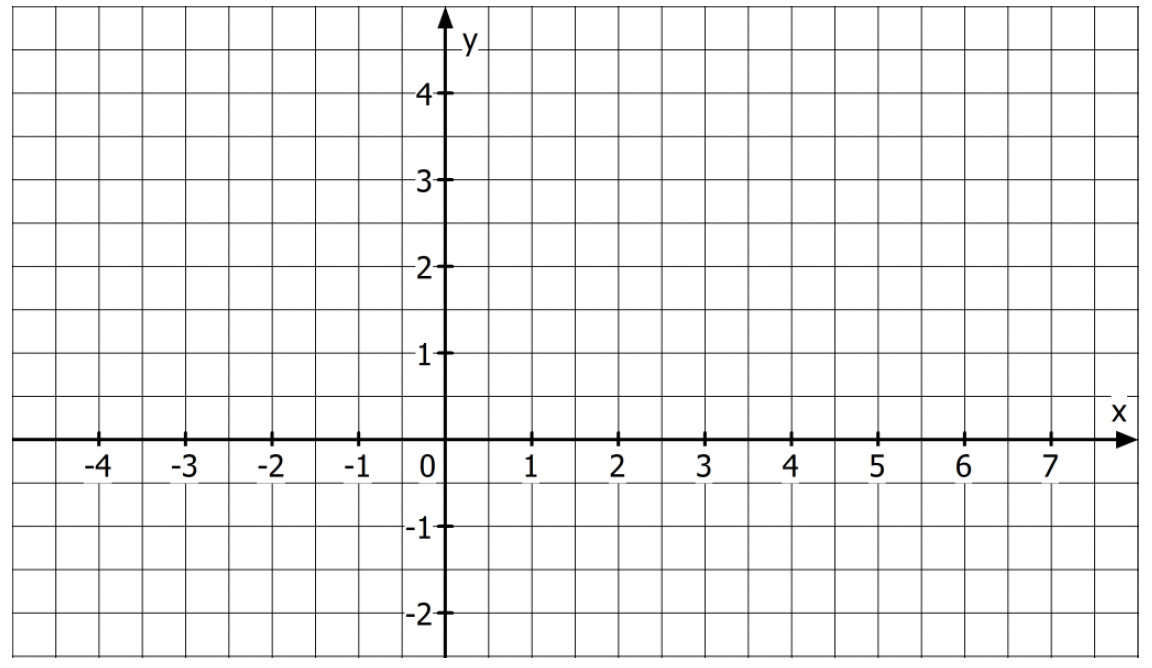
Bestimme die Funktionsgleichung der Geraden.
[ 2 Pkte ]
Zwei andere Geraden und haben folgende Funktionsgleichungen:
Bestimme den Schnittpunkt der beiden Geraden.
[ 3 Pkte ]
- 6
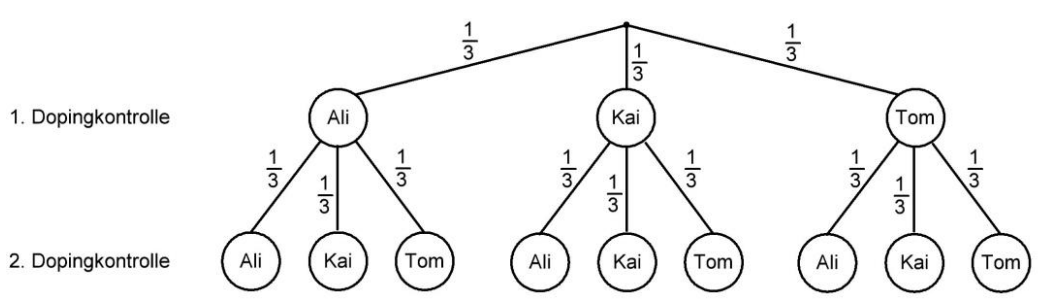
Drei Radrennfahrer (Ali, Kai und Tom) fahren ein Radrennen.
Das Radrennen besteht aus zwei Etappen.
Nach jeder Etappe wird ein Radrennfahrer zur Dopingkontrolle zufällig ausgelost.
Vervollständige das Baumdiagramm und schreibe die Wahrscheinlichkeiten an die Äste.
[ 2 Pkte ]
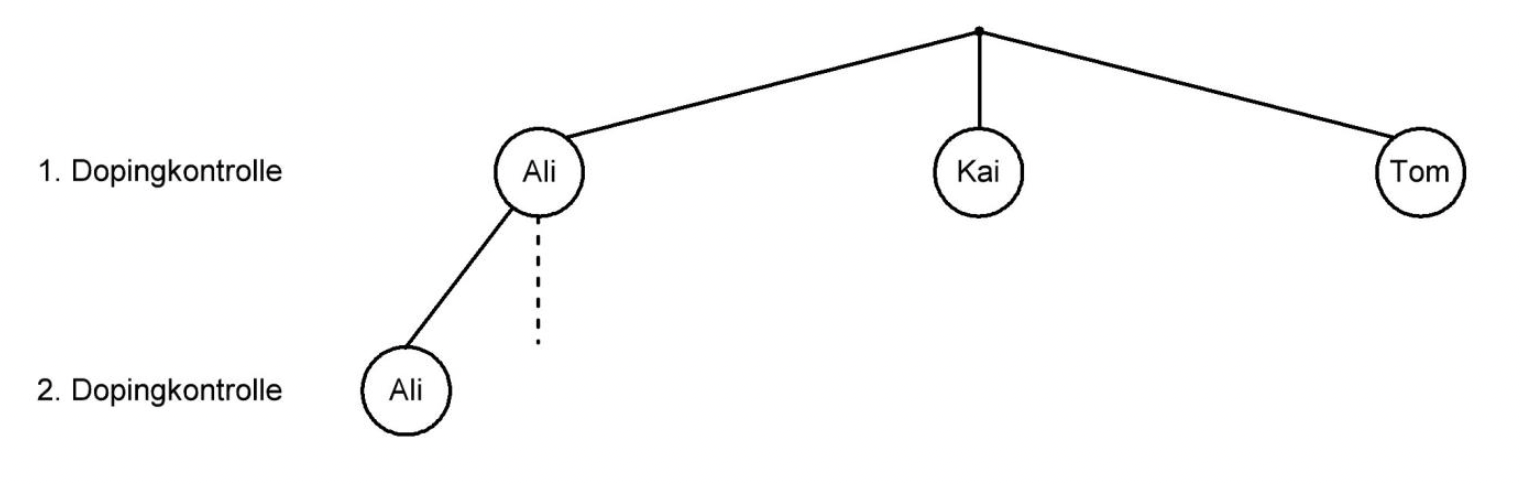
Berechne die Wahrscheinlichkeit, dass zweimal derselbe Radrennfahrer ausgelost wird.
[ 2 Pkte ]
- 7
Lea möchte ein Klassenfoto aufnehmen. Sie stellt sich mit ihrer Kamera mittig vor die Klasse.
Berechne den Abstand , den Lea benötigt, um die gesamte Klasse aufs Foto zu bekommen.
[ 3 Pkte ]
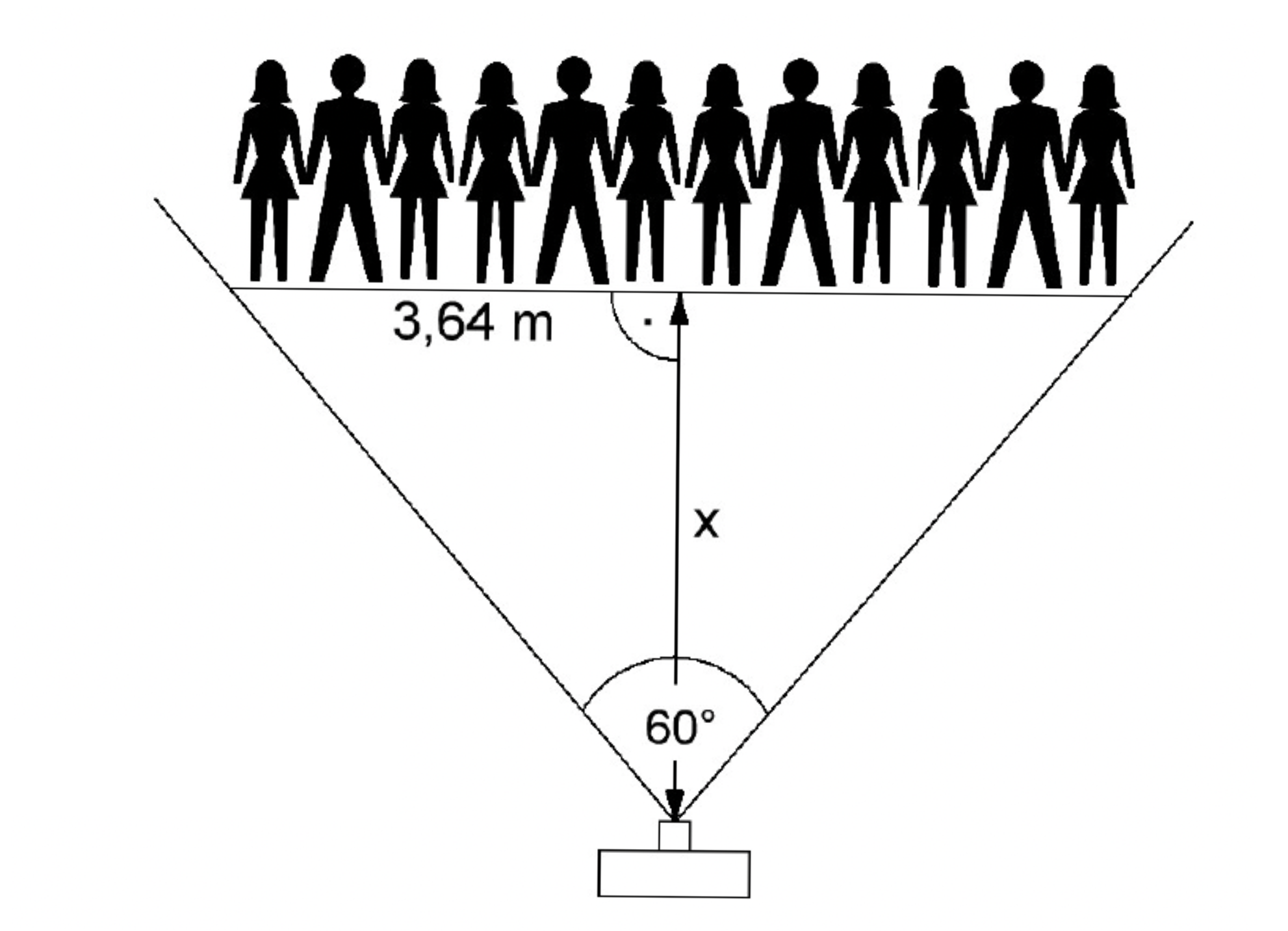
(Skizze nicht maßstäblich)
- 8
Eine Regentonne hat ein Fassungsvermögen von Litern.
Sie ist bis unter den Rand mit Wasser gefüllt.
Berechne die Höhe h des Wasserstandes in der Tonne.
[ 3 Pkte ]
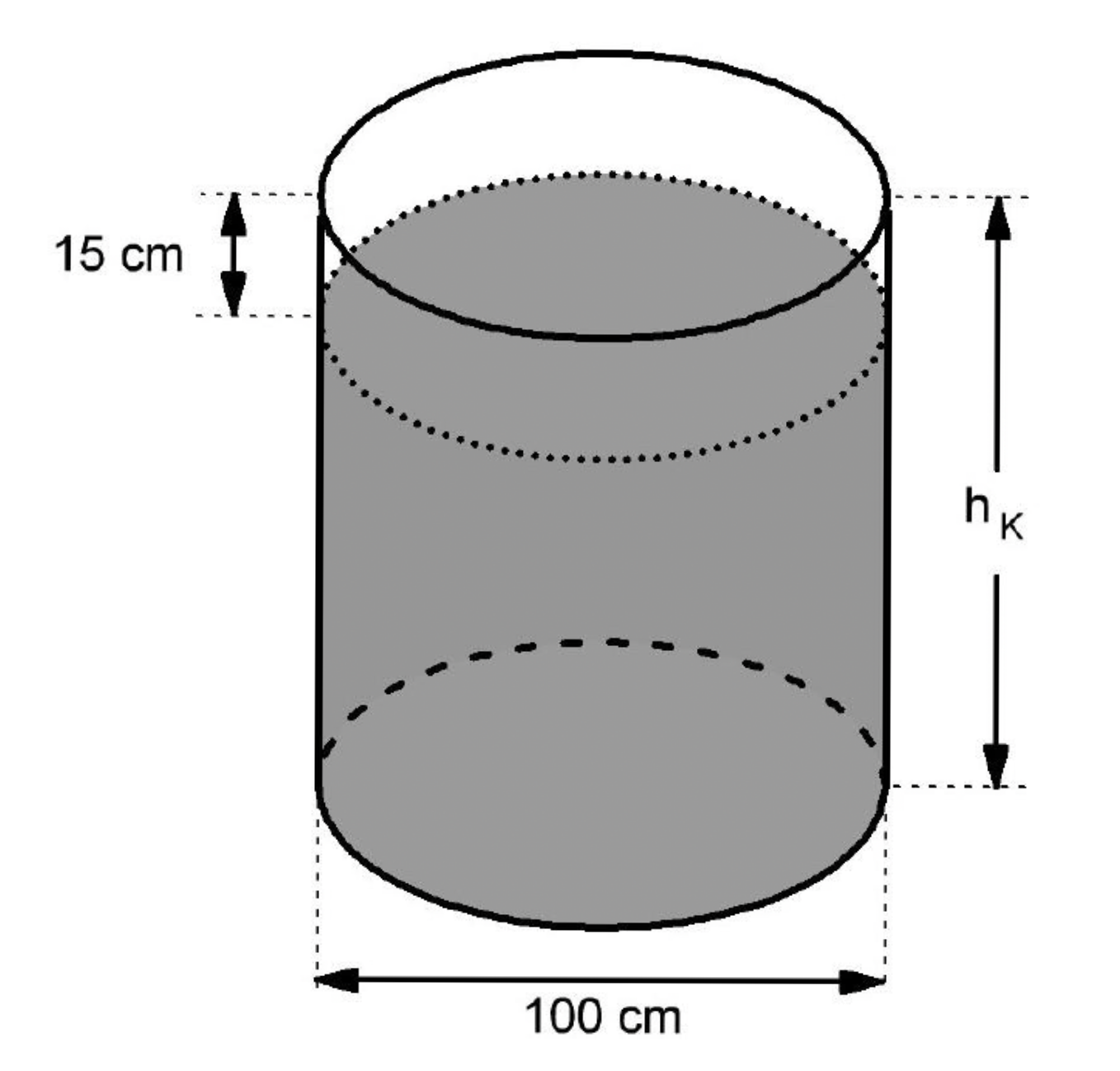
(Skizze nicht maßstäblich)
- 9
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?