Aufgaben zu Oberfläche und Volumen von Würfel und Quader

1
Die nicht maßstabsgetreue Skizze zeigt einen Quader und dessen Abmessungen. Berechne die Oberfläche des Quaders.
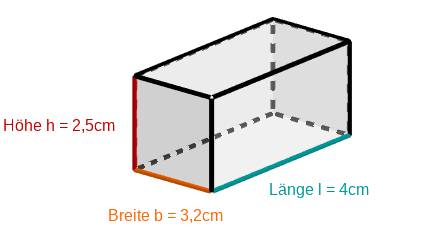cm²

Für diese Aufgabe benötigst Du folgendes Grundwissen: Oberfläche des Quaders
$l=4\,\mathrm{cm}$
$b=3{,}2\,\mathrm{cm}$
$h=2{,}5\,\mathrm{cm}$
Für die Oberfläche eines Quaders gilt:
$O_\mathrm{Quader}=2\cdot\left(l\cdot b+l\cdot h+b\cdot h\right)$
Berechne die Deck- und Grundfläche: $\left[2\cdot\left(l\cdot b\right)\right]$
$2\cdot\left(4\,\mathrm{cm}\cdot3{,}2\,\mathrm{cm}\right)=25{,}6\,\mathrm{cm}^2$
Berechne die Vorder- und Rückfläche: $\left[2\cdot\left(h\cdot b\right)\right]$
$2\cdot\left(3{,}2\,\mathrm{cm}\cdot2{,}5\,\mathrm{cm}\right)=16\,\mathrm{cm}^2$
Berechne die Seitenflächen: $\left[2\cdot\left(l\cdot h\right)\right]$
$2\cdot\left(4\,\mathrm{cm}\cdot2{,}5\,\mathrm{cm}\right)=20\,\mathrm{cm}^2$
Berechne die Oberfläche als Summe der vorher bestimmten Werte.
$O_\mathrm{Quader}=25{,}6\,\mathrm{cm}^2+20\,\mathrm{cm}^2+16\,\mathrm{cm}^2=61{,}6\,\mathrm{cm}^2.$
$\;\;\Rightarrow\;\;$ Die Oberfläche des Quaders beträgt $61{,}6\,\mathrm{cm}^2$ .

Ein rechteckiger Wasserbehälter mit den Maßen $0{,}8\,\mathrm{m}\cdot0{,}45\,\mathrm{m}\cdot1{,}5\,\mathrm{m}$ soll mit Wasser gefüllt werden.

Wie viel Liter kann er fassen?

Aus einem Draht von einem Meter Länge wurde das Kantenmodell eines Würfels gebaut. Es blieb ein Reststück von 4,0 cm. Wie lang ist eine Würfelkante?

4
Beim Transport von Gütern ist es sinnvoll, den Laderaum möglichst genau auszunutzen. Für welches Volumen an Gütern ist der LKW aus dem Bild gebaut?
Der Durchmesser eines Rades beträgt etwa $100\,\mathrm{cm}$ und die Frontscheibe ist $2{,}50\,\mathrm m$ breit.
Wie viel Liter Wasser könnte man mit dem LKW aus dem Bild transportieren?
Kann man dasselbe Volumen auch mit Tischen und Stühlen komplett ausfüllen?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quader
Tipp: Benutze den Raddurchmesser für Höhe und Länge des Laderaumes, der die Form eines Quaders hat.
Vorüberlegungen
Berechne das Volumen des Laderaums. Du siehst, dass der Laderaum ein Quader ist. Für sein Volumen benötigst Du also die drei Kantenlängen Höhe $h$ , Länge $l$ und Breite $b$ des Quaders.
Schätzen der Maße
Du erkennst , dass der Quader etwa 3 Räder hoch und 5 Räder lang ist. Ein Rad hat einen Durchmesser von $100\, \textrm{cm}= 1\,\text{m}$ .
=> $h=3m; l=5m$
Berechnung durch Angabe
Der Quader ist in etwa so breit wie die Frontscheibe.
=> $b=2{,}5m$
Berechnung des Volumens
Die Volumenformel für den Quader lautet: $V=l\cdot b\cdot h$
$V=5m\cdot 2{,}5m\cdot 3m= 37{,}5m³$
Anwendungen
Wenn man den Laderaum mit Wasser füllen würde, könnte man 37,5m³, also 37500 Liter transportieren.
Tische und Stühle passen nicht lückenlos ineinander, sodass Du weniger Material unterbringen kannst. Deshalb musst Du Dir beim Packen nicht nur überlegen, welche Maße die einzelnen Gegenstände haben, sondern auch, wie sie geschickt ineinander zu stapeln sind.
5
Die beiden Skizzen zeigen einen Quader und einen Würfel mit deren Abmessungen.
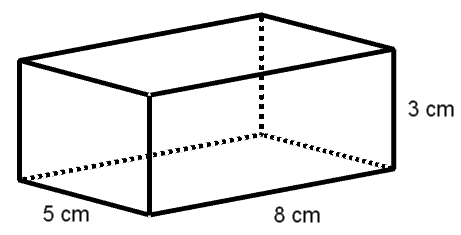
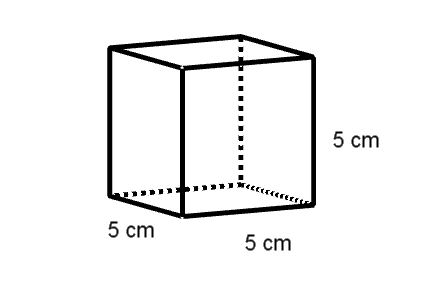
1. Welcher dieser beiden Körper hat den größeren Oberflächeninhalt?
  Der Würfel hat eine größere Oberfläche.
  Der Quader hat eine größere Oberfläche.
  Beide haben die gleiche Oberfläche.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt
  Tipp: Wenn du dir nicht sicher bist, wie die Formel für den Oberflächeninhalt eines Quaders lautet, überlege dir, welche Seitenflächen gleich sind und wie du diese jeweils berechnen kannst.
  Oberflächeninhalt
  Der Oberflächeninhalt beider Körper wird hier berechnet und anschließend verglichen.
  Oberfläche des Quaders
  Die Formel zur Berechnung der Oberfläche eines Quaders lautet:
  $O = 2\cdot l\cdot b + 2\cdot l \cdot h + 2\cdot b \cdot h$
  Für den Quader links sind:
  $l = 8\text{cm}$
  $b = 5\text{cm}$
  $h = 3\text{cm}$
  Diese Werte werden in die Formel eingesetzt:
  $\def\arraystretch{1.25} \begin{array}{lclclcl}O & = & 2\cdot 8\text{cm} \cdot 5\text{cm} & + & 2 \cdot 8\text{cm} \cdot 3\text{cm} & + & 2 \cdot 5\text{cm} \cdot 3\text{cm} \\& = & 80\text{cm}^2 & + & 48\text{cm}^2 & + & 30\text{cm}^2 \\& = & 158\text{cm}^2 \end{array}$
  Der Oberflächeninhalt des Quaders beträgt also $158\text{cm}^2$
  Oberfläche des Würfels
  Für den Würfel rechts ist die Kantenlänge $a = 5\text{cm}$ . Die Fläche $A$ einer Seite kann wie folgt berechnet werden:
  $\def\arraystretch{1.25} \begin{array}{lcl}A & = & a \cdot a \\& = & 5\text{cm} \cdot 5\text{cm} \\& = & 25 \text{cm}^2\end{array}$
  Da bei einem Würfel alle $6$ Seitenflächen gleich groß sind, ergibt sich für die Oberfläche:
  $\def\arraystretch{1.25} \begin{array}{lcl}O & = & 6 \cdot 25\text{cm}^2 \\& = & 150\text{cm}^2 \end{array}$
  Der Oberflächeninhalt des Würfels beträgt also $150\text{cm}^2$ .
  Vergleich
  Der Oberflächeninhalt des linken Quaders $\left(158\text{cm}^2\right)$ ist größer als der Oberflächeninhalt des rechten Würfels $\left(150\text{cm}^2\right)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Oberfläche des Würfels mit der Formel $O=6\cdot a^2$ und die des Quaders mit $O = 2\cdot l\cdot b + 2\cdot l \cdot h + 2\cdot b \cdot h$ .
2. Welcher dieser beiden Körper hat das größere Volumen?
  Der Würfel hat ein größeres Volumen.
  Der Quader hat ein größeres Volumen.
  Beide haben das gleiche Volumen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Räumliche Figuren
  Volumen
  Das Volumen der beiden Körper wird hier berechnet, um beide Volumina vergleichen zu können.
  Volumen des Quaders
  Das Volumen eines Quaders lässt sich mit der folgenden Formel berechnen:
  $V = l\cdot b \cdot h$
  Aus der Skizze, oder aus Aufgabe (a), kannst du folgende Werte ablesen:
  $l = 8$ cm
  $b = 5$ cm
  $h = 3$ cm
  Diese Werte kannst du nun in die Formel einsetzen:
  $\def\arraystretch{1.25} \begin{array}{lcl}V & = & 8\text{cm} \cdot 5\text{cm} \cdot 3\text{cm} \\& = & 120\text{cm}^3 \end{array}$
  Das Volumen des Quaders links beträgt also $120\text{cm}^3$ .
  Volumen des Würfels
  Das Volumen eines Würfels lässt sich mit der folgenden Formel berechen:
  $V = a\cdot a\cdot a$
  Der Würfel aus der Skizze links hat eine Kantenlänge $a = 5$ cm. Diesen Wert kannst du nun in die Formel einsetzen:
  $\def\arraystretch{1.25} \begin{array}{lcl}V & = & 5\text{cm} \cdot 5\text{cm} \cdot 5\text{cm} \\& = & 125\text{cm}^3 \end{array}$
  Das Volumen des Würfels rechts beträgt also $125\text{cm}^3$ .
  Erkenntnis
  Der Quader hat somit ein kleineres Volumen $\left(120\text{cm}^3\right)$ als der Würfel $\left(125\text{cm}^3\right)$ , obwohl der Oberflächeninhalt des Quaders $\left(158\text{cm}^2\right)$ größer ist als der Oberflächeninhalt des Würfels $\left(150\text{cm}^2\right)$ .
  Eine Größere Oberfläche bedeutet also nicht zwingend ein größeres Volumen!
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne das Volumen des Würfels mit der Formel $V = a\cdot a\cdot a=a^3$ und das Volumen des Quaders mit $V = l\cdot b \cdot h$ .
6
Die Firma "Würfeldeluxe" hat eine Bestellung von $5000$ Würfel erhalten. Die Würfel sollen in einem rechteckigen Paket abgeschickt werden. Die Würfel haben alle eine Kantenlänge $a = 2 \,cm$ . Die Maße des Pakets kannst du in der Skizze ablesen. Passen alle Würfel in das Paket?
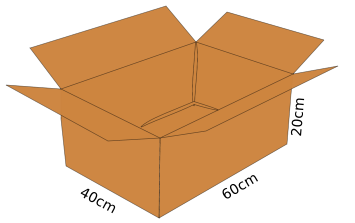
Ja, es passen alle Würfel ins Paket.
Nein, sie passen nicht ins Paket.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen des Quaders
Anzahl der Würfel in einer Reihe
Das Paket ist $60$ cm lang und ein Würfel hat eine Kantenlänge von $2$ cm. Um die Anzahl der Würfel in einer Reihe zu erhalten, teilst du die Länge der Reihe durch die Kantenlänge des Würfels:
$\def\arraystretch{1.25} \begin{array}{lcl}\text{Anzahl der Würfel in einer Reihe} & = & 60\text{cm} : 2\text{cm} \\& = & 30 \end{array}$
In eine Reihe passen also $30$ Würfel.
Anzahl der Würfel in einer Schicht
Das Paket ist $40$ cm breit. Die Anzahl der Reihen erhältst du, indem du die Breite des Pakets durch die Kantenlänge der Würfel teilst:
$\def\arraystretch{1.25} \begin{array}{lcl}\text{Anzahl der Reihen} & = & 40\text{cm} : 2\text{cm} \\& = & 20 \end{array}$
Es gibt also $20$ Reihen, in der sich jeweils $30$ Würfel befinden. Insgesamt erhältst du:
$\def\arraystretch{1.25} \begin{array}{lcl}\text{Anzahl der Würfel in einer Schicht} & = & 20 \cdot 30 \\& = & 600 \end{array}$
Es passen $600$ Würfel in eine Schicht.
Anzahl der Würfel im Paket
Das Paket ist $20$ cm hoch. Die Anzahl der Schichten erhältst du, indem du die Höhe des Pakets durch die Kantenlänge der Würfel teilst:
$\def\arraystretch{1.25} \begin{array}{lcl}\text{Anzahl der Schichten} & = & 20\text{cm} : 2\text{cm} \\& = & 10 \end{array}$
In das Paket passen $10$ Schichten, in jeder Schicht $600$ Würfel. Insgesamt ergibt sich also:
$\def\arraystretch{1.25} \begin{array}{lcl}\text{Anzahl der Würfel im Paket} & = & 10 \cdot 600 \\& = & 6000 \end{array}$
In ein Paket passen also $6000$ Würfel.
Die Firma "Würfeldeluxe" kann somit alle $5000$ Würfel in einem Paket abschicken.
Berechne, wie viele Würfel in das Paket passen. Sind es mehr als 6000?
7
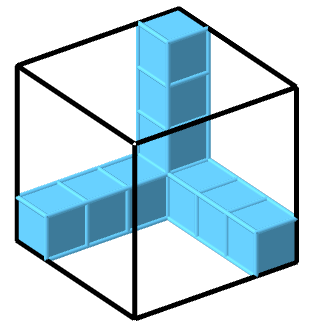
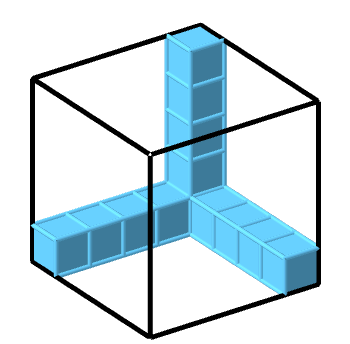
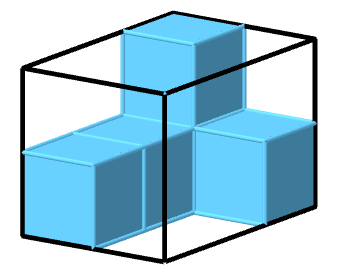
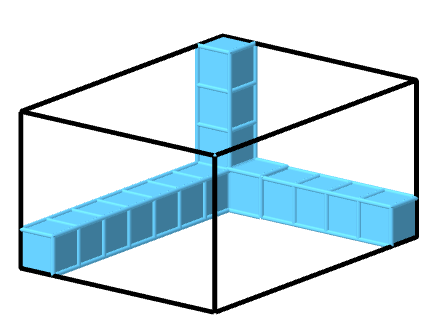
Bestimme die Anzahl der Einheitswürfel, die du benötigst, um den jeweiligen Körper vollständig auszufüllen.
1. 64 Einheitswürfel
  27 Einheitswürfel
  9 Einheitswürfel
  10 Einheitswürfel
  
  In einer Reihe zählst du $4$ Einheitswürfel.
  In einer Schicht gibt es $4$ Reihen mit jeweils $4$ Einheitswürfel. Insgesamt passen also $4 \cdot 4 = 16$ Einheitswürfel in eine Schicht.
  Im Würfel zählst du $4$ Schichten mit jeweils $16$ Einheitswürfel. Insgesamt passen somit $4 \cdot 16 = 64$ Einheitswürfel in den großen Würfel.
  Die Antwort " $64$ Einheitswürfel" ist also richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $125$ Einheitswürfel
  $100$ Einheitswürfel
  $64$ Einheitswürfel
  $150$ Einheitswürfel
  
  In einer Reihe zählst du $5$ Einheitswürfel.
  In einer Schicht gibt es $5$ Reihen mit jeweils $5$ Einheitswürfel. Insgesamt passen also $5 \cdot 5 = 25$ Einheitswürfel in eine Schicht.
  Im Würfel zählst du $5$ Schichten mit jeweils $25$ Einheitswürfel. Insgesamt passen somit $5 \cdot 25 = 125$ Einheitswürfel in den großen Würfel.
  Die Antwort " $125$ Einheitswürfel" ist also richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $12$ Einheitswürfel
  $11$ Einheitswürfel
  $8$ Einheitswürfel
  $6$ Einheitswürfel
  
  In einer Reihe zählst du $3$ Einheitswürfel.
  In einer Schicht gibt es $2$ Reihen mit jeweils $3$ Einheitswürfel. Insgesamt passen also $2 \cdot 3 = 6$ Einheitswürfel in eine Schicht.
  Im Quader zählst du $2$ Schichten mit jeweils $6$ Einheitswürfel. Insgesamt passen somit $2 \cdot 6 = 12$ Einheitswürfel in den Quader.
  Die Antwort " $12$ Einheitswürfel" ist also richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $192$ Einheitswürfel
  $216$ Einheitswürfel
  $160$ Einheitswürfel
  $168$ Einheitswürfel
  
  In einer Reihe zählst du $8$ Einheitswürfel.
  In einer Schicht gibt es $6$ Reihen mit jeweils $8$ Einheitswürfel. Insgesamt passen also $6 \cdot 8 = 48$ Einheitswürfel in eine Schicht.
  Im Quader zählst du $4$ Schichten mit jeweils $48$ Einheitswürfel. Insgesamt passen somit $4 \cdot 48 = 192$ Einheitswürfel in den Quader.
  Die Antwort " $192$ Einheitswürfel" ist also richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

In der Tabelle wurden die Maße verschiedener Quader angegeben. Die Volumina sind zunächst unbekannt und sollen in dieser Aufgabe berechnet werden.

Länge	Breite	Höhe	Volumen
$10\;\text{cm}$	$5\;\text{cm}$	$4\;\text{cm}$	$V_1$
$2\;\text{m}$	$0{,}5\;\text{m}$	$0{,}5\;\text{m}$	$V_2$
$2\;\text{dm}$	$15\;\text{cm}$	$100\;\text{mm}$	$V_3$
$0{,}01\;\text{m}$	$10\;\text{mm}$	$0{,}1\;\text{dm}$	$V_4$

9
Die großen Flächen eines Zauberwürfels bestehen aus $9$ kleinen bunten Flächen. Insgesamt hat der Würfel einen Oberflächeninhalt von $900\,\mathrm{cm}^2$ .
Wie groß sind die Flächen der einzelnen Farbquadrate?
cm²

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Quadrats
Um die Fläche eines einzelnen Farbquadrates zu bestimmen, kannst du zuerst den gegebenen Gesamtflächeninhalt des Zauberwürfels von $900\,\mathrm{cm}^2$ durch sechs teilen, damit du den Flächeninhalt von einer der sechs großen Flächen des Zauberwürfels erhältst.
$A_\text{große Fläche}$
$=A_\mathrm{gesamt}:6$
$=900\,\mathrm{cm}^2:6$
$=150\,\mathrm{cm}^2$
Berechnung des Flächeninhaltes von einem einzelnen Farbquadrat
Da sich eine große Fläche aus neun einzelnen Farbquadraten zusammensetzt, kannst du den gerade eben ausgerechneten Flächeninhalt der großen Fläche durch neun teilen, um den Flächeninhalt eines einzelnen Farbquadrates zu bestimmen.
$A_\text{einzelnes Farbquadrat}$
$=A_\text{große Fläche}:9$
$=150\,\mathrm{cm}^2:9$
$=16{,}\overline{6}\,\mathrm{cm}^2$
$\approx16{,}7\,\mathrm{cm}^2$
Antwort:
Die Fläche eines einzelnen Farbquadrates $A_\text{einzelnes Farbquadrat}$ ist ca. $16{,}7\,\mathrm{cm}^2$ groß.
10
Gegeben ist ein Würfel mit der Oberfläche $O=24\,\mathrm{cm}^2$ .
Berechne das Volumen $V$ des Würfels.
cm³

Für diese Aufgabe benötigst Du folgendes Grundwissen: Oberfläche und Volumen eines Würfels
$a$ bezeichnet die Seitenlänge des Würfels.
$\def\arraystretch{1.25} \begin{array}{l}O=a^2\cdot6\\V=a^3\end{array}$
Berechne zunächst die Seitenlänge des Würfels.
$a^2\cdot6=24\,\mathrm{cm}^2 \quad | :6$
$a^2=4\,\mathrm{cm}^2$
ziehe die Wurzel
$a=2\,\mathrm{cm}$
Berechne nun das Volumen des Würfels.
$V=(2\,\mathrm{cm})^3=8\,\mathrm{cm}^3.$
Das Volumen des Würfels beträgt $8\,\mathrm{cm}^3$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle V_{\mathrm{Quader}}$	$=$	$\displaystyle l\cdot b\cdot h$
	↓	Setze die Werte ein
	$=$	$\displaystyle 0{,}8\,\mathrm m\cdot0{,}45\,\mathrm m\cdot1{,}5\,\mathrm m$
	↓	Multipliziere
	$=$	$\displaystyle 0{,}54\,\mathrm m^3$
	↓	Rechne $\mathrm m^3$ in $\mathrm{dm}^3$ um
	$=$	$\displaystyle 540\,\mathrm{dm}^3$
	↓	Rechne $\mathrm{dm}^3$ in Liter um
	$=$	$\displaystyle 540 \,\mathrm l$

$\displaystyle 1\,\mathrm m-12\cdot x$	$=$	$\displaystyle 0{,}04\,\mathrm m$	$\displaystyle +(12x-0{,}04\,\mathrm m)$
$\displaystyle 0{,}96\,\mathrm m$	$=$	$\displaystyle 12x$	$\displaystyle \div 12$
$\displaystyle x$	$=$	$\displaystyle 0{,}08\,\mathrm m=8\,\mathrm{cm}$

Aufgaben zu Oberfläche und Volumen von Würfel und Quader

Vorüberlegungen

Schätzen der Maße

Berechnung durch Angabe

Berechnung des Volumens

Anwendungen

Oberflächeninhalt

Oberfläche des Quaders

Oberfläche des Würfels

Vergleich

Hast du eine Frage oder Feedback?

Volumen

Volumen des Quaders

Volumen des Würfels

Erkenntnis

Hast du eine Frage oder Feedback?

Anzahl der Würfel in einer Reihe

Anzahl der Würfel in einer Schicht

Anzahl der Würfel im Paket

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechnung des Flächeninhaltes von einem einzelnen Farbquadrat

Antwort: