1 Übersicht
Ziel dieses Kurses ist es, das Konzept der Vielfachheit einer Nullstelle einzuführen und dessen Beziehung zum Graphen einer Polynomfunktion zu erläutern.
Inhalte
Nullstellen und Vorzeichenwechsel
Definition der Vielfachheit einer Nullstelle
Doppelte und dreifache Nullstellen
Gerade und ungerade Vielfachheiten
Skizzieren des Graphen mithilfe von Vielfachheiten
Vorwissen
Definition der Nullstelle
Linearfaktordarstellung einer Polynomfunktion
Berechnung von Nullstellen bei Polynomfunktionen
Charakteristischer Verlauf einer Polynomfunktion bzw. Grenzwerte im Unendlichen
Die genannten Inhalte werden auch im Kurs Berechnungsmethoden - Nullstellen von Polynomfunktionen behandelt. Dieser eignet sich gut, um die obigen Begriffe zu wiederholen.
2 Vielfachheit einer Nullstelle (1|8)
Die Nullstellen einer Funktion können eine große Hilfe sein, den Graphen der Funktion zu zeichnen. Oft reichen diese allein aber nicht aus. Schau dir dazu die unteren drei Graphen und an.
Dir fällt bestimmt auf, dass alle drei den charakteristischen Verlauf "von links oben nach rechts oben" haben. Weiterhin haben alle dieselben Nullstellen, nämlich .
Graph
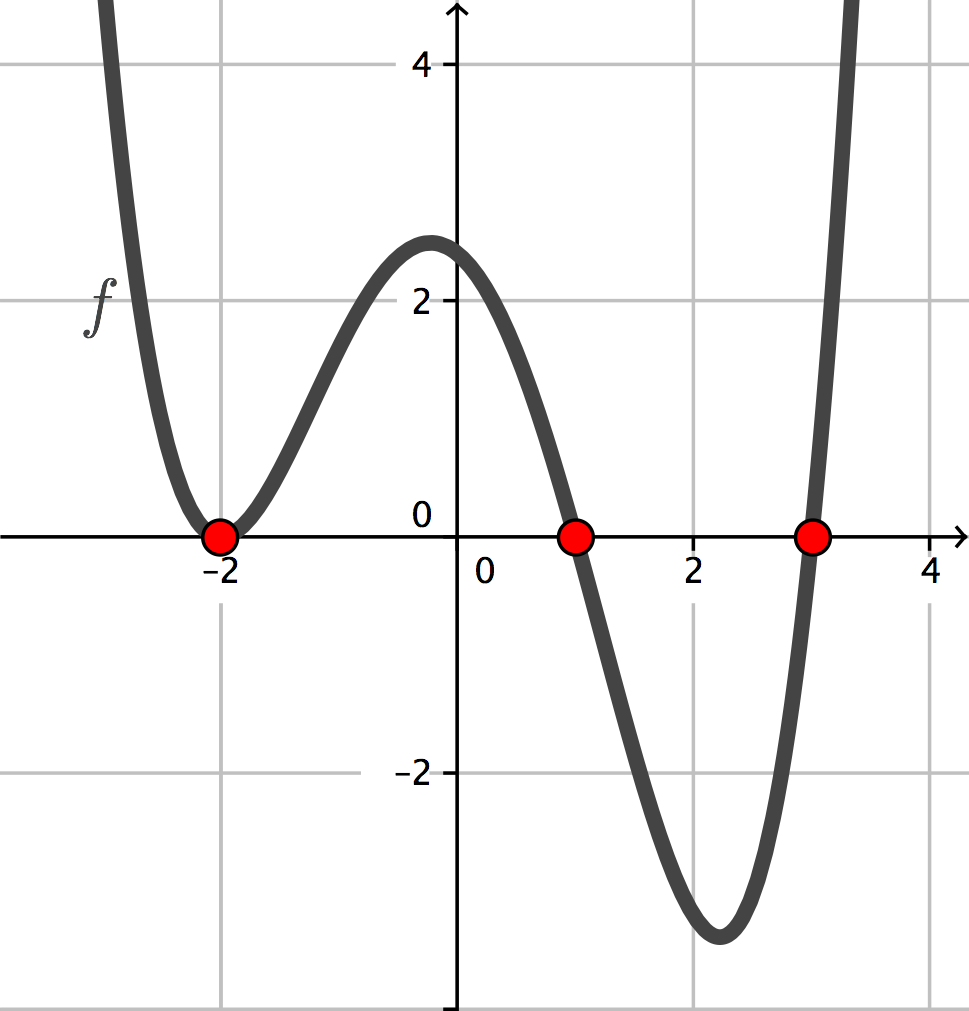
Graph
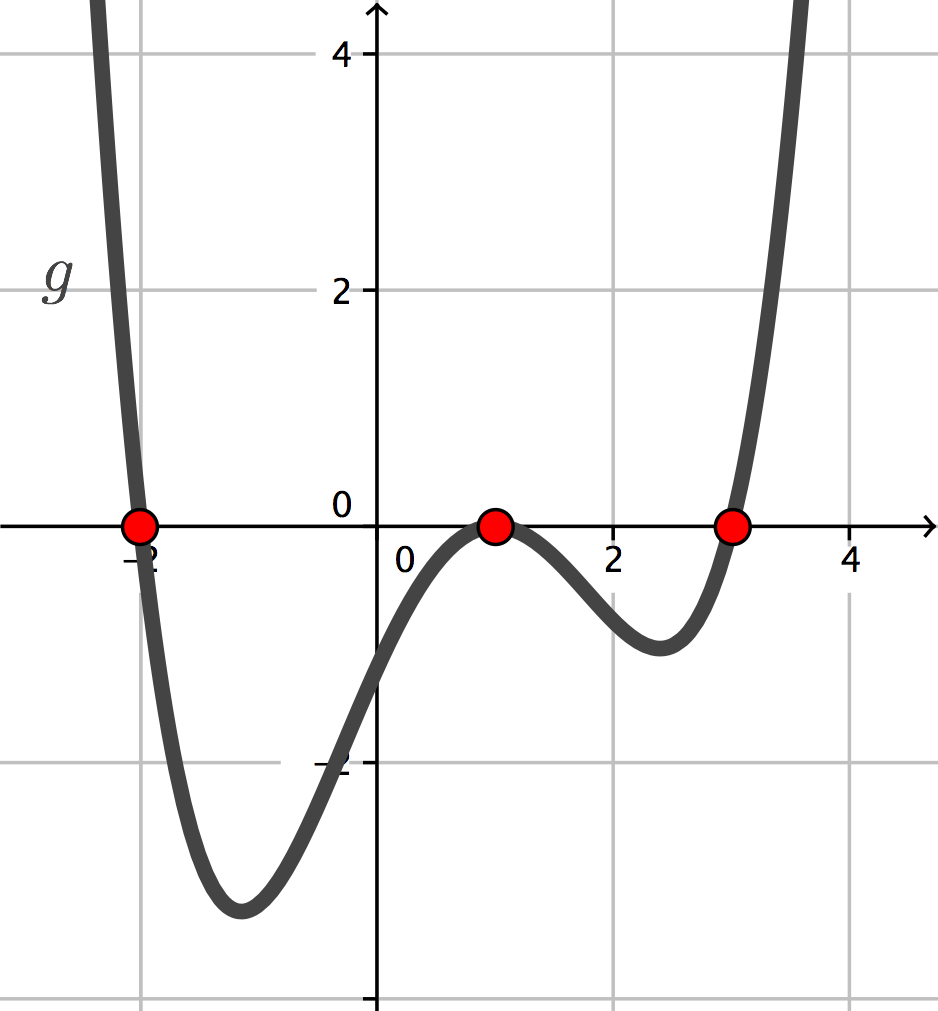
Graph
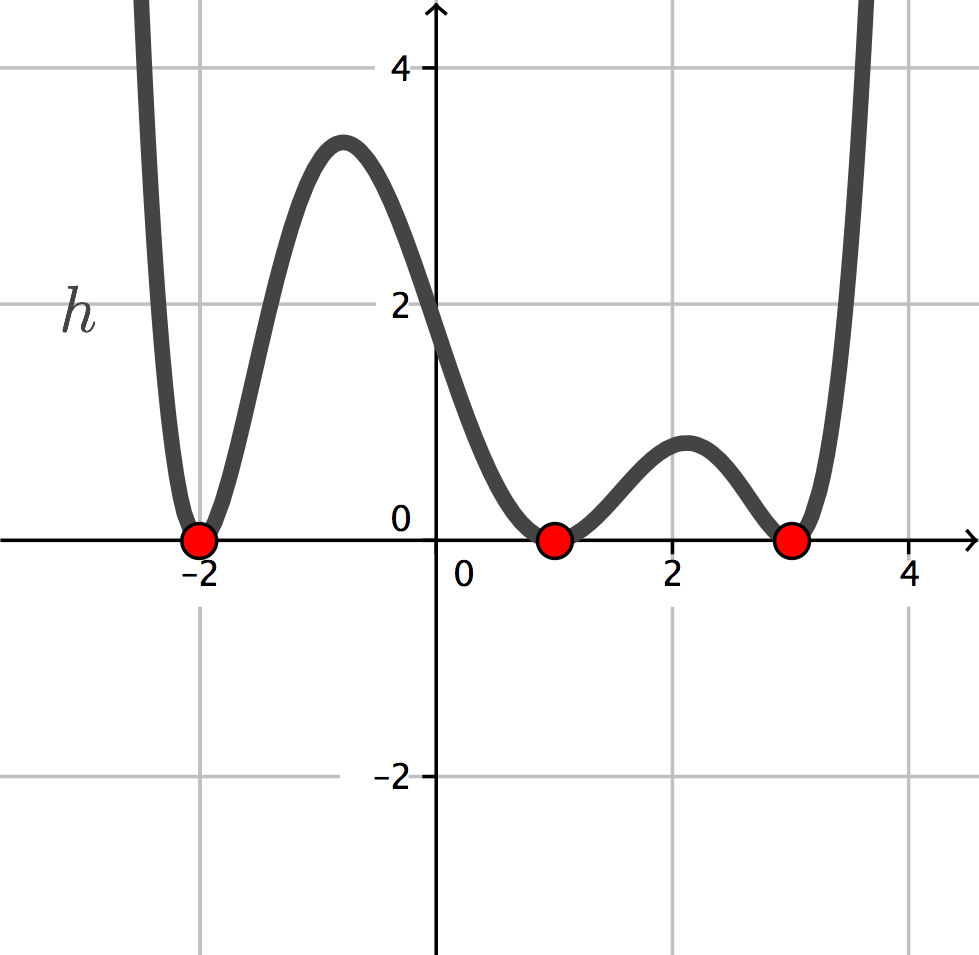
Trotzdem sehen die Graphen alle sehr verschieden aus. Es reicht offensichtlich nicht aus, den charakteristischen Verlauf des Graphen und die Nullstellen zu kennen, um den Graphen einer Polynomfunktion bestimmen zu können.
An den Nullstellen unterscheiden sich die Graphen darin, ob und wie sie das Vorzeichen wechseln. An manchen Nullstellen wird die -Achse überquert (z.B. bei und ) und an anderen wird die -Achse nur berührt (z.B. bei und ).
Wir unterscheiden also zwischen:
Nullstellen mit Vorzeichenwechsel (VZW), bei denen der Graph die -Achse überquert und
Nullstellen ohne Vorzeichenwechsel (kein VZW), bei denen die -Achse nur berührt wird.
Schaue dir die drei Graphen noch einmal an und überlege, welche Nullstellen von und einen VZW haben. Klappe dann die unteren Felder auf.
3 Vielfachheit einer Nullstelle (2|8)
Damit wir am Funktionsterm feststellen können, ob der Graph an den Nullstellen die -Achse überquert (VZW) oder nur berührt (kein VZW), brauchen wir den Begriff des Linearfaktors.
Du hattest schon festgestellt, dass die Graphen von und die gleichen Nullstellen haben. Ihre Linearfaktordarstellungen werden also sehr ähnlich sein.
Hier findest du wieder die Graphen von und . Darunter sind die dazugehörigen Funktionsterme und in Linearfaktordarstellung angezeigt.
Vergleiche die Linearfaktoren und in den verschiedenen Funktionsvorschriften. Was fällt dir auf?

Graph
=

Graph
=

Graph
Manche Linearfaktoren kommen in den Funktionstermen mehrmals vor, bzw. sind sie als Potenz (mit Exponent ) geschrieben.
Schauen wir uns den Funktionsterm etwas genauer an:
=
Zur Nullstelle gehört der Linearfaktor . Dieser kommt nur einmal in vor. Weiterhin überquert bei die -Achse.
Zur Nullstelle gehört der Linearfaktor . Dieser kommt zweimal in vor (bzw. hat den Exponenten ). Bei berührt nur die -Achse.

Graph
Vergleiche jetzt nochmal die Linearfaktoren in den Funktionstermen mit dem Verhalten des Graphen an den Nullstellen.
4 Vielfachheit einer Nullstelle (3|8)
Um die Frage zu klären, was bei Nullstellen passiert, bei denen die zugehörigen Linearfaktoren mehrfach vorkommen, führen wir jetzt einen neuen Begriff ein - die Vielfachheit.
Bei Polynomfunktionen unterscheidet man Nullstellen nach ihren Vielfachheiten.
Die Vielfachheit einer Nullstelle gibt an, wie oft diese in einer Funktion vorkommt. Genauer, wie oft ihr zugehöriger Linearfaktor bei der Linearfaktordarstellung der Polynomfunktion vorkommt.
Ist die Vielfachheit einer Nullstelle gleich eins, so nennt man diese Nullstelle einfach. Nullstellen mit einer Vielfachheit größer als heißen mehrfache Nullstellen.
Betrachte zum Beispiel die Funktion . hat eine zweifache (man sagt auch doppelte) Nullstelle bei .
Man sagt auch:
ist eine Nullstelle zweiter Ordnung.
Die Nullstelle hat Vielfachheit .
Die Nullstelle hat Ordnung .
Dabei sind alle diese Formulierungen gleichbedeutend.
5 Vielfachheit einer Nullstelle (4|8)
Beispiel
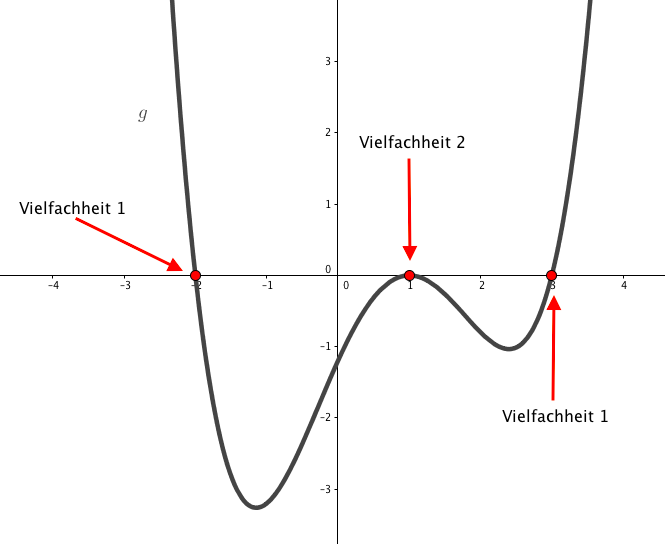
Schauen wir uns doch die Funktion unter dem Aspekt der Vielfachheit an.
Die Funktion ist bereits in Linearfaktoren zerlegt. Dort kommt der Faktor genau zweimal vor, denn .
Die Faktoren und kommen beide genau einmal vor. Ihre Nullstellen haben also jeweils die Vielfachheiten und .
6 Vielfachheit einer Nullstelle (5|8)
Hier noch ein Video zu doppelten und dreifachen Nullstellen. Viel Spaß!
Laden
7 Aufgaben zur Vielfachheit einer Nullstelle
Bestimme die Vielfachheiten der Nullstelle(n) zu folgenden Funktionen
Laden
Laden
Laden
Laden
8 Vielfachheit einer Nullstelle (6|8)
Auf den ersten Seiten dieses Kurses, haben wir beobachtet, dass bei Nullstellen mit Vielfachheit der Graph die -Achse überquert, und bei Nullstellen mit Vielfachheit der Graph die Achse nur berührt.
Was passiert nun bei Nullstellen höherer Ordnung (bzw. mit höherer Vielfachheit)?
Benutze das Applet auf dieser Seite, um diese Fragestellung zu untersuchen:
9 Vielfachheit einer Nullstelle (7|8)
Wie du dir vielleicht schon denken konntest, gilt:
An Nullstellen, mit ungerader Vielfachheit (), ergibt sich ein Vorzeichenwechsel. Der Funktionsgraph überquert an dieser Nullstelle die -Achse.
An Nullstellen, mit gerader Vielfachheit (), ergibt sich kein Vorzeichenwechsel. Der Funktionsgraph bleibt also auf einer Seite der -Achse und berührt diese nur.
10 Vielfachheit einer Nullstelle (8|8)
Auf dieser Kursseite werden wir nun versuchen, mithilfe von Nullstellen und deren Vielfachheiten, den Graphen einer Polynomfunktion zu skizzieren.
Wir betrachten dazu:
Schritt - Nullstellen und deren Vielfachheiten bestimmen
Da schon in Linearfaktordarstellung ist, kann man die Nullstellen und deren Vielfachheiten einfach ablesen. Bei uns ergibt sich eine…
einfache Nullstelle bei
doppelte Nullstelle bei (durch das )
einfache Nullstelle bei
einfache Nullstelle bei .
Schritt - Charakteristischen Verlauf bestimmen
Zuerst bestimmen wir den charakteristischen Verlauf der Polynomfunktion, also das Verhalten im Unendlichen.
Hier nochmal der Funktionsterm:
Es handelt sich hier um eine Polynomfunktion vom Grad , denn der Funktionsterm besteht aus dem Term und drei Faktoren (jeweils vom Grad ): .
Weiterhin ist der Koeffizient vor den Faktoren negativ.
Der charakteristische Verlauf ist also gleich dem Verlauf einer Potenzfunktion mit ungeradem Grad und negativem Vorzeichen. Daher ergibt sich der Verlauf "von links oben nach rechts unten".
Zeichne nun alle Nullstellen ein.
Wir wissen, dass der Graph von im Negativen von kommt ("links oben"). Dies wird rechts in der Skizze durch den blauen Strich angedeutet.
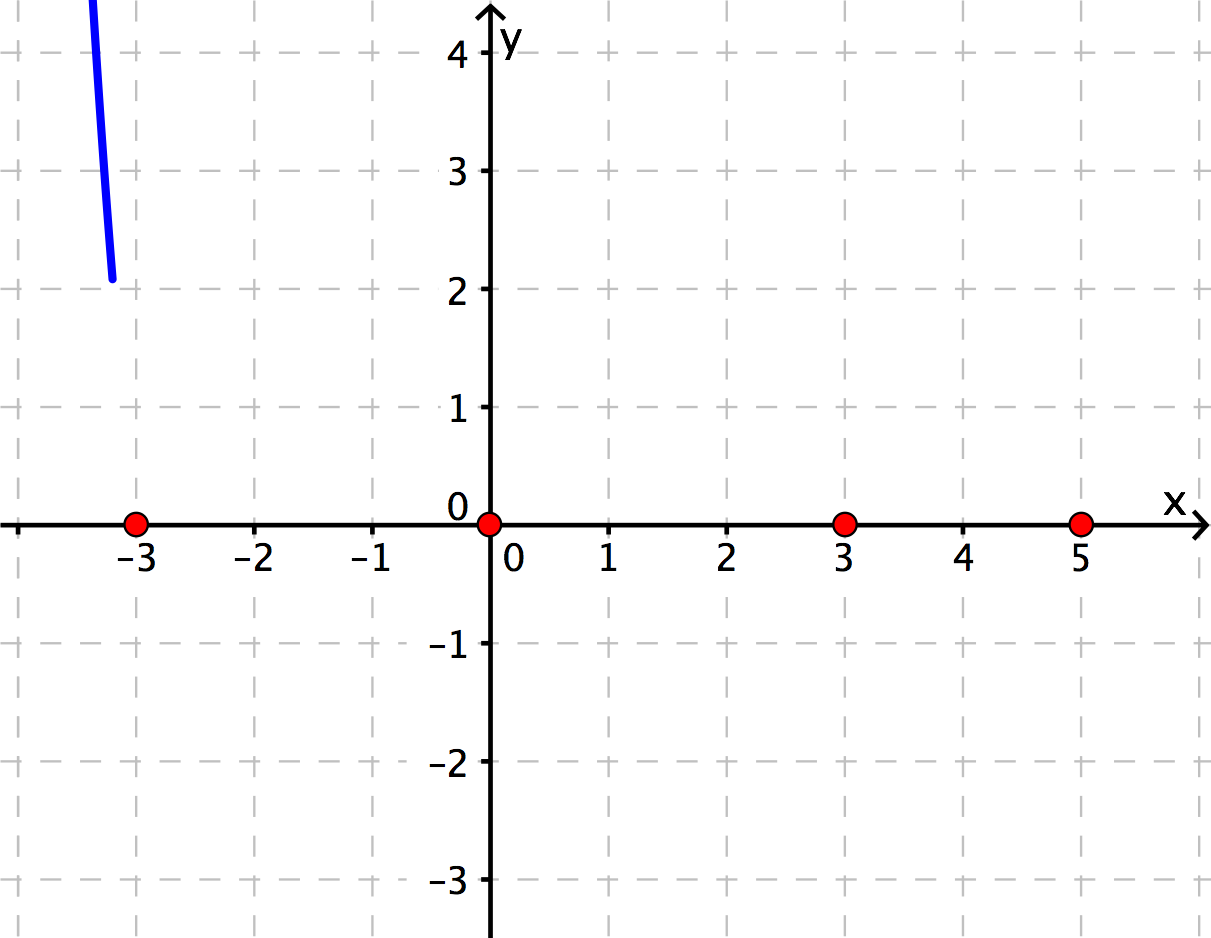
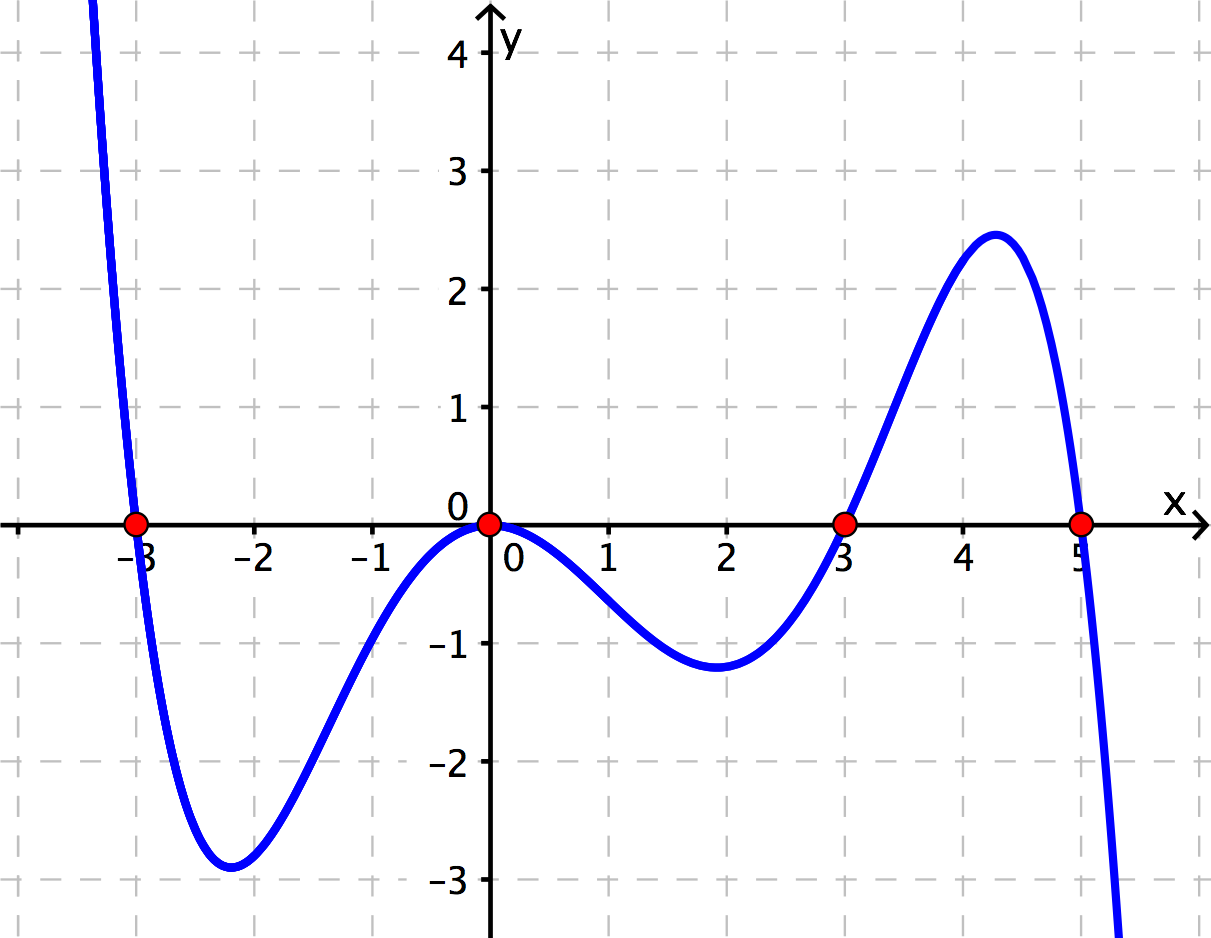
Schritt 3 - Graph mithilfe der Vielfachheiten skizzieren
. Nullstelle
Bei haben wir eine einfache Nullstelle. Es ergibt sich also ein VZW der Funktionswerte. Der Graph überquert die -Achse und gelangt in den negativen -Bereich.
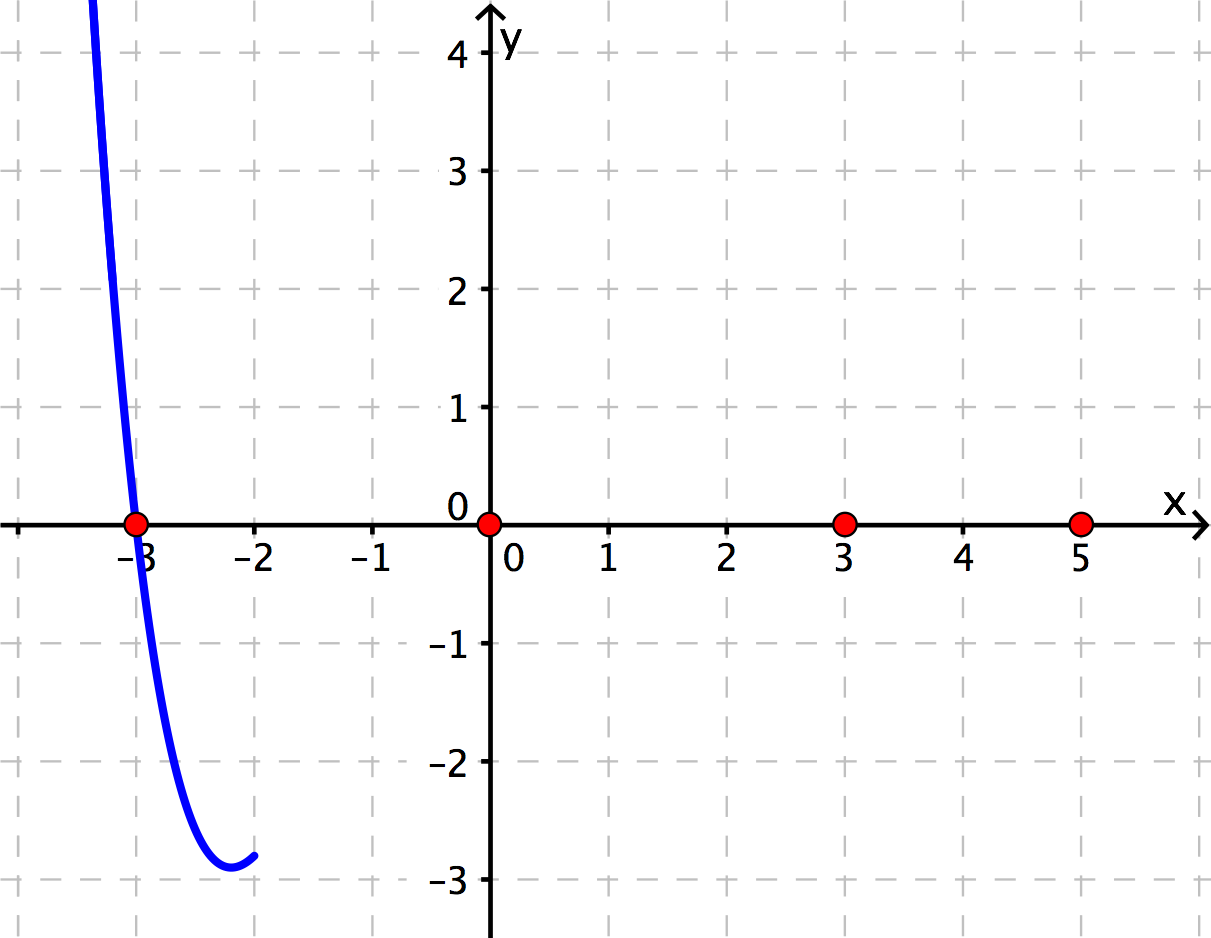
. Nullstelle
Der Graph kehrt nun zur -Achse zurück. Da wir bei eine doppelte Nullstelle vorfinden, wechselt die Funktion nicht das Vorzeichen und bleibt im negativen -Bereich. Der Graph berührt also nur die -Achse.
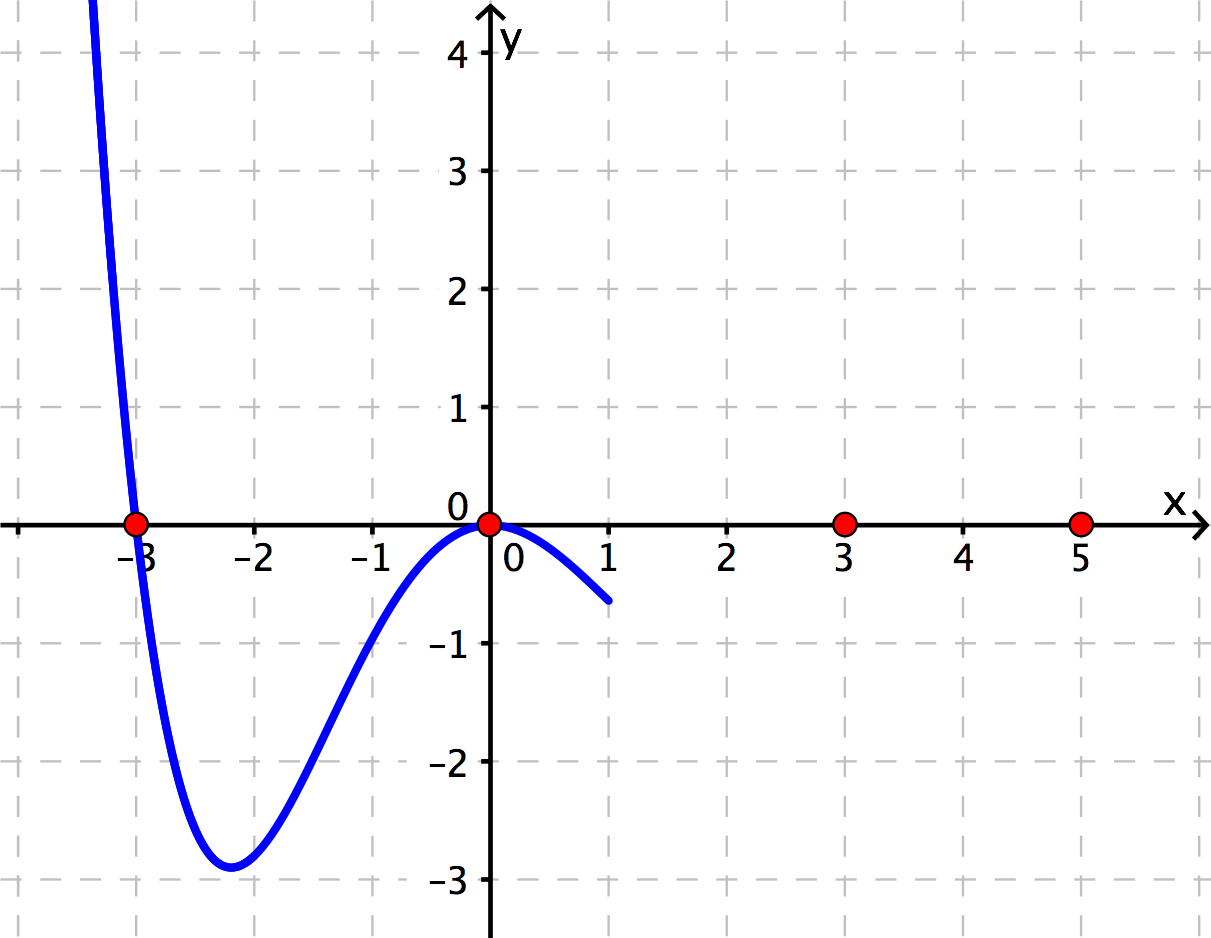
. Nullstelle
Bei gibt es eine einfache Nullstelle. Daher überquert der Graph die -Achse und gelangt in den positiven -Bereich.
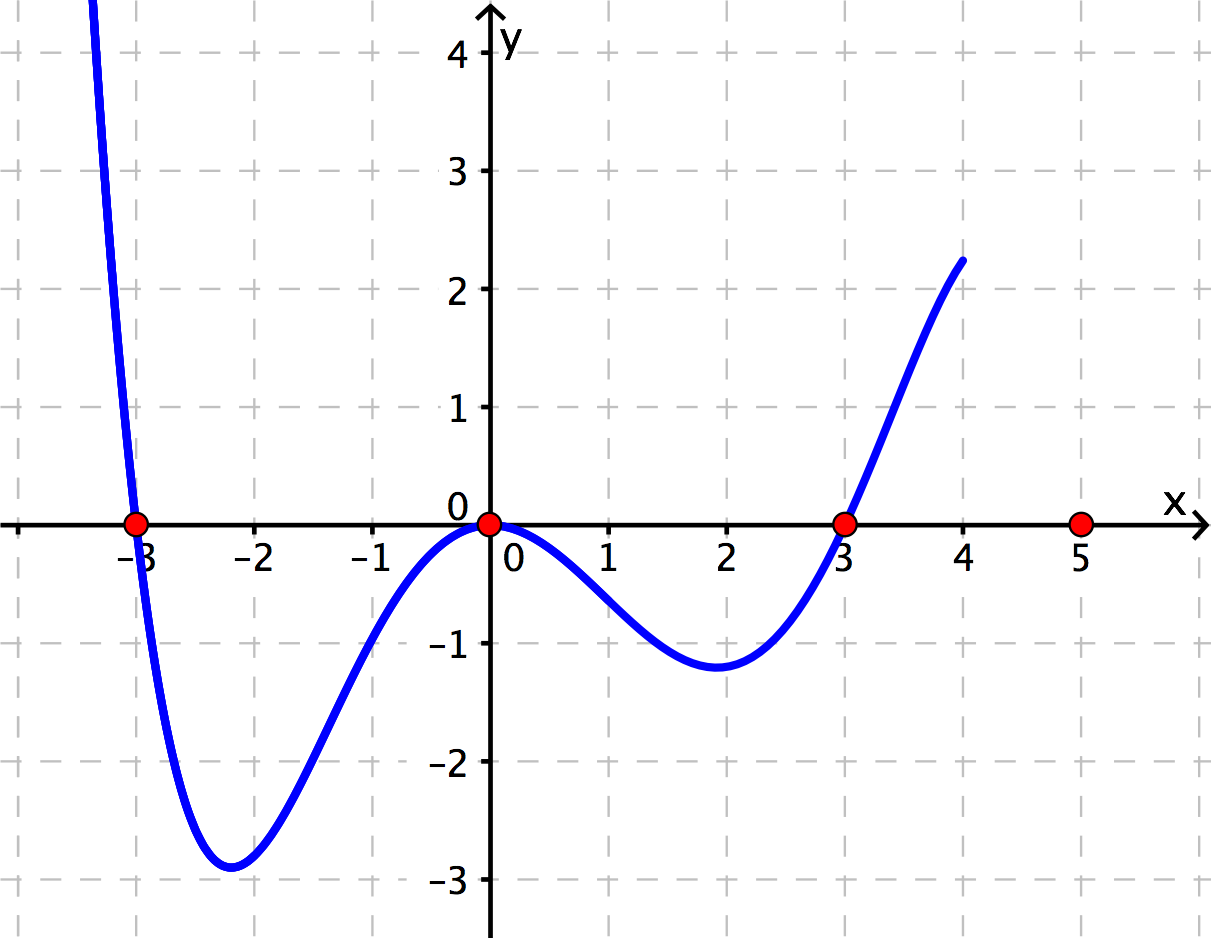
. Nullstelle
Die letzte Nullstelle ist bei und hat auch Ordnung . Daher findet wieder ein Vorzeichenwechsel statt und der Graph überquert die -Achse.
Es gibt keine weiteren Nullstellen. Der Graph bleibt daher im negativen -Bereich. Dies entspricht auch den Vorgaben des charakteristischen Verlaufs ("links oben nach rechts unten").
11 Aufgaben zur Vielfachheit einer Nullstelle 2
Hier findest du weitere Aufgaben:
Aufgabe
Laden
Aufgabe
Laden
Aufgabe
Laden
12 Zusammenfassung
Was nehmen wir also aus diesem Kurs mit?
Die Vielfachheit einer Nullstelle gibt an, wie oft diese in einer Funktion vorkommt. Genauer, wie oft ihr zugehöriger Linearfaktor bei der Linearfaktordarstellung der Polynomfunktion vorkommt.
Bei Nullstellen, mit ungerader Vielfachheit, wechselt der Funktionsgraph das Vorzeichen. Bei Nullstellen, mit gerader Vielfachheit, wechselt der Funktionsgraph das Vorzeichen nicht.
Für den unüberzeugten Schüler…
Das Applet auf den vorherigen Kursseiten veranschaulicht unsere Regel mit dem Vorzeichenwechsel und den Vielfachheiten der Nullstellen. Wir haben dann behauptet, dass dies immer der Fall ist. Doch warum genau ist das so?
Wenn dir das Applet nicht reicht, um dieser Regel blind zu vertrauen und du eine rechnerische Erklärung sehen willst, gehe auf die nächste Kursseite.
Feedback
Damit wir unseren Kurs für die Zukunft verbessern können, würden wir uns sehr über ein Feedback von dir freuen. Es dauert auch nur 3 Minuten!
Klicke dazu auf diesen Link.
13 Rechnerische Erklärung (für den unüberzeugten Schüler)
Du willst wissen, warum bei gerader Vielfachheit einer Nullstelle kein Vorzeichenwechsel passiert, während bei ungerader Vielfachheit schon? Dann bist du hier genau richtig!
Wir erklären diese Regel rechnerisch an der Funktionsvorschrift von . Diese Rechnungen lassen sich genau so bei jeder beliebigen Polynomfunktion durchführen.
Die Vorschrift der Funktion lautet:
Wir wissen bereits, dass einfache und doppelte Nullstellen hat. Hier nochmal der Graph von .

Gilt diese Regel auch für Nullstellen mit anderen Vielfachheiten? Überlege es für einen Moment.
