Aufgaben zu Flächen von Dreiecken und Vierecken

1
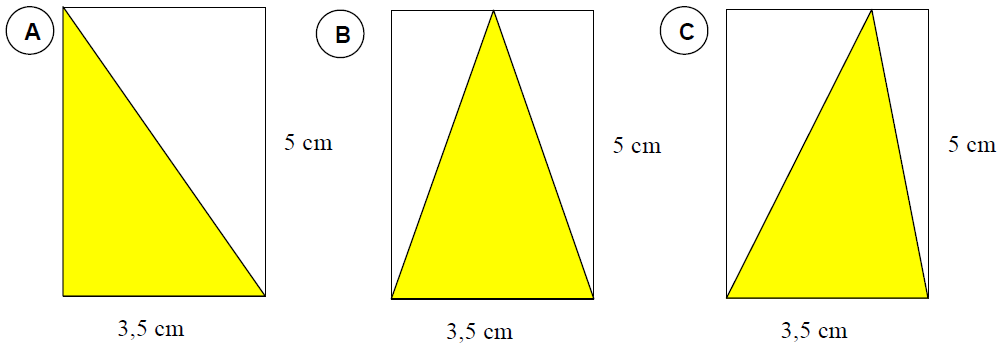
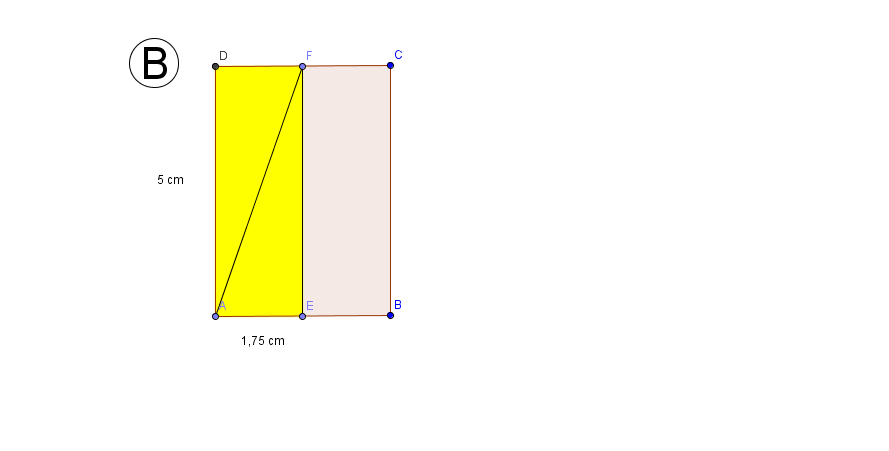
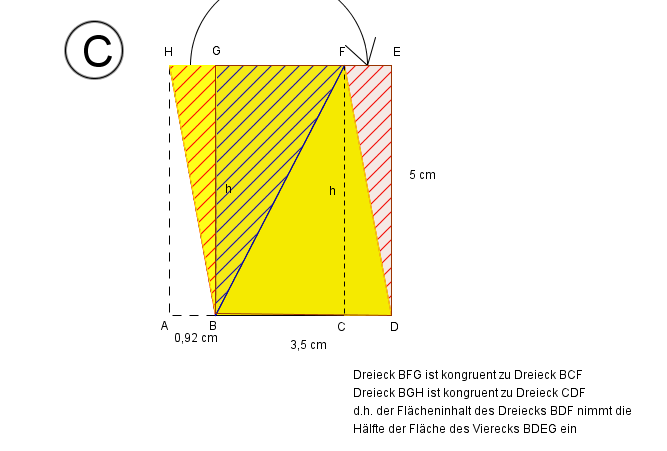
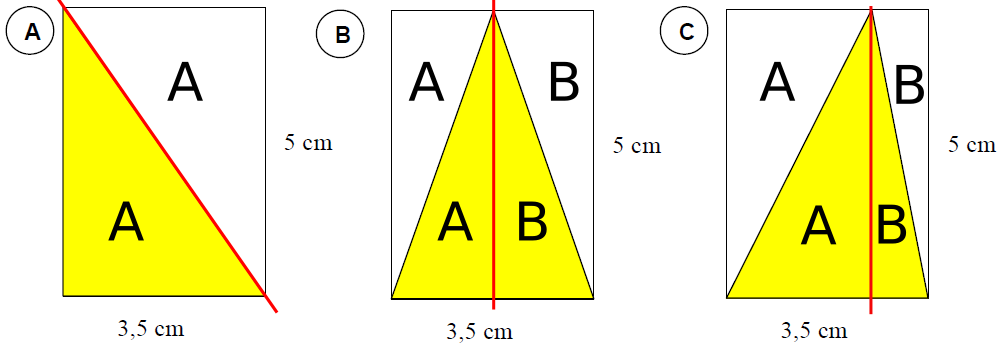
In Bild A sieht man sofort, dass der Flächeninhalt des gelben Dreiecks halb so groß ist wie der des umgebenden Rechtecks. Gilt dies auch für die Bilder B und C? Begründe deine Antwort mit Hilfe geeigneter Skizzen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalte
Das Dreieck B wird durch die Mitte in zwei geteilt. Das Dreieck AEF nimmt genau soviel Platz ein wie das Dreieck ADF, da es die Hälfte vom Dreieck AEF ist. Setzt man beide Dreiecke nun in eine Hälfte des Vierecks, ist das Viereck zur Hälfte gefüllt.
Wenn du das Rechteck an der richtigen Stelle unterteilst, siehst du sofort, dass jeweils ein gelbes und weißes Dreieck deckungsgleich (kongruent) ist.
Da die Grundseite $g$ und die Höhe $h$ immer gleich bleiben, bleibt auch der Flächeninhalt des Dreiecks immer gleich. Egal wo die Spitze des Dreiecks ist, der Flächeninhalt ist immer die Hälfte des Rechtecks.
Um die Aufgabe zu lösen, hilft es sehr, sich das Dreieck vorzustellen oder eine Skizze anzufertigen. Es ist dann möglich zu sehen wie die Dreiecke umgebaut werden können. Wenn es einem nicht direkt auffällt, kann man - falls Zahlen angegeben sind - den Flächeninhalt ausrechnen und somit eine klare Lösung erhalten.
2
Berechne für ein Rechteck die fehlenden Größen:

Länge l
Breite b
Flächeninhalt A
Umfang U
a)
5 cm
7 dm
b)
30 cm
1,4 m
c)
120 m
6 ha
d)
80 cm
4 m²

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Rechteck
Länge l
Breite b
Flächeninhalt A
Umfang U
a)
5 cm
7 dm
3,5 dm²
15dm
b)
30 cm
0,4 m
0,12 m²
1,4 m
c)
500 m
120 m
6 ha
1240 m
d)
80 cm
5 m
4 m²
11,6 m
a) Berechnung Flächeninhalt A und Umfang U
Gegeben:
Länge l = 5cm Breite b = 7dm
Gesucht: Flächeninhalt A und Umfang U
Die Länge l musst du erst in die Einheit dm umrechnen. Die Länge l wird mit der Breite b multipliziert um den Flächeninhalt A zu erhalten. Die Werte werden für l und b eingesetzt, um das Ergebnis von U zu erhalten.
$A = 0,5 d m \cdot 7 d m = 3,5 d m^{2}$
$U = 2 l + 2 b$
$U = 2 \cdot 0,5 d m + 2 \cdot 7 d m = 15 d m$
b) Berechnung Breite b und Flächeninhalt A
Gegeben:
Länge l = 30cm Umfang U = 1,4m
Gesucht: Breite b und Flächeninhalt A
Die Länge l wird in Meter umgerechnet und der Anteil am Umfang U abgezogen
Die Breite b bekommst du aus dem Umfang U, indem die Länge l abgezogen wird und die Breite b durch Teilen (Division) hervorgeht.
Um von 2b (2 mal b) den Wert für b herauszubekommen, teilst du das Ergebnis durch 2.
Durch die erhaltene Breite b kannst du dann den Flächeninhalt A ausrechnen.
$U = 2 l + 2 b$
$U - 2 l = 1,4 m - 2 \cdot 0,3 m = 0,8 m$
$2 b = 0,8 m$
$b = 0,8 m : 2 = 0,4 m$
$A = l \cdot b$
$A = 0,3 m \cdot 0,4 m = 0,12 m^{2}$
c) Berechnung Länge l und des Umfang U
Gegeben:
Breite b = 120m Flächeninhalt A = 6ha
Gesucht: Länge l und Umfang U
Der Flächeninhalt A wird in m² umgerechnet und durch die Breite b geteilt. Um die Länge l zu erhalten, teilst du den Flächeninhalt A durch die Breite b.
Als Ergebnis kommt der andere Teil vom Flächeninhalt, die Länge l als Ergebnis heraus.
$A = l \cdot b$
$A = 60000 m^{2} : 120 m = 500 m$
$l = 500 m$
Die Werte der Länge l und der erhaltenen Breite b werden eingesetzt, das Ergebnis ist der Umfang.
$U = 2 l + 2 b$
$U = 2 \cdot 500 m + 2 \cdot 120 m = 1240 m$
d) Berechnung Breite b und Umfang U
Gegeben:
Länge l = 80cm Flächeninhalt A = 4m²
Gesucht: Breite b und Umfang U
Die Länge l rechnest du in Metern um, damit der Flächeninhalt durch l geteilt wird.
Durch Teilen vom Flächeninhalt durch die vorhandene Länge l bekommst du das Ergebnis der Breite b.
$A = l \cdot b$
$A = 4 m^{2} : 0,8 m = 5 m$
$l = 5 m$
Für den Umfang müssen die Länge l und die ausgerechnete Breite b eingesetzt werden
$U = 2 l + 2 b$
$U = 2 \cdot 5 m + 2 \cdot 0,8 m = 9,6 m$
3
Wie lang muss ein Zaun sein, der ein quadratisches Grundstück der Fläche $6 a 25 m^{2}$ umgibt?
m

Für diese Aufgabe benötigst Du folgendes Grundwissen: Viereck
Seitenlänge des Grundstücks
$6 a 25 m^{2}$
6 Ar umrechnen in Quadratmeter und die gegebene Fläche in die Flächenformel des Quadrats einsetzen.
$x^{2} = 625 m^{2}$
Überlege: Welche Zahl im Quadrat ergibt 625?
$x = 25 m$
Umfang des Grundstücks
$x = 25 m$
Nimm die Seite des Quadrats mal 4 um den Umfang zu berechnen.
$U = 4 \cdot 25 m = 100 m$
$\Rightarrow$ Der Zaun muss $100 m$ lang sein.
4
Verlängert man zwei gegenüberliegende Seiten eines Quadrats um jeweils 3 cm und verkürzt die anderen Seiten um jeweils 2 cm, so entsteht ein Rechteck, dessen Flächeninhalt um $1 {cm}^{2}$ größer ist als der des Quadrats. Wie lang sind die Seiten des Quadrats?
cm

Für diese Aufgabe benötigst Du folgendes Grundwissen: Aufstellen und Lösen von Gleichungen
Variable einführen
a = Seite des Quadrats
Gleichung aufstellen
Drücke die Angaben mithilfe von a aus:
$a$ : Seite des Quadrats
$a + 3$ : lange Seite des Rechtecks
$a - 2$ : kurze Seite des Rechtecks
$a^{2} + 1$ : Flächeninhalt des Rechtecks in Abhängigkeit vom Quadrat
$(a + 3) (a - 2)$ : Flächeninhalt in Abhängigkeit von den Rechteckseiten
Gleichung aufstellen:
"Quadrat + 1 = Rechteckfläche (Länge mal Breite)"
$a^{2} + 1 = (a + 3) (a - 2)$
Gleichung lösen
Gleichung umformen und Klammern ausmultiplizieren .
$a^{2} + 1 = a^{2} - 2 a + 3 a - 6 | - a^{2}$
$1 = a - 6 | + 6$
$7 = a$
Lösung überprüfen:
Wenn die Quadratseite $7 c m$ ist, dann wäre die Fläche des Quadrats $a^{2} = 49 c m^{2}$ und die Fläche vom Rechteck: $10 c m \cdot 5 c m = 50 c m^{2}$ und damit $1 c m^{2}$ größer als die Fläche des Quadrats.
Die Lösung stimmt also!
Antwortsatz
$\Rightarrow$ Die Länge der Seite a des Quadrats beträgt 7cm.
5
Ein rechteckiges Grundstück ist 21m lang und hat einen Flächeninhalt von $14 a 70 m^{2}$ . Berechne die Breite und den Umfang des Grundstücks.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Rechteck
Gegeben: Länge $l = 21 m$ Flächeninhalt $A = 14 a 70 m^{2}$
Gesucht: Breite $b$ und Umfang $U$
Rechne den gegebenen Flächeninhalt in die Einheit $m^{2}$ um.
$14 a 70 m^{2}$ $=$ $1400 m^{2} + 70 m^{2} = 1470 m^{2}$
↓
Berechne die Breite $b$ mit Hilfe der Formel für den Flächeninhalt.
$A$ $=$ $l \cdot b$
↓
Setze die gegebenen Zahlenwerte für $l$ und $A$ ein.
$1470 m^{2}$ $=$ $21 m \cdot b$
↓
Löse die Gleichung nach $b$ auf.
$b$ $=$ $\frac{1470 m^{2}}{21 m} = 70 m$
↓
Berechne mit diesem Ergebnis den Umfang.
$U$ $=$ $2 b + 2 l$
↓
Setze die Zahlenwerte ein.
$U$ $=$ $2 \cdot 70 m + 2 \cdot 21 m$
$U$ $=$ $182 m$
Das Rechteck hat eine Breite von 70 m und einen Umfang von 182 m.
6
Manuelas Zimmer ist 4 m lang, 3,5 m breit und 2,5 m hoch.
Eine der beiden großen Wandflächen soll einen gelben Farbanstrich erhalten. Von einem Farbtopf mit der Aufschrift "Inhalt 2,5 l ausreichend für 20 $m^{2}$ - 25 $m^{2}$ " ist noch die Hälfte übrig.
Reicht die Menge für den Anstrich der Wand? Begründe deine Antwort durch Rechnung.
Ja, die Menge reicht noch für den Anstrich.
Nein, die Menge reicht nicht mehr für den Anstrich.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Rechteck
Die "große" Wandfläche ist 4 m lang und 2,5 m hoch. Berechne die rechteckige Fläche der Wand.
$4 m \cdot 2,5 m = 10 m^{2}$
Überlege dir für wie viel $m^{2}$ Wandfläche die restliche Farbe noch reicht. Es ist noch die Hälfte der Farbe da.
Die Farbe reicht für
$\frac{1}{2} \cdot 20 m^{2} = 10 m^{2}$
bis
$\frac{1}{2} \cdot 25 m^{2} = 12,5 m^{2}$ .
Vergleiche das Ergebnis mit der erechneten Wandfläche.
Die Farbe im Topf reicht also aus.
7
Ein rechteckiger Garten der Länge 12m und der Breite 9,5m soll eingezäunt werden. Wie lang ist der Zaun, wenn für zwei Gartentore jeweils 2,7m ausgespart werden?
m

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnung am Rechtek
Länge $l = 12 m$
Breite $b = 9,5 m$
Die Zaunlänge entspricht dem Umfang eines Rechtecks. Berechne also den Umfang $U$ .
$U = 2 l + 2 b$
Setzte die gegebenen Zahlenwerte für $l$ und $b$ ein.
$U = 2 \cdot 12 m + 2 \cdot 9,5 m$
$U = 43 m$
Für zwei Gartentore sollen jeweils 2,7 m ausgespart werden. Subtrahiere also die Gesamtlänge der Gartentore von dem Umfang des Gartens.
$2 \cdot 2,7 m = 5,4 m$
$43 m - 5,4 m = 37,6 m$
Der Zaun ist $37,6 m$ lang.

	Länge l	Breite b	Flächeninhalt A	Umfang U
a)	5 cm	7 dm
b)	30 cm			1,4 m
c)		120 m	6 ha
d)	80 cm		4 m²

	Länge l	Breite b	Flächeninhalt A	Umfang U
a)	5 cm	7 dm	3,5 dm²	15dm
b)	30 cm	0,4 m	0,12 m²	1,4 m
c)	500 m	120 m	6 ha	1240 m
d)	80 cm	5 m	4 m²	11,6 m

Ein Quadrat hat den Flächeninhalt $A_{Q} = 213444 {cm}^{2}$ . Ein Rechteck, in dem eine Seite doppelt so lang wie die andere ist, hat den gleichen Umfang wie das Quadrat. Welchen Flächeninhalt hat das Rechteck?

cm²

9
Aus einem Drahtstück wird ein Rechteck der Fläche $28 {cm}^{2}$ gebogen, wobei eine Seite des Rechtecks 4 cm lang ist. Welche Länge hat der Draht?
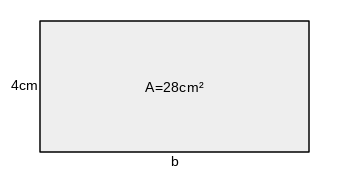cm

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
Zweite Seite berechnen:
$b = 28 {cm}^{2} : 4 cm = 7 cm$
Länge des Drahtes:
$x = 2 \cdot (4 cm + 7 cm) = 22 cm$
10
Durch Aneinanderlegen von 24 quadratischen Teppichfliesen soll eine lückenlose rechteckige Spielfläche gebildet werden. Jede Teppichfliese hat 0,5m Seitenlänge. Maria hat ein Rechteck mit 6 Fliesen an einer Längsseite und 4 Fliesen an einer Breitseite gelegt. Berechne den Umfang und den Flächeninhalt der Spielfläche. Gib alle weiteren Möglichkeiten an, aus allen 24 Fliesen eine rechteckige Spielfläche zu legen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
$U = 2 \cdot (6 \cdot a) + 2 \cdot (4 \cdot a) = 12 \cdot a + 8 \cdot a = 20 \cdot a$
$U = 20 \cdot 0,5 m = 10 m$
$A = (6 \cdot a) \cdot (4 \cdot a) = 24 \cdot a^{2}$
$A = 24 \cdot (0,5 m)^{2} = 24 \cdot 0,25 m^{2} = 6 m^{2}$
Längsseite
1
2
3
4
6
8
12
24
Breitseite
24
12
8
6
4
3
2
1
11
Berechne den Flächeninhalt des Parallelogramms.
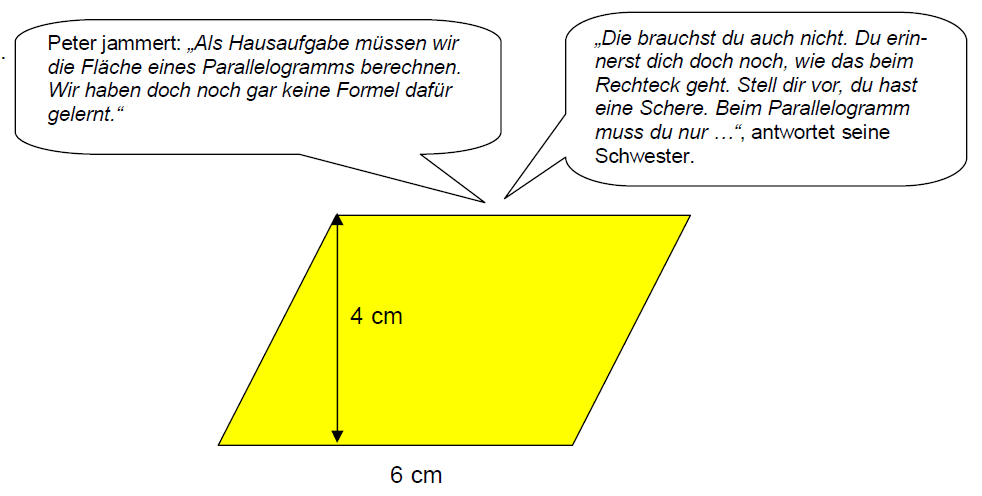cm²

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
So könnte der Satz zu Ende gehen:
"… an der einen Seite ein Dreieck wegschneiden und es an der gegenüber liegenden Seite anlegen, dann erhältst du ein Rechteck"
Am Beispiel der Zeichnung könnte man das Parallelogramm genau dort zerschneiden, wo der Doppelpfeil eingezeichnet ist.
Um den Flächeninhalt eines Parallelogramms zu berechnen, kann man also einfach eine Seite a und ihre Höhe h in die Formel zur Berechnung des Flächeninhalts eines Rechtecks einsetzen.
Hier:
$a = 6 cm, h = 4 cm$
Setze die Werte in die Formel ein.
$A = 6 cm \cdot 4 cm$
$A = 24 {cm}^{2}$
12
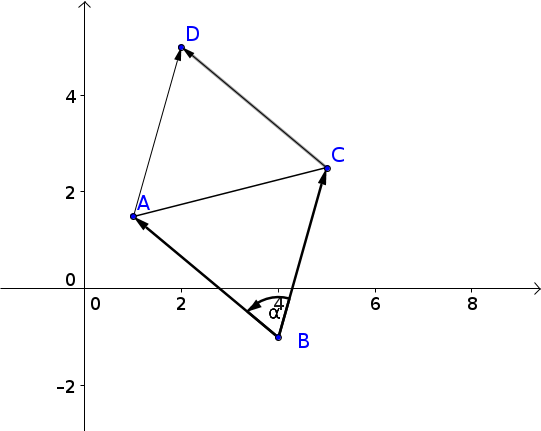
Berechne die Fläche des Parallelogramms, das von den angegebenen Punkten aufgespannt wird.
1. $A (1 | 1,5); B (4 | - 1); C (5 | 2,5)$
  FE
  
  Für diese Aufgabe benötigst du - je nach Lösungsweg - Grundwissen über die Determinante oder über das Kreuzprodukt.
  $A (1 | 1,5); B (4 | - 1); C (5 | 2,5)$
  Zeichne die Punkte in ein Koordinatensystem ein, um einen Überblick zu erhalten. Es ist nicht nötig, das Parallelogramm aus den angegeben Punkt zu konstruieren, da es nur zwei Vektoren benötigt, um die Fläche zu berechnen. Wähle eine Ecke, von der die Vektoren das Parallelogramm aufspannen, und berechne diese Vektoren.
  Auch hier ist es egal, welche Ecke man wählt, da die Parallelogrammfläche stets das Doppelte der gewählten Dreiecksfläche ist.
  $\vec{B A} = (\begin{array}{c} 1 - 4 \\ 1,5 - (- 1) \end{array}) = (\begin{array}{c} - 3 \\ 2,5 \end{array})$
  $\vec{B C} = (\begin{array}{c} 5 - 4 \\ 2,5 - (- 1) \end{array}) = (\begin{array}{c} 1 \\ 3,5 \end{array})$
  1. Lösungsweg: Flächenberechnung mit Determinante
  Bestimme die Reihenfolge der Vektoren in der Determinante gegen den Uhrzeigersinn ( $α$ ) oder setze um die Determinante einen Betrag.
  Wichtig: KEIN $\frac{1}{2}$ !
  Berechne die Determinante und erhalte dann das Ergebnis. Flächeneinheit dabei nicht vergessen, wenn gefordert.
  $A = | | \begin{array}{cc} \vec{BA} & \vec{BC} \end{array} | | = | \begin{array}{cc} \vec{BC} & \vec{BA} \end{array} | = | \begin{array}{cc} 1 & - 3 \\ 3,5 & 2,5 \end{array} | = 2,5 + 10,5 = 13 F E$
  2. Lösungsweg: Flächenberechnung mit Kreuzprodukt
  Bette die Zeichenebene in den $ℝ^{3}$ ein. Dies geschieht, indem jedem Vektor als dritte Komponente der Eintrag $0$ hinzugefügt wird.
  Berechne nun das Kreuzprodukt $\vec{B A} \times \vec{B C}$ . Das Ergebnis ist ein zu $\vec{B A}$ und $\vec{B C}$ orthogonaler Vektor, dessen Betrag dem Flächeninhalt des von $\vec{B A}$ und $\vec{B C}$ aufgespannten Parallelogramms entspricht.
  $A = | \vec{B A} \times \vec{B C} | = | (\begin{array}{c} - 3 \\ 2,5 \\ 0 \end{array}) \times (\begin{array}{c} 1 \\ 3,5 \\ 0 \end{array}) | = | (\begin{array}{c} 0 \\ 0 \\ - 13 \end{array}) | = 13 F E$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
13
Die beiden parallelen Seiten eines Trapezes werden mit a und c bezeichnet, die Höhe mit h; für seinen Flächeninhalt gilt: $A = \frac{1}{2} \cdot (a + c) \cdot h$ .
Wie ändert sich der Flächeninhalt des Trapezes, wenn die Seite a um eine Längeneinheit verlängert und die Seite c um eine Längeneinheit verkürzt wird?
Die Fläche des Trapezes wird kleiner.
Die Fläche des Trapezes wird größer.
Die Fläche des Trapezes bleibt gleich groß.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Trapezes
$A_{T r a p e z} = \frac{1}{2} (a + 1 LE + c - 1 LE) \cdot h$
$1 LE$ fällt weg.
$A_{T r a p e z} = \frac{1}{2} (a + c) \cdot h$
$\Rightarrow$ Ausgangsformel für den Flächeninhalt eines Trapezes.
Die Fläche des Tapezes ändert sich bei einer Veränderung der beiden Grundseiten um $1 LE$ nicht.
Achtung: Die ursprüngliche Seitenlänge c muss allerdings länger als $1 LE$ sein, damit man sie um $1 LE$ verkürzen kann!
Dies gilt auch, wenn die eine der beiden Grundseiten um einen anderen bestimmten Betrag (kleiner als die Länge der kürzeren Seite) verlängert und die andere um denselben Wert verkürzt wird.
Versuche es zunächst mit einem Zahlenbeispiel.
14
Die Nationalfahne der Schweiz zeigt ein weißes Kreuz auf rotem Grund. Für die vier kongruenten Arme des Kreuzes ist durch Beschluss der Schweizer Bundesversammlung aus dem Jahr 1889 festgelegt: Die Länge $l$ eines Arms ist um $\frac{1}{6}$ der Breite $b$ größer als $b$ (vergleiche Abbildung).
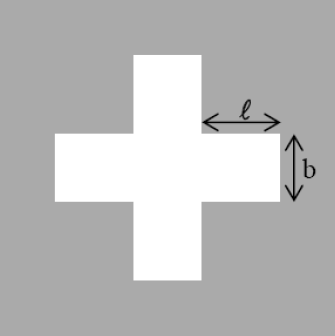
1. Wie lang ist ein Arm, wenn seine Breite $18 c m$ beträgt?
  cm
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Rechteck
  Breite $b = 18 cm$
  Stelle eine Gleichung für die Länge $l$ auf.
  Länge $l$ ist um $\frac{1}{6}$ länger als $b$
  $l$ $=$ $\frac{7}{6} \cdot b$
  ↓
  Setze den gegebenen Zahlenwert für $b$ ein.
  $l$ $=$ $\frac{7}{6} \cdot 18 c m$
  $l$ $=$ $21 c m$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Stelle einen Term auf, der den Flächeninhalt des weißen Kreuzes in Abhängigkeit von der Breite b eines Arms beschreibt. Fasse den Term, in dem nur noch $b$ als Variable vorkommen soll, so weit wie möglich zusammen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Rechteck
  $A = 4 \cdot b \cdot l + b^{2}$
  Stelle eine Gleichung für den Flächeninhalt auf. Ersetze die Breite $b$ durch das Ergebnis für die Länge $l$ aus der 1. Teilaufgabe
  $= 4 \cdot b \cdot (\frac{7}{6} b) + b^{2}$
  Vereinfache soweit wie möglich.
  $= \frac{17}{3} b^{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Längsseite	1	2	3	4	6	8	12	24
Breitseite	24	12	8	6	4	3	2	1

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$A$	$=$	$l \cdot b$
	↓	Setze die gegebenen Zahlenwerte für $l$ und $A$ ein.
$1470 m^{2}$	$=$	$21 m \cdot b$
	↓	Löse die Gleichung nach $b$ auf.
$b$	$=$	$\frac{1470 m^{2}}{21 m} = 70 m$
	↓	Berechne mit diesem Ergebnis den Umfang.

$U$	$=$	$2 b + 2 l$
	↓	Setze die Zahlenwerte ein.
$U$	$=$	$2 \cdot 70 m + 2 \cdot 21 m$
$U$	$=$	$182 m$

$U$	$=$	$4 \cdot 462 cm = 1848 cm$
	↓	Berechne den Umfang aus der Seitenlänge $a_{Q}$ des Quadrats.
$U$	$=$	$2 a + 2 b$
	↓	Berechne den Umfang des Rechtecks. Benutze, dass $a = 2 \cdot b$ ist.
$U$	$=$	$2 \cdot (2 \cdot b) + 2 \cdot b = 4 \cdot b + 2 \cdot b$
$U$	$=$	$4 \cdot b + 2 \cdot b$
$U$	$=$	$6 \cdot b$
	↓	Forme nach b um.

$l$	$=$	$\frac{7}{6} \cdot b$
	↓	Setze den gegebenen Zahlenwert für $b$ ein.
$l$	$=$	$\frac{7}{6} \cdot 18 c m$
$l$	$=$	$21 c m$

Aufgaben zu Flächen von Dreiecken und Vierecken

a) Berechnung Flächeninhalt A und Umfang U

b) Berechnung Breite b und Flächeninhalt A

c) Berechnung Länge l und des Umfang U

d) Berechnung Breite b und Umfang U

Seitenlänge des Grundstücks

Umfang des Grundstücks

Variable einführen

Gleichung aufstellen

Gleichung lösen

Lösung überprüfen:

Antwortsatz

1. Lösungsweg: Flächenberechnung mit Determinante

2. Lösungsweg: Flächenberechnung mit Kreuzprodukt

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?