Analysis, Teil A, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Zeigen Sie, dass der Graph der in $\mathbb{R}$ definierten Funktion $g: x \mapsto x^2 \cdot sin(x)$ punktsymmetrisch bezüglich des Koordinatenursprungs ist, und geben Sie den Wert des Integrals $\int_{-\pi}^\pi{x^2\cdot sin(x)}\text{d}x$ an. (3 BE)
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
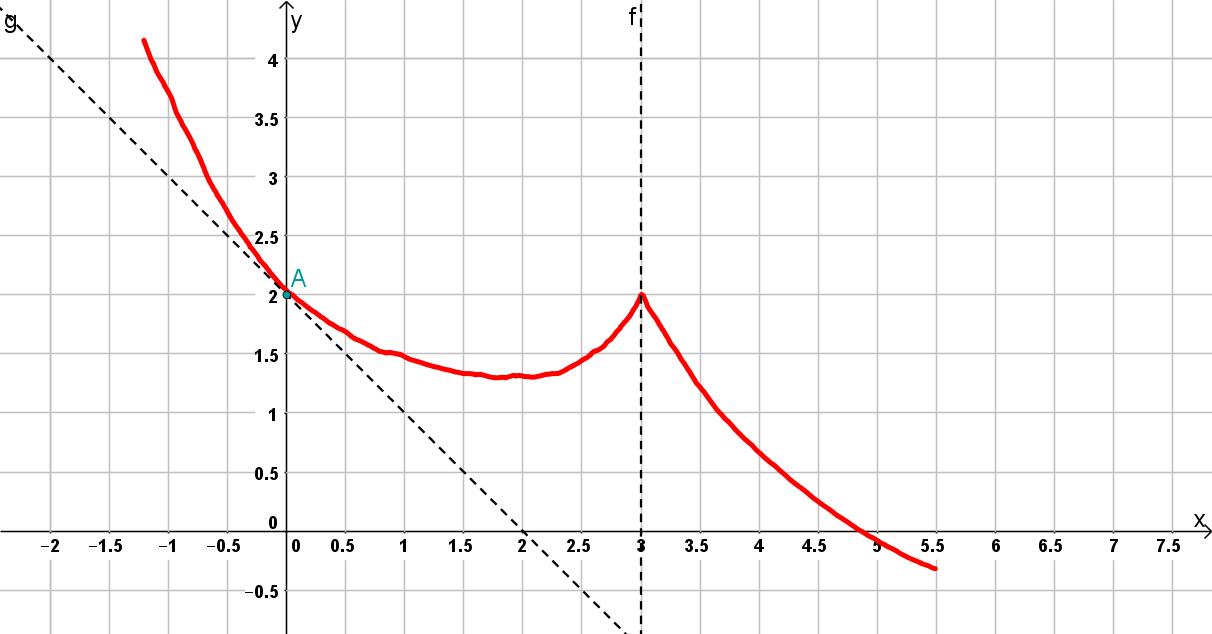
Skizzieren Sie im Bereich $-1\leq x\leq4$ den Graphen einer in $\mathbb{R}$ definierten Funktion $f$ mit den folgenden Eigenschaften:
- $f$ ist nur an der Stelle $x=3$ nicht differenzierbar.
- $f(0)=2$ und für die Ableitung $f'$ von $f$ gilt: $f'(0)=-1$
- Der Graph von $f$ ist im Bereich $-1< x < 3$ linksgekrümmt.
(3 BE)
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Funktion $f: x \mapsto \sqrt {1-\ln(x)}$ mit maximaler Definitionsmenge $D$ .
1. Bestimmen Sie $D$ . (2 BE)
2. Bestimmen Sie den Wert $x \in D$ mit $f(x)=2$ . (2 BE)
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist eine in $\mathbb{R}$ definierte ganzrationale Funktion $f$ dritten Grades, deren Graph $G_f$ an der Stelle $x=1$ einen Hochpunkt und an der Stelle $x=4$ einen Tiefpunkt besitzt.
1. Begründen Sie, dass der Graph der Ableitungsfunktion $f'$ von $f$ eine Parabel ist, welche die $x$ -Achse in den Punkten $(1|0)$ und $(4|0)$ schneidet und nach oben geöffnet ist. (3BE)
2. Begründen Sie, dass $2{,}5$ die $x$ -Koordinate des Wendepunkts von $G_f$ ist. (2 BE)
5
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
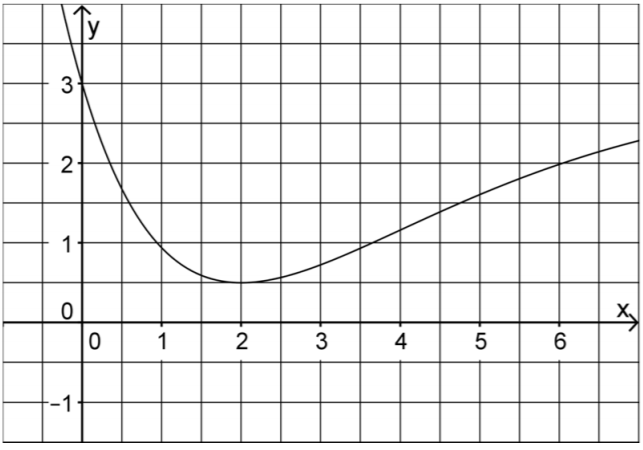
Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ .
1. Bestimmen Sie mithilfe der Abbildung einen Näherungswert für $\int_3^5{f(x)\text{d}}x$ . (2 BE)
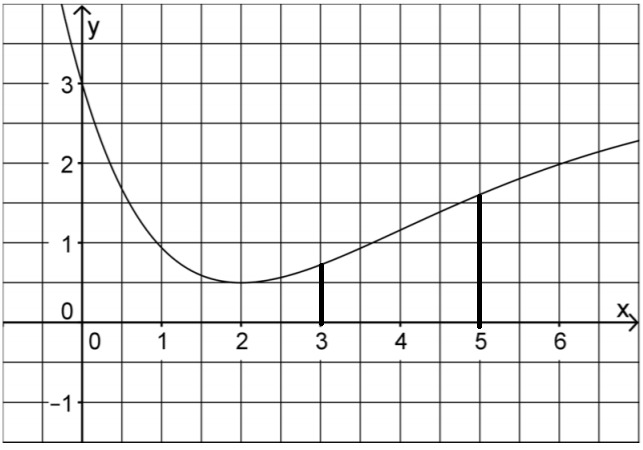
2. Die Funktion $F$ ist die in $\mathbb{R}$ definierte Stammfunktion von $f$ mit $F(3)=0$ .
  Geben Sie mithilfe der Abbildung einen Näherungswert für die Ableitung von $F$ an der Stelle $x=2$ an. (1 BE)
3. Zeigen Sie, dass $F(b)=\int_3^b{f(x)\text{d}}x$ mit $b \in \mathbb{R}$ gilt. (2 BE)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?