Teil B, Gruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

Löse folgende Gleichung.

$11 x - 3,5 \cdot (2 x - 4) = \frac{12 \cdot (x + 6)}{3} - \frac{3 x}{2} + 8$

Punkte:4

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Zeichne ein Koordinatensystem mit der Einheit $1 c m$ .
Punkte: 3
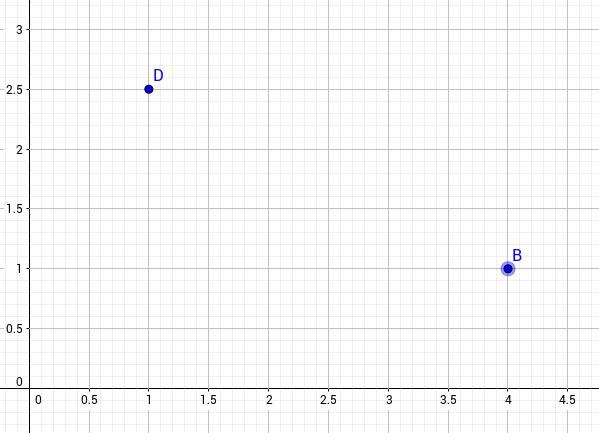
1. Trage die Punkte $B (4 | 1)$ und $D (1 | 2,5)$ ein.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem zeichnen.
  Für diese Aufgabe musst du ein Koordinatensystem zeichnen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Die Punkte $B$ und $D$ sind Eckpunkte einer Raute $A B C D$ . Eine Seitenlänge der Raute beträgt $5 c m$ . Zeichne die Raute.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Raute
  Überlege dir wie die Raute aussehen muss. Zeichne nun jeweils einen Kreis um die Punkte $B$ und $D$ mit dem Radius von $5 c m$ . Zeichne an den Stellen, an denen sich die Kreise schneiden, die Punkte A und C. Wenn du nun alle Punkte verbindest, erhältst du eine Raute.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Punkte: 4
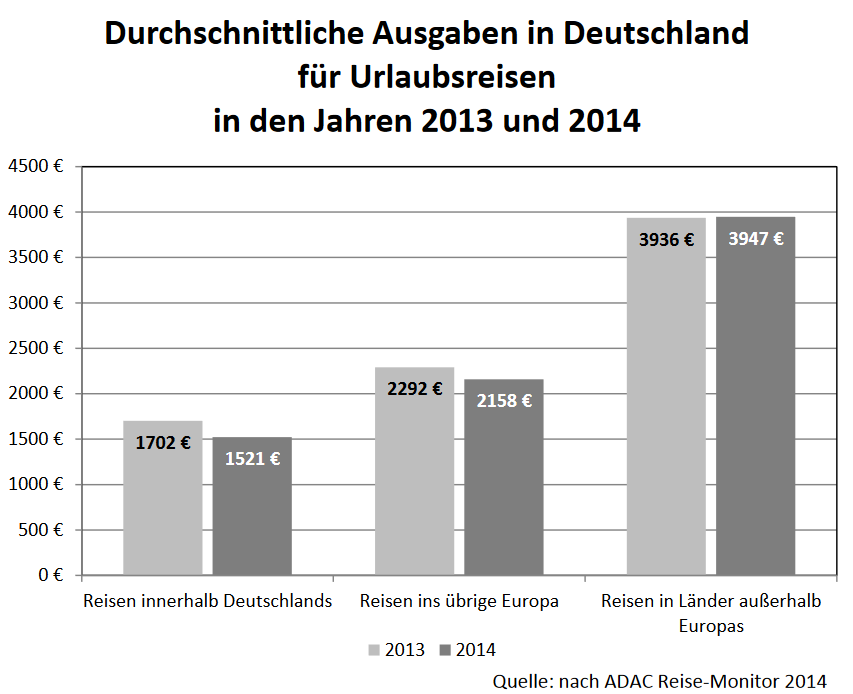
1. Um wie viel Prozent verändern sich die Ausgaben für einen Urlaub innerhalb Deutschlands von 2013 auf 2014?
  % Veränderung
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentrechnung
  Videolösung der gesamten Aufgabe
  Textlösung
  Die Ausgaben für Reisen sind innerhalb von Deutschland von 2013 auf 2014 von $1702 €$ auf $1521 €$ gesunken. Berechne die Differenz der beiden Werte.
  $1702 € - 1521 € = 181 €$
  Berechne mithilfe des Dreisatzes den Prozentsatz, um den die Ausgaben gesunken sind.
  $181 € \cdot 100 % : 1702 € \approx 10,63 %$
  $\Rightarrow$ Die Ausgaben für Reisen innerhalb von Deutschland sind von 2013 bis 2014 um $10,63 %$ gesunken.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Stelle die Ausgaben für Urlaubsreisen innerhalb Deutschlands und ins übrige Europa sowie für Länder außerhalb Europas für das Jahr 2013 in einem Kreisdiagramm anteilig dar (Radius $3 c m$ ).
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisdiagramm
  Zu Beginn musst du berechnen, welcher Winkel den jeweiligen Kategorien entspricht. Addiere dazu zunächst die Ausgaben im Jahr 2013 der einzelnen Kategorien.
  $1702 € + 2292 € + 3936 € = 7936 €$
  Dieser Wert würde dem ganzen Kreis entsprechen - also $360 °$ . Mithilfe des Dreisatzes kannst du die Größen der einzelnen Kategorien berechnen.
  Reisen innerhalb Deutschlands (D) :
  $1702 € \cdot 360 ° : 7930 € \approx 77 °$
  Reisen ins übrige Europa (E) :
  $2292 € \cdot 360 ° : 7930 € \approx 104 °$
  Reisen in Länder außerhalb Europas (W) :
  $3936 € \cdot 360 ° : 7930 € \approx 179 °$
  Da du in einigen Fällen runden musstest, solltest du deine Ergebnisse nochmal überprüfen, indem du alle Winkel addierst. Dein Ergebnis sollte dann in etwa $360 °$ ergeben.
  $77 ° + 104 ° + 179 ° = 360 ° ✓$
  Jetzt kannst du mithilfe der Winkel ein Kreisdiagramm zeichnen.
  Zeichen zu Beginn einen Kreis mit dem Radius $3 c m$ und markiere den Mittelpunkt.
  Zeichne einen Gerade vom Mittelpunkt zu einem belibigen Punkt auf dem Kreis. In unserem Fall verläuft diese senkrecht nach oben. Nun kannst du mit Hilfe eines Geodreiecks den ersten Winkel von $77 °$ einzeichnen.
  An der dadurch entstandene Gerade, kannst du den nächsten Winkel ( $104 °$ ) einzeichnen.
  Der letzte Winkel ergibt sich nun von alleine und muss nur noch markiert werden.
  Videolösung der gesamten Aufgabe
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
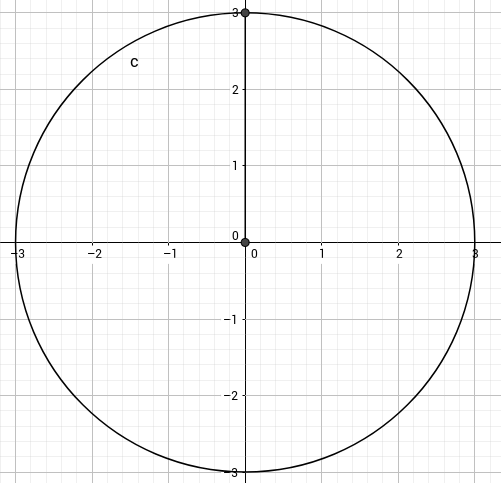
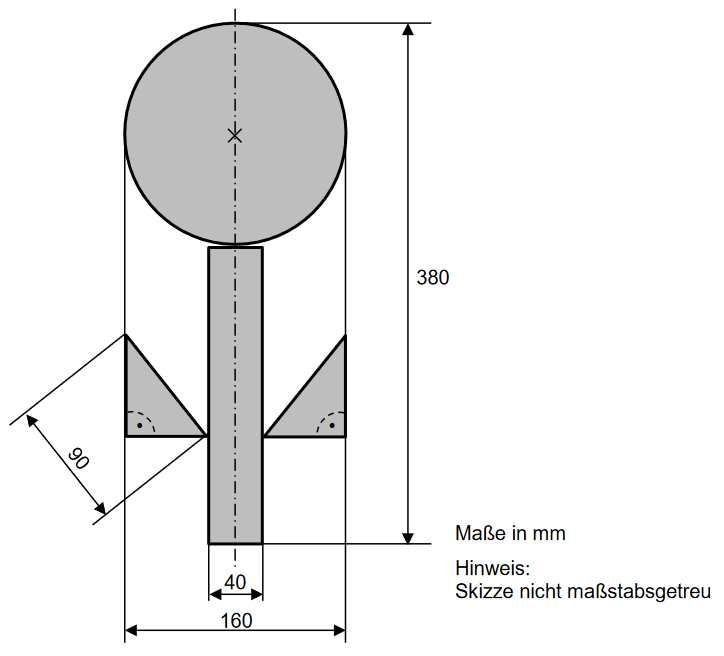
Die Theatergruppe einer Mittelschule druckt für das Bühnenbild einfache achsensymmetrische Blumen (siehe Szizze) auf Stoff.
Berechne den Flächeninhalt einer solchen Blume.
Punkte: 5

Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras
Außerdem benötigst du die Flächenformeln für Dreiecke, Rechtecke und Kreise.
Berechne nacheinander den Flächeninhalt der Teilfiguren und addiere am Schluss.
Kreis
Aus der Skizze kannst du ablesen, dass der Kreis einen Durchmesser von $160$ hat. Teile diesen Wert durch 2, um deinen Radius zu erhalten.
$160 𝕞 𝕞 : 2 = 80 𝕞 𝕞$ $\Rightarrow$ Der Radius beträgt also $80 𝕞 𝕞$ .
Nun kannst du den Flächeninhalt des Kreises mit der Formel $A_{K} = π \cdot r^{2}$ berechnen.
$A_{K} = π \cdot r^{2} = 3,14 \cdot (80 𝐦 𝐦)^{2} = 3,14 \cdot 80 𝐦 𝐦 \cdot 80 𝐦 𝐦 = 20096^{} {𝐦 𝐦}^{2}$ $\Rightarrow$ Die Fläche des Kreises beträgt $20096 {𝐦 𝐦}^{2}$ .
Dreieck
Da es sich um eine achsensymmetrische Figur handelt, müssen beide Dreiecke gleich groß sein. Eine Seite (die Hypotenuse) des Dreiecks ist gegeben ( $90 𝕞 𝕞$ ). Die zweite Seite (a), eine der Katheten, kannst du mit Hilfe der Angaben berechnen.
$160 𝕞 𝕞 - 40 𝕞 𝕞 = 120 𝕞 𝕞$ $120 𝕞 𝕞 : 2 = 60 𝕞 𝕞$ $\Rightarrow$ Die Seite a des Dreiecks beträgt $60 𝕞 𝕞$ .
Die letzte Seite (b) kannst du nun mit Hilfe des Satz des Pythagoras berechnen.
$a^{2} + b^{2} = c^{2}$
Setze die Werte für $a$ und $c$ ein.
$(60 𝕞 𝕞)^{2} + b^{2} = (90 𝕞 𝕞)^{2} | - (60 𝕞 𝕞)^{2}$
Stelle nach $b^{2}$ um.
$b^{2} = (90 𝕞 𝕞)^{2} - (60 𝕞 𝕞)^{2}$
Ziehe die Wurzel
$b = \sqrt{4500 {𝕞 𝕞}^{2}} \approx 67,1 𝕞 𝕞$
Berechne nun den Flächeninhalt des Dreiecks mit der Formel $A = 0,5 \cdot a \cdot h$ . In diesem Fall entspricht die Höhe h der Seite b, da bei C rechter Winkel ist. Außerdem musst du dein Ergebnis noch mit $2$ muliplizieren, um die Fläche beider Dreiecke zu erhalten.
$A = 0,5 \cdot 60 𝕞 𝕞 \cdot 67,1 𝕞 𝕞 = 2013 {𝕞 𝕞}^{2}$ $2013 {𝕞 𝕞}^{2} \cdot 2 = 4026 {𝕞 𝕞}^{2}$ $\Rightarrow$ Beide Dreiecke zusammen haben eine Fläche von $4026 {𝕞 𝕞}^{2}$ .
Rechteck
Zulezt musst du die Fläche des Rechtecks berechnen. Hierbei hast du eine Länge (a) gegeben ( $40 𝕞 𝕞$ ). Die 2. Länge (b) kannst du berechnen, indem du den Durchmesser des Kreises ( $160 𝕞 𝕞$ ) von der Länge der gesammten Figur ( $380 𝕞 𝕞$ ) abziehst.
$380 𝕞 𝕞 - 160 𝕞 𝕞 = 220 𝕞 𝕞$
$\Rightarrow$ Die Seite b ist $220 𝕞 𝕞$ lang.
Mit diesen Werten und der Formel $A = a \cdot b$ kannst du nun den Flächeninhalt des Rechtecks berechnen.
$A = 40 𝕞 𝕞 \cdot 220 𝕞 𝕞 = 8800 𝕞 𝕞^{𝟚}$
$\Rightarrow$ Die Fläche des Rechtecks beträgt $8800 {𝕞 𝕞}^{2}$ .
Gesamtfläche
Um nun die Fläche der gesammten Figur zu erhalten, musst du alle Flächeninhalte miteinander addieren.
$A = 20096 {𝕞 𝕞}^{2} + 4026 {𝕞 𝕞}^{2} + 8800 {𝕞 𝕞}^{2} = 32922 {𝕞 𝕞}^{2}$ $\Rightarrow$ Insgesammt hat die Figur einen Flächeninhalt von $32922 {𝕞 𝕞}^{2}$ .
Videoerklärung

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$11 x - 3,5 \cdot (2 x - 4)$	$=$	$\frac{12 \cdot (x + 6)}{3} - \frac{3 x}{2} + 8$
	↓	Kürze den ersten Bruch, schreibe den zweiten Bruch in einen Dezimalbruch um.
$11 x - 7 x + 14$	$=$	$4 \cdot (x + 6) - 1,5 x + 8$
	↓	Multipliziere die Klammern aus.
$4 x + 14$	$=$	$4 x + 24 - 1,5 x + 8$
	↓	Addiere auf der rechten Seite jeweils die Summanden ohne $x$ und die Summanden mit $x$
$4 x + 14$	$=$	$2,5 x + 32$	$- 14$
	↓	Subtrahiere auf beiden Seiten 14.
$4 x x$	$=$	$2,5 x + 18$	$- 2,5 x$
	↓	Subtrahiere auf beiden Seiten $2,5 x$ .
$1,5 x$	$=$	$18$	$: 1,5$
	↓	Teile durch den Faktor vor $x$ .
$x$	$=$	$12$

Teil B, Gruppe 2

11x−3,5⋅(2x−4)=12⋅(x+6)3−3x2+8

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Videolösung der gesamten Aufgabe

Textlösung

Hast du eine Frage oder Feedback?

Videolösung der gesamten Aufgabe

Hast du eine Frage oder Feedback?

Kreis

Dreieck

Rechteck

Gesamtfläche

$11 x - 3,5 \cdot (2 x - 4) = \frac{12 \cdot (x + 6)}{3} - \frac{3 x}{2} + 8$