Aufgaben zur Vierfeldertafel
- 1
Ein Betreiber eines Eisenbahnunternehmens hat eine Umfrage unter seinen Fahrgästen durchgeführt, die ergab, dass 10% der Fahrgäste in der ersten Klasse reisen. Außerdem wurde in der Umfrage abgefragt, wie zufrieden die Fahrgäste mit dem Service des Unternehmens sind. Hoch erfreut stellt das Unternehmen fest, dass der Fahrgäste zweiter Klasse zufrieden sind. Alarmierend dagegen sind die Zufridenheitszahlen der ersten Klasse: 70% der Fahrgäste erster Klasse sind unzufrieden. Betrachtet werden folgende Ereignisse:
: "Ein Teilnehmer der Umfrage ist 1. Klasse-Fahrer."
: "Ein Teilnehmer der Umfrage ist mit dem Service des Unternehmens zufrieden."
Erstelle eine vollständig ausgefüllte Vierfeldertafel.
Als dem Geschäftsführer die Zufriedenheitszahlen der 1. Klasse mitgeteilt werden, ist dieser schockiert. Resigniert erklärt er, dass das Unternehmen es nicht geschafft habe, den Zufriedenheitswert von 77% der Fahrgäste aus dem Vorjahr zu verbessern. Hat er recht?
Tatsächlich stellt er fest, dass im Vorjahr 85% der Fahrgäste zweiter Klasse zufrieden waren und immerhin 45% der Fahrgäste erster Klasse. Damit haben sich beide Werte in diesem Jahr verschlechtert. Stelle diese Werte in Bezug zu deiner Antwort auf Teilaufgabe 2. Erstelle dazu auch eine Vierfeldertafel für das Vorjahr.
- 2
In der Serlo-Schule benutzen 81% der Schüler Serlo, um sich auf ihre Mathearbeiten vorzubereiten. 42% der Schüler sind zwischen 15 und 18 Jahre alt und nutzen Serlo. Sie versuchen im Zuge ihrer Tutorenarbeit Schüler im Alter von 12-14 Jahren dazu zu überreden Serlo auch zu nutzen. 11% der Schüler nutzen Serlo nicht und sind zwischen 12 und 14 Jahre alt. Diese Gruppe gilt es zu überzeugen.
Erstelle hierzu eine Vierfeldertafel.
- 3
Fülle mit den folgenden Informationen eine Vierfeldertafel aus!
- 4
Fülle mit den folgenden Informationen eine Vierfeldertafel mit absoluten Häufigkeiten aus!
In einer Schulklasse mit 29 Schüler*innen haben 10 Schüler*innen braune Haare und 7 Schüler*innen grüne Augen. 5 Schüler*innen haben grüne Augen und braune Haare.
Am Sportunterricht nehmen insgesamt 25 Kinder teil, wovon 15 weiblich sind. Genau 15 Kinder sind gut im Weitwurf. 10 Mädchen sind gut im Weitwurf.
Bei einer Versuchsreihe nehmen 47 Personen teil. 20 von diesen Personen wurden auf eine bestimmte Krankheit positiv getestet. 32 Testpersonen sind gegen diese Krankheit geimpft, wobei 15 Personen positiv getestet wurden und nicht dagegen geimpft sind.
In einer Firma arbeiten 45 Männer und 50 Frauen. 30 weibliche Mitarbeitende der Firma sind jünger als 50 Jahre und 27 Männer sind älter als 50 Jahre.
- 5
Ein Getränkeautomat ist defekt. Jemand wirft ein. Die Wahrscheinlichkeit dafür, dass er ein Getränk erhält, ist . Die Wahrscheinlichkeit dafür, dass der Apparat ein Getränk und den Euro wieder auswirft, ist . Die Wahrscheinlichkeit dafür, dass er kein Getränk bekommt und den Euro zurückerhält, ist .
Gib einen Ergebnisraum an.
Wie groß ist die Wahrscheinlichkeit dafür, dass man ein Getränk bekommt und es bezahlt hat?
Wie groß ist die Wahrscheinlichkeit dafür, dass man weder ein Getränk erhält, noch seinen Euro zurückbekommt?
Wie groß ist die Wahrscheinlichkeit dafür, dass man ein Getränk bekommt und trotzdem seinen Euro zurückbekommt?
Wie groß ist die Wahrscheinlichkeit dafür, dass man entweder ein Getränk erhält oder seinen Euro zurückbekommt?
- 6
Ein Betreiber eines Eisenbahnunternehmens hat eine Umfrage unter seinen Fahrgästen durchgeführt, die ergab, dass der Fahrgäste in der ersten Klasse reisen. Außerdem wurde in der Umfrage abgefragt, wie zufrieden die Fahrgäste mit dem Service des Unternehmens sind. Hoch erfreut stellt das Unternehmen fest, dass der Fahrgäste zweiter Klasse zufrieden sind. Alarmierend dagegen sind die Zufriedenheitszahlen der ersten Klasse: der Fahrgäste erster Klasse sind unzufrieden. Betrachtet werden folgende Ereignisse:
E: "Ein Teilnehmer der Umfrage ist 1.Klasse-Fahrer"
Z: "Ein Teilnehmer der Umfrage ist mit dem Service des Unternehmens zufrieden."
Erstelle eine vollständig ausgefüllte Vierfeldertafel.
Als dem Geschäftsführer die Zufriedenheitszahlen der 1.Klasse mitgeteilt werden, ist dieser schockiert. Resigniert erklärt er, dass das Unternehmen es nicht geschafft habe, den Zufriedenheitswert von % der Fahrgäste aus dem Vorjahr zu verbessern. Hat er Recht?
Tatsächlich stellt er fest, dass im Vorjahr der Fahrgäste zweiter Klasse zufrieden waren und immerhin der Fahrgäste erster Klasse. Damit haben sich beide Werte in diesem Jahr verschlechtert. Stelle diese Werte in Bezug zu deiner Antwort auf Teilaufgabe 2. Erstelle dazu auch eine Vierfeldertafel für das Vorjahr.
- 7
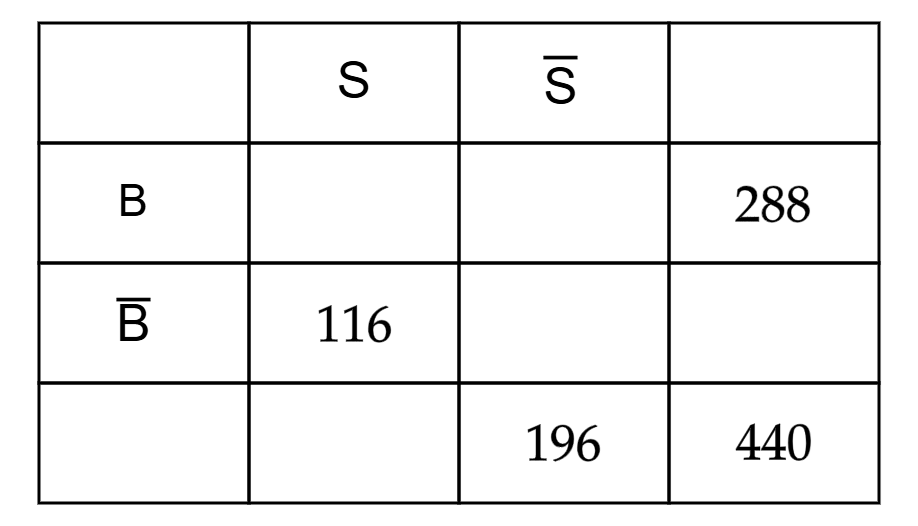
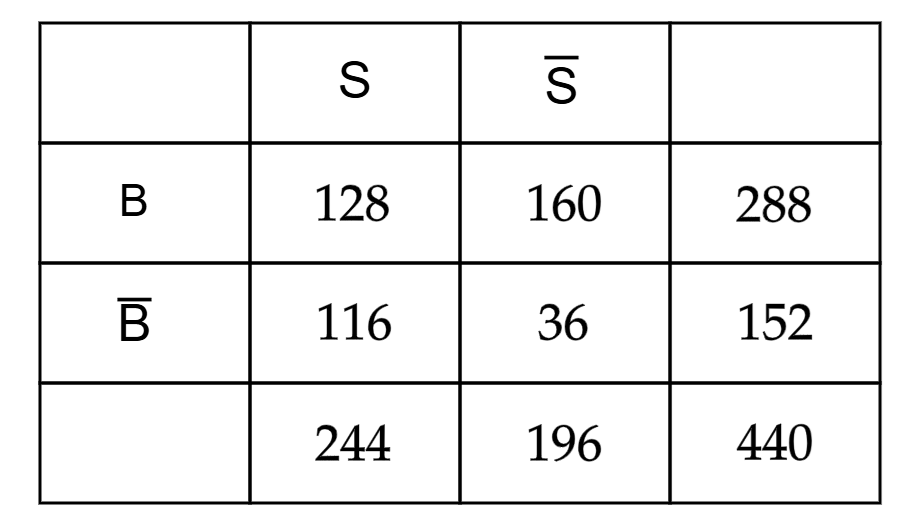
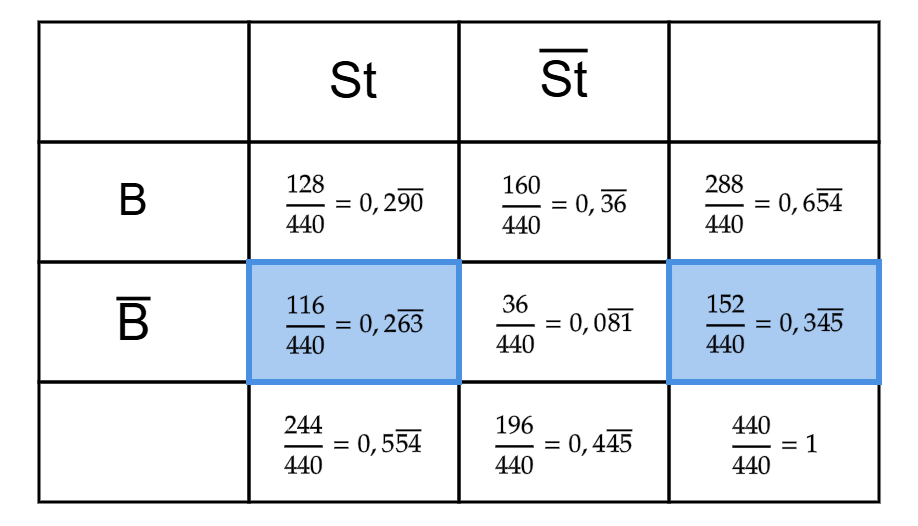
196 deiner 440 Facebook-Freunde haben ihren Beziehungsstatus nicht angegeben. Da du aber alle persönlich kennst, weißt du, dass insgesamt 288 deiner Facebook-Freunde in einer Beziehung sind. 116 derer, die ihren Beziehungsstatus angegeben haben, sind single.
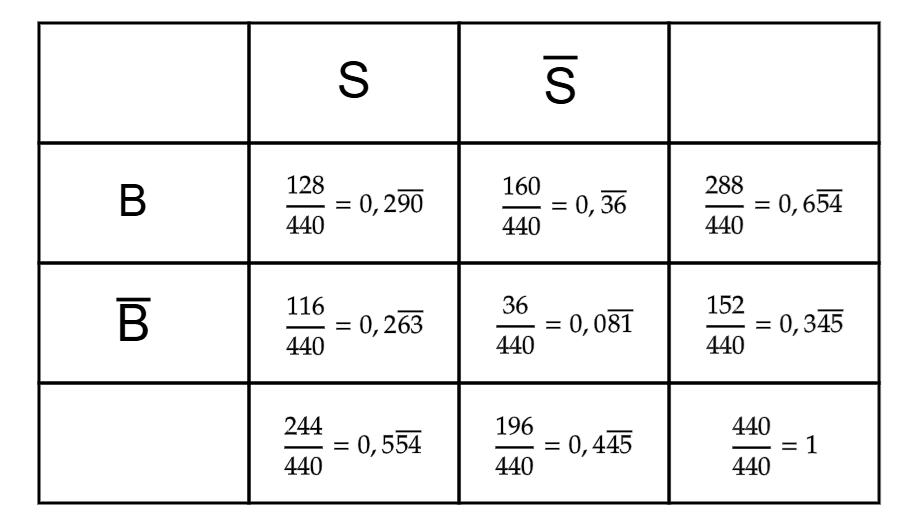
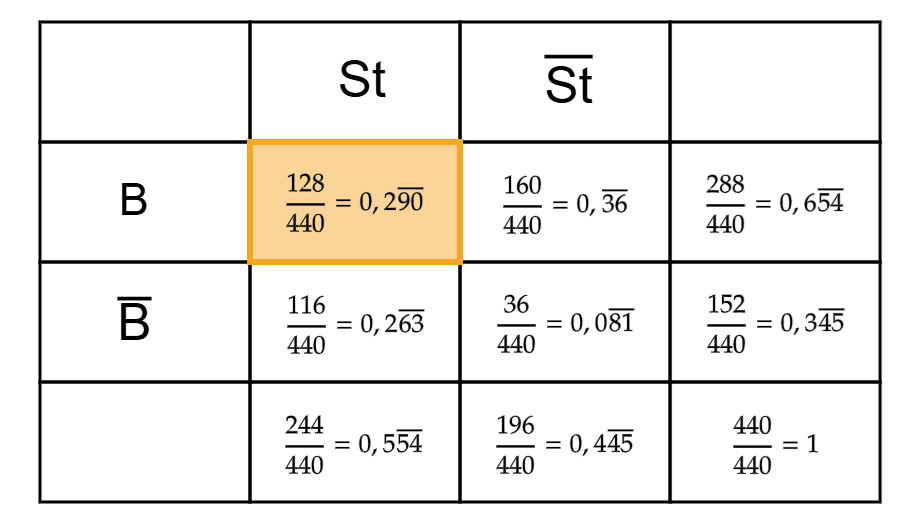
Berechne die Wahrscheinlichkeiten für die Vierfeldertafel, die du mit den Informationen aus dem Text ermitteln kannst. Übertrage diese dann in eine Vierfeldertafel.
Wie wahrscheinlich ist es, dass jemand in einer Beziehung ist und dies auch bei Facebook angibt?
Wie groß ist die Wahrscheinlichkeit, dass jemand, der Single ist, dies auch bei Facebook angibt?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?