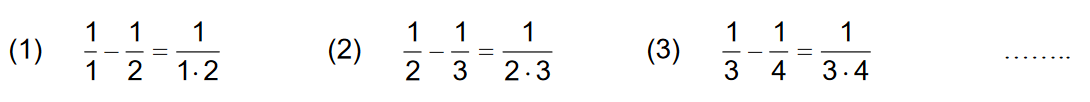Gruppe A
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
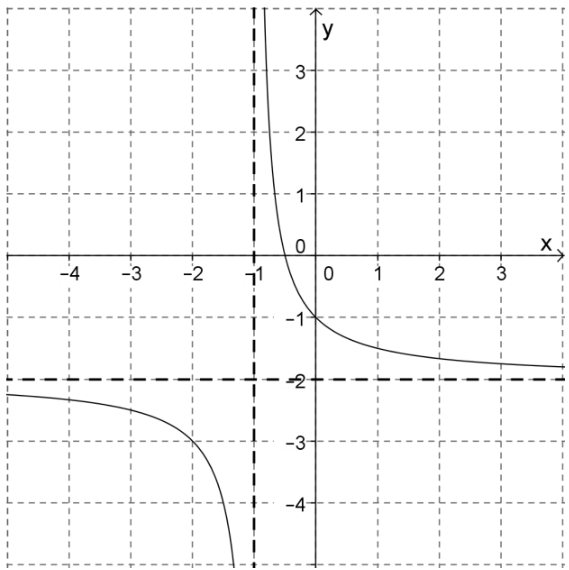
Die Abbildung zeigt den Graphen einer gebrochen-rationalen Funktion , der aus dem Graphen der Funktion mit Definitionsmenge durch Verschiebungen hervorgeht. Geben Sie einen passenden Funktionsterm für an. (2 BE)
- 2
Berechnen Sie jeweils alle Lösungen der Gleichung über der Grundmenge , ohne die Lösungsformel für quadratische Gleichungen zu verwenden. (je 1 BE)
a)
b)
- 3
Wahr oder falsch? Kreuzen Sie an. (2 BE)
- 4
An der Bliggspitze (3354m) in den Ötztaler Alpen besteht die Gefahr, dass ungefähr vier Millionen Kubikmeter Gestein in Richtung Tal abrutschen. Diese Gesteinsmenge lässt sich durch einen Würfel gleichen Volumens veranschaulichen. Kreuzen Sie denjenigen Wert an, der der Kantenlänge dieses Würfels am nächsten kommt. (1 BE)
- 5
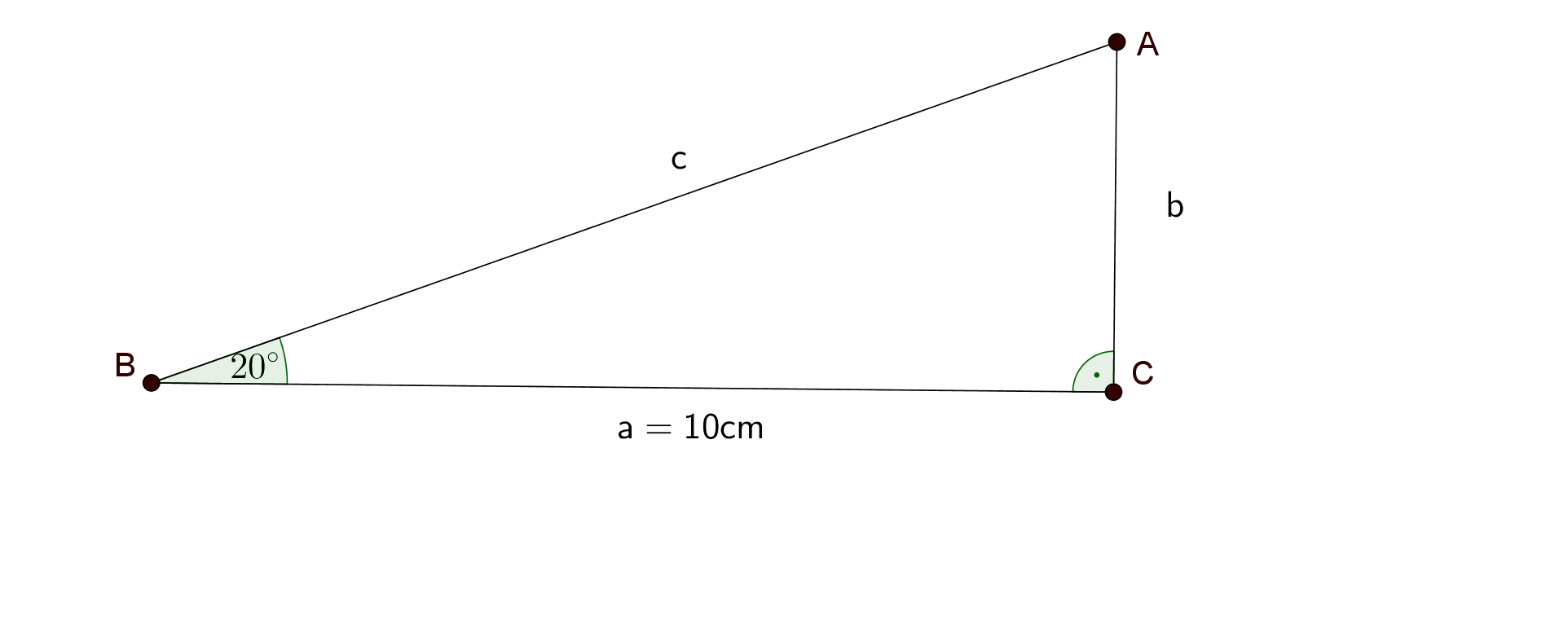
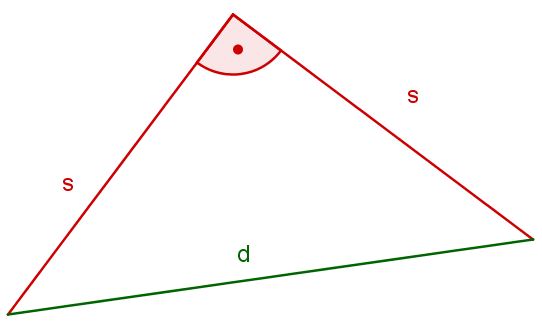
Bestimmen Sie für mithilfe einer beschrifteten Zeichnung sowie geeigneter Messungen einen möglichst genauen Näherungswert. Geben Sie Ihren Näherungswert in dezimaler Schreibweise mit zwei Nachkommastellen an. (2 BE)
- 6
Hannah schreibt eine Folge von Gleichungen auf:
Stellen Sie unter Verwendung einer Variablen eine möglichst einfache Gleichung auf, die für n=1, n=2 und n=3 die angegebenen Gleichungen (1), (2) bzw. (3) liefert.Untersuchen Sie, ob die von Ihnen aufgestellte Gleichung für jede beliebige natürliche Zahl n (n = 1, 2, 3, 4, 5, …) richtig ist. (2 BE)
- 7
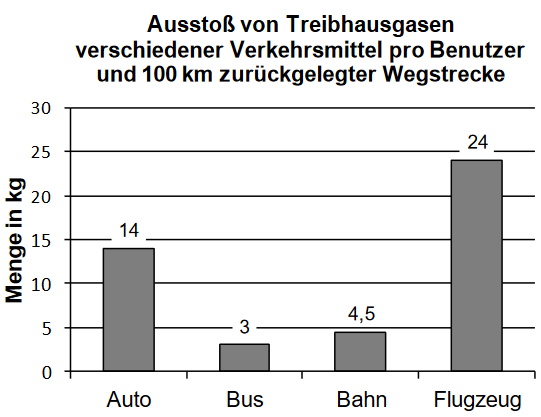
Verkehrsmittel stoßen weltweit eine große Menge von Treibhausgasen aus. Die Abbildung zeigt für verschiedene Verkehrsmittel, wie viele Kilogramm Treibhausgase durchschnittlich pro Benutzer und zurückgelegter Wegstrecke ausgestoßen werden.
Ermitteln Sie für das Verkehrsmittel Auto auf der Grundlage der Abbildung, wie viele Kilogramm Treibhausgase pro Benutzer und zurückgelegter Wegstrecke durchschnittlich ausgestoßen werden. (1 BE)
In der Abbildung ist für den Bus ein geringerer Wert angegeben als für das Auto. Machen Sie dies im Sachzusammenhang plausibel. (1 BE)
Bei der Erstellung der Abbildung wurde für das Flugzeug angenommen, dass auf jedem Flug der verfügbaren Plätze besetzt sind. Bestimmen Sie den Zahlenwert, der in der Abbildung für das Flugzeug angegeben werden müsste, wenn man annehmen würde, dass auf jedem Flug nur der Plätze besetzt sind. (2 BE)
- 8
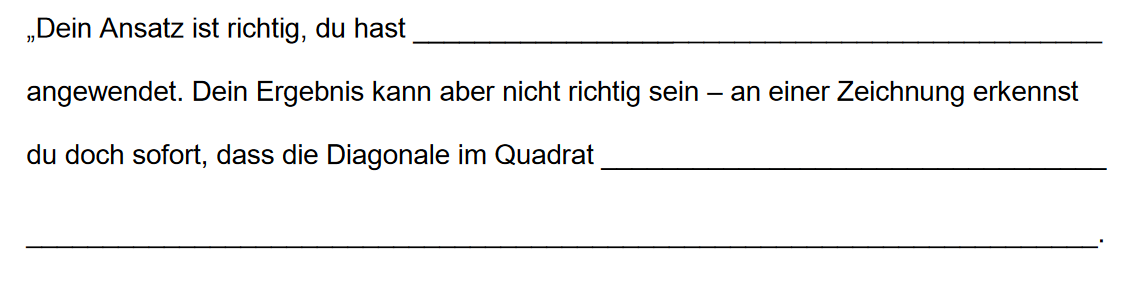
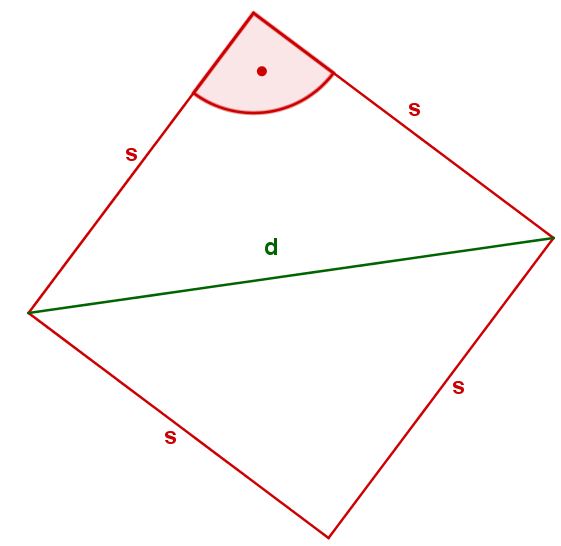
Maximilian soll für ein Quadrat der Seitenlänge einen möglichst einfachen Term für die Länge der Diagonale des Quadrats bestimmen. Er rechnet:
Maximilians Mitschülerin Sophie erkennt, dass seine Rechnung einen Fehler enthält.
Ergänzen Sie sinnvoll, was Sophie zu Maximilian sagen könnte (2 BE) :
Stellen Sie Maximilians Rechnung richtig, indem Sie den Term für korrekt umformen und so weit wie möglich vereinfachen (1 BE) :
- 9
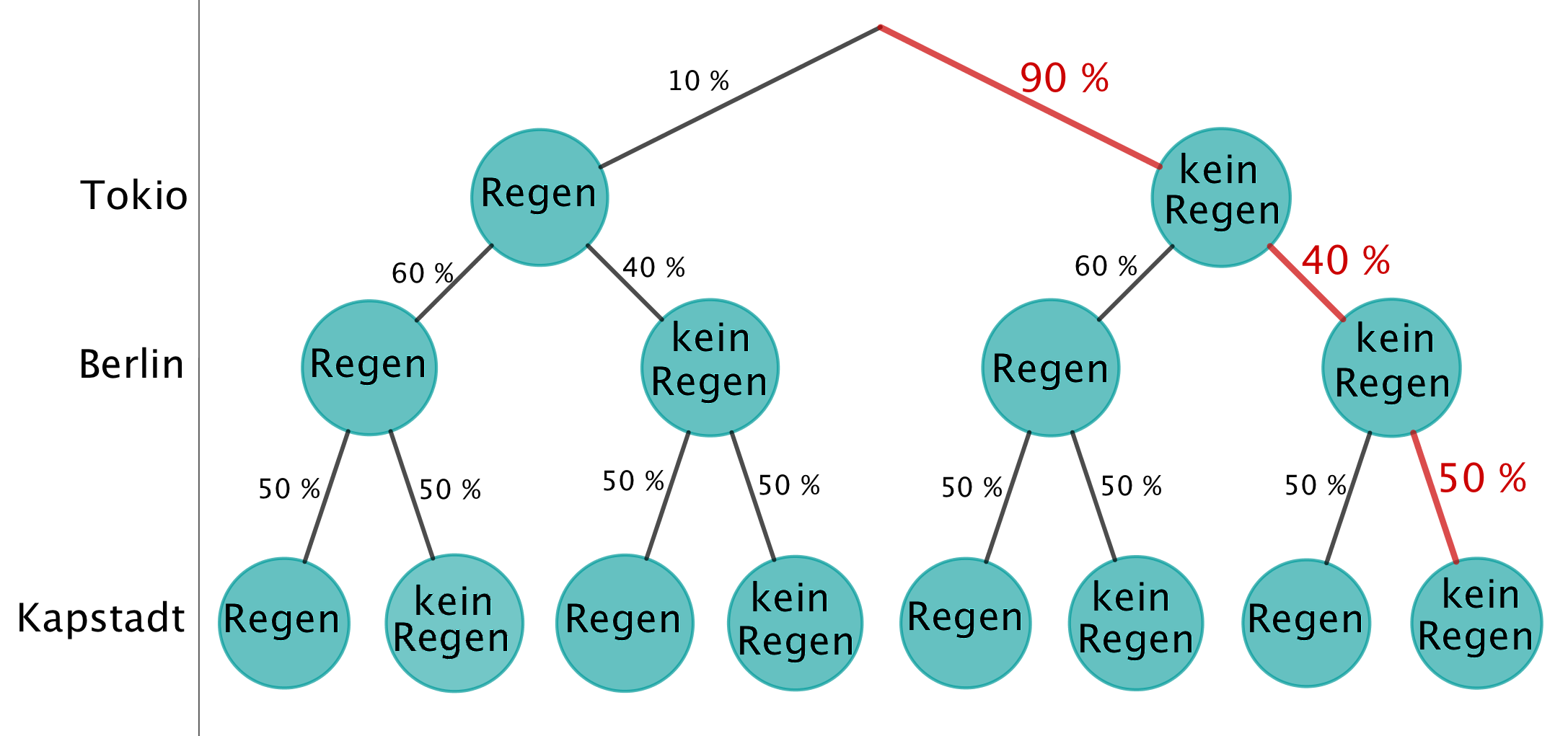
Für ein WM-Endspiel finden in Berlin, Kapstadt und Tokio Public-Viewing-Veranstaltungen statt. Im Internet findet man folgende Vorhersage, die sich auf das Wetter während des Spiels bezieht:
Zum Beispiel bedeutet die Angabe „“: Die Wahrscheinlichkeit dafür, dass es während des Spiels in Berlin mindestens einmal regnet (z. B. in Form eines Schauers), beträgt .
Geben Sie die Wahrscheinlichkeit dafür an, dass es während des Spiels in Tokio nicht regnet. (1 BE)
Berechnen Sie die Wahrscheinlichkeit (in Prozent) dafür, dass es während des Spiels in keiner dieser drei Städte regnet. (2 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?