Aufgaben zu Steigung und Differenzierbarkeit anhand des Graphen
Hier findest du Aufgaben zur Stetigkeit und Differenzierbarkeit. Lerne, anhand des Graphen Fragen zu beantworten und vertiefe dein Wissen!
- 1
Steigungen schätzen
Welche der drei Aussagen über die gezeichnete Funktion f stimmt?
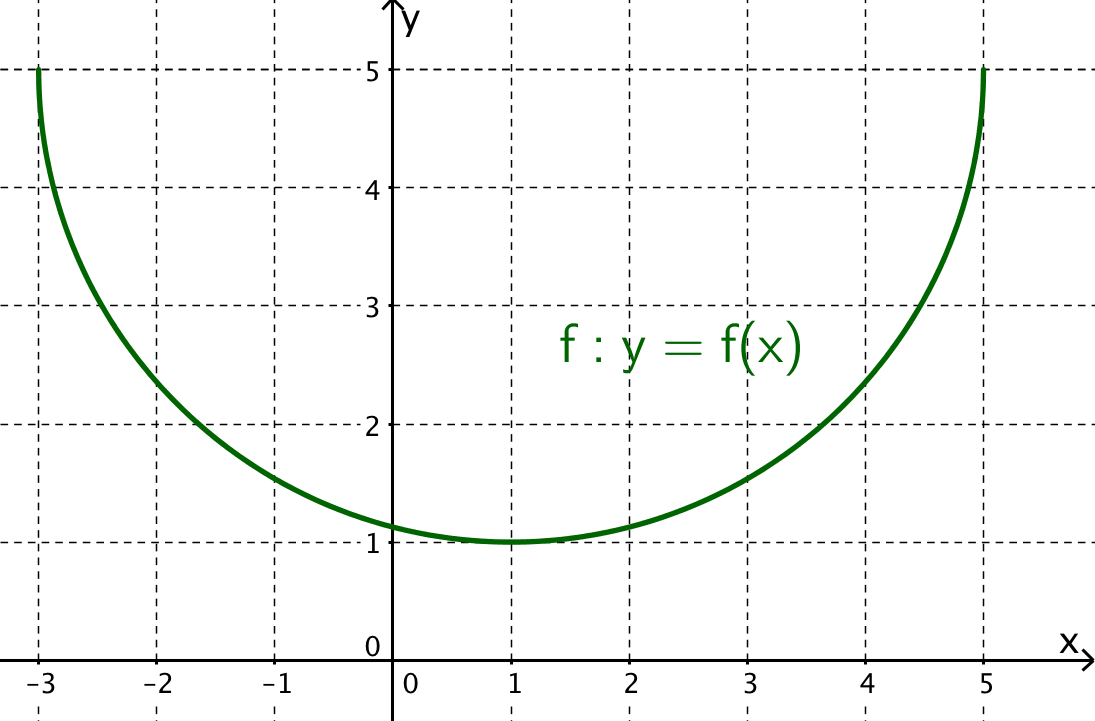
Welche Aussage über einen Ableitungswert der gezeichneten Funktion f stimmt?
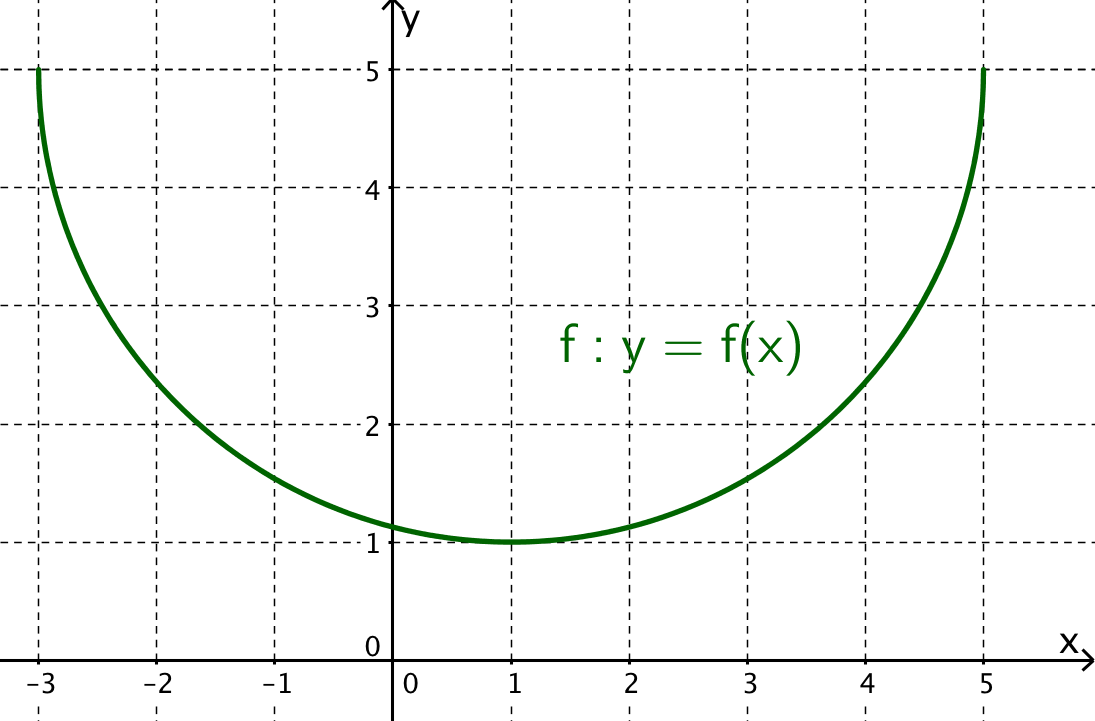
Welche der Aussagen über den Steigungswert der gezeichneten Funktion f stimmt?
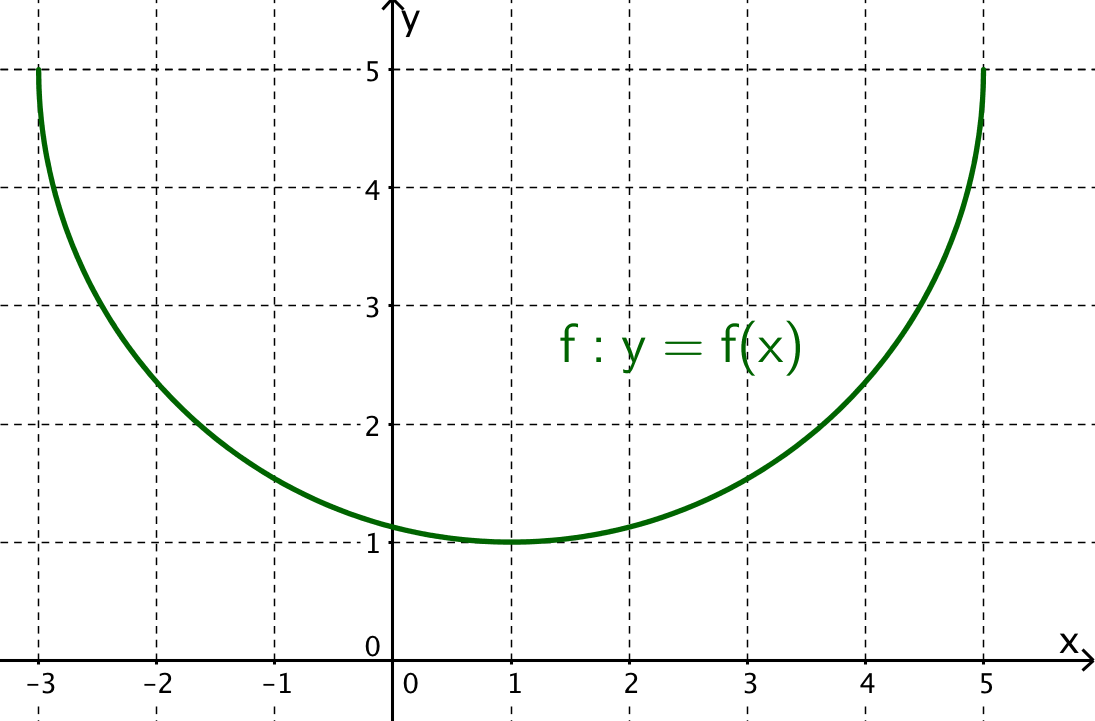
Welche der Aussagen über den Ableitungswert stimmen?
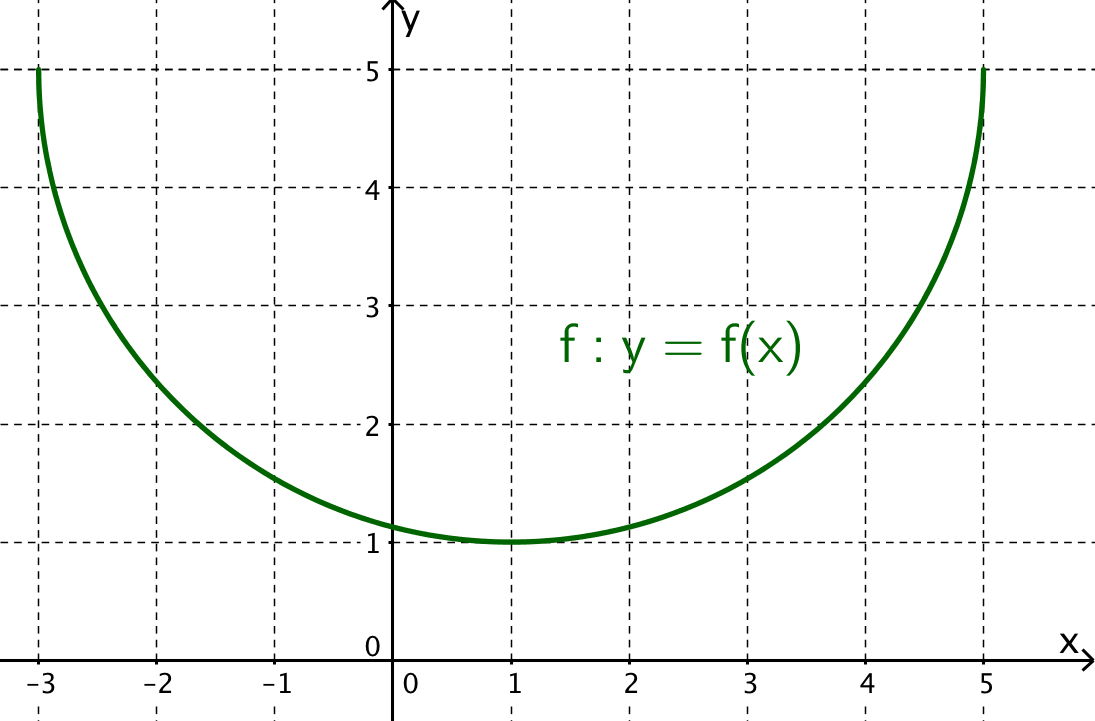
Welche der drei Aussagen über die gezeichnete Funktion f stimmt?
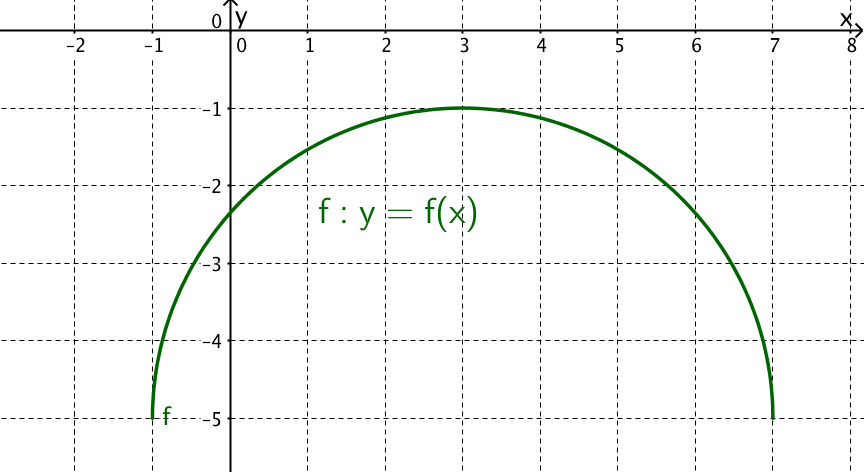
Welche der Aussagen bezüglich der gezeichneten Funktion f stimmt?
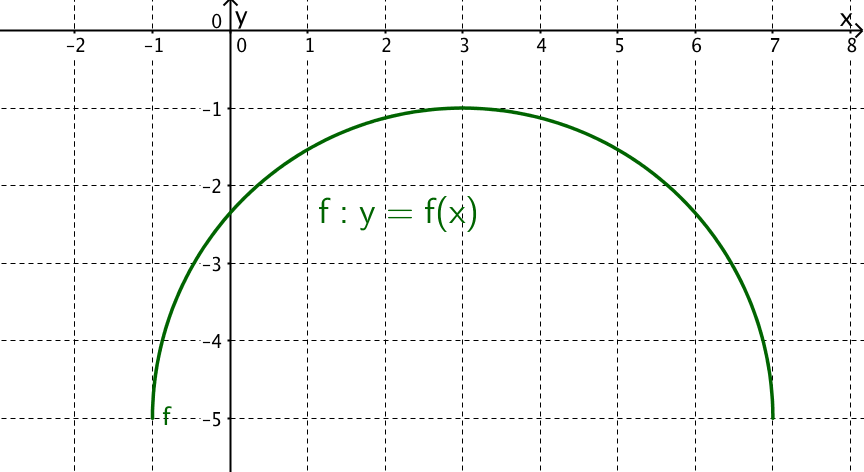
Welche der drei Aussagen über den Stegungswert stimmt?
- 2
Vom Schätzen zum Konstruieren und Berechnen von Steigungen
Wie man die Steigung einer Funktion in einem bestimmten Punkt ermittelt, hängt davon ab, welche Informationen man über die Funktion hat. Man kann Steigungen schätzen, unter Umständen konstruieren, vor allem aber auch berechnen. Wenn man eine Steigung berechnet, dann sagt man, man hat die Funktion "differenziert".
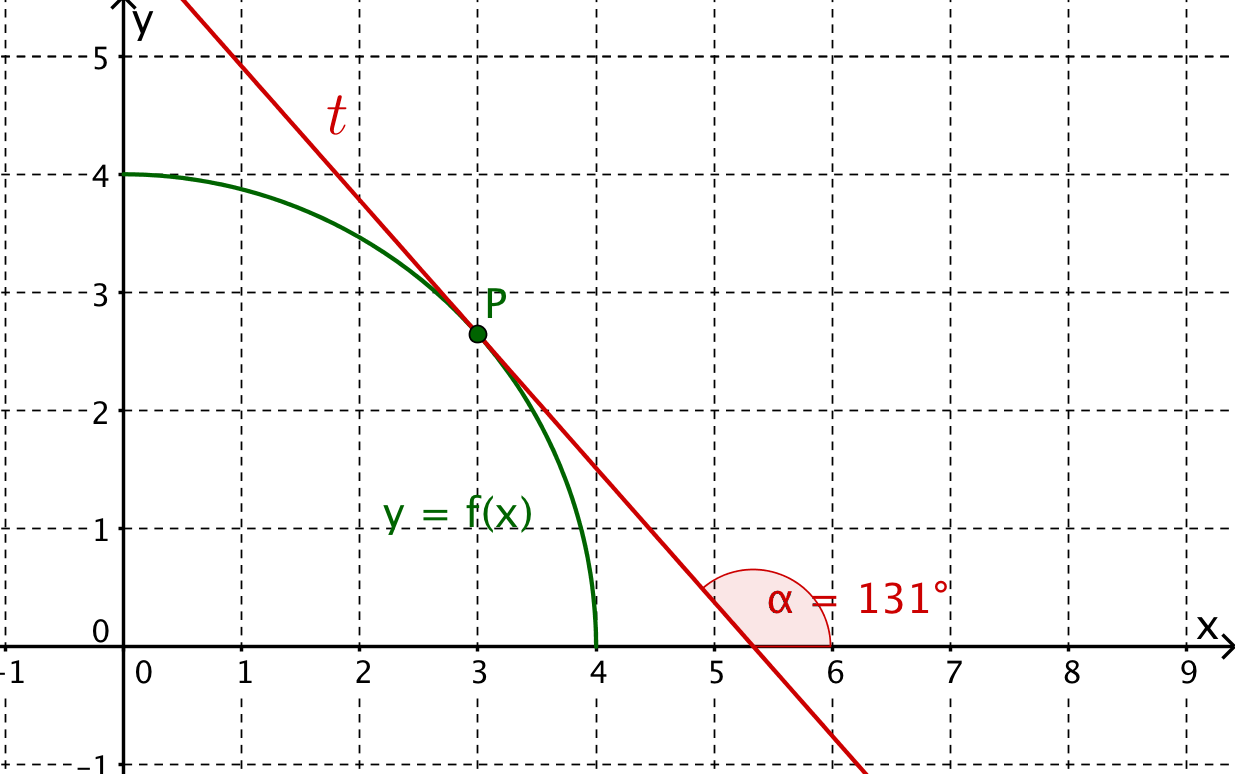
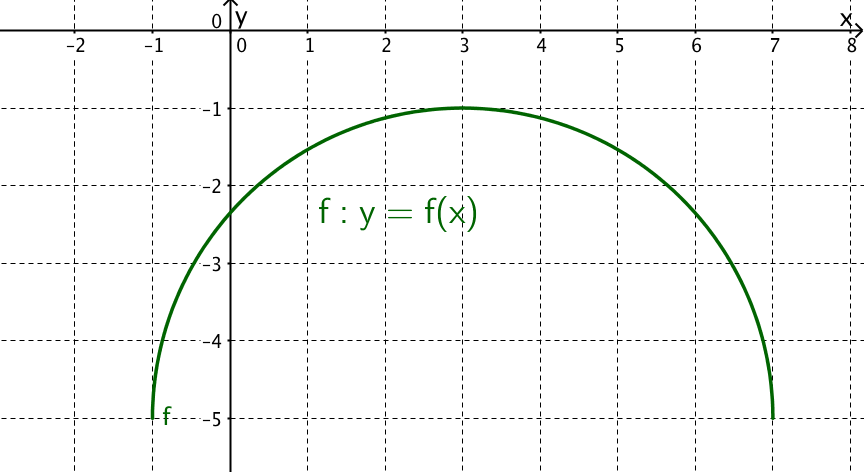
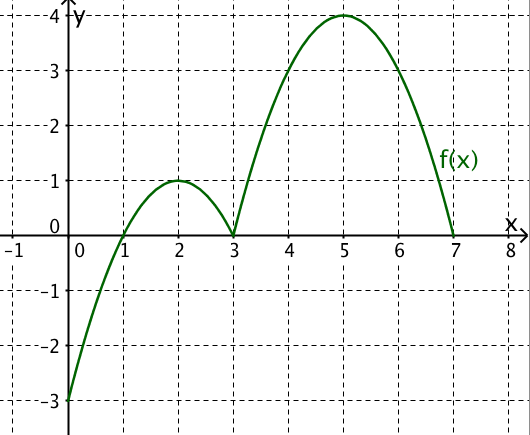
Von der Funktion ist lediglich der Graph gegeben. Schätze die Steigung im Punkt P(3|f(3)).
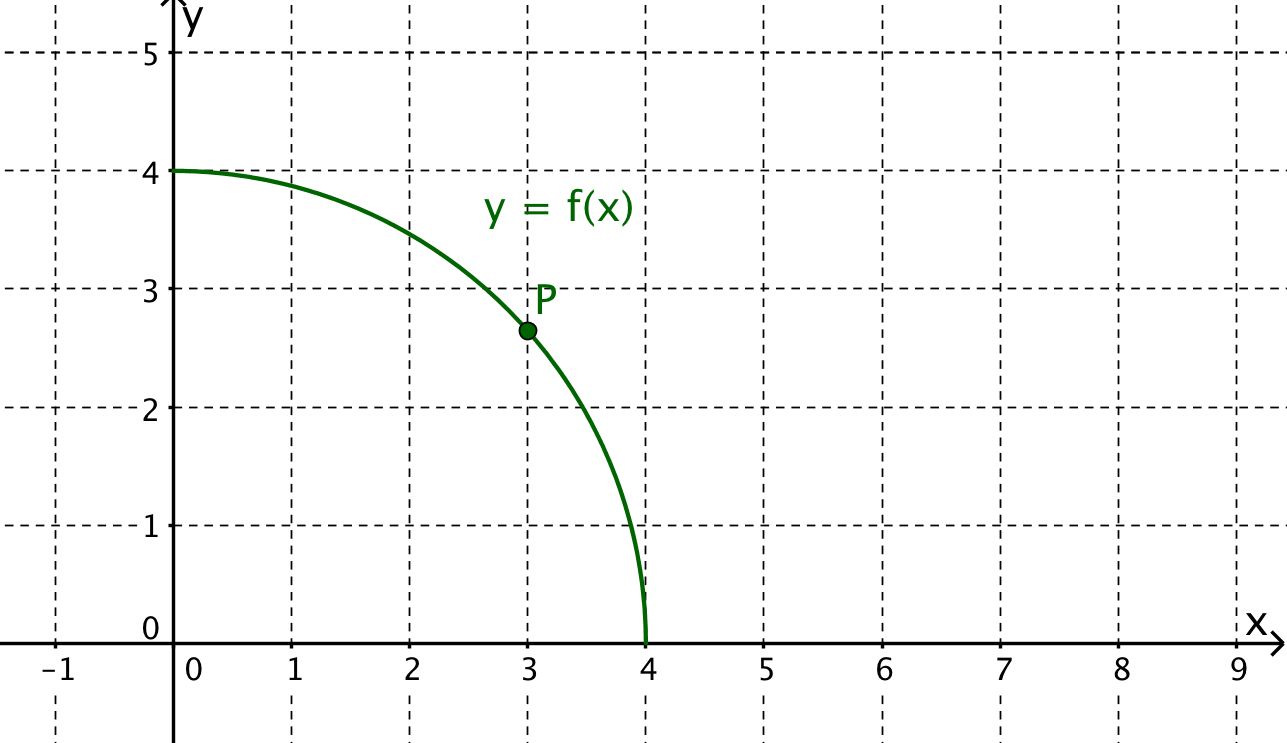
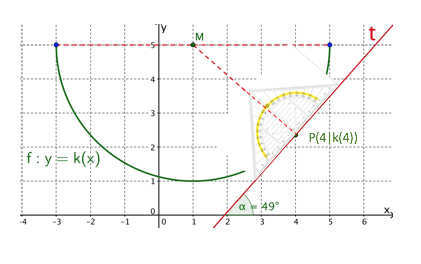
Von der Funktion ist bekannt, dass es sich um eine Halbkreislinie handelt. Konstruiere die Tangente im Punkt und bestimme so den Steigungswert der Funktion k im Punkt .
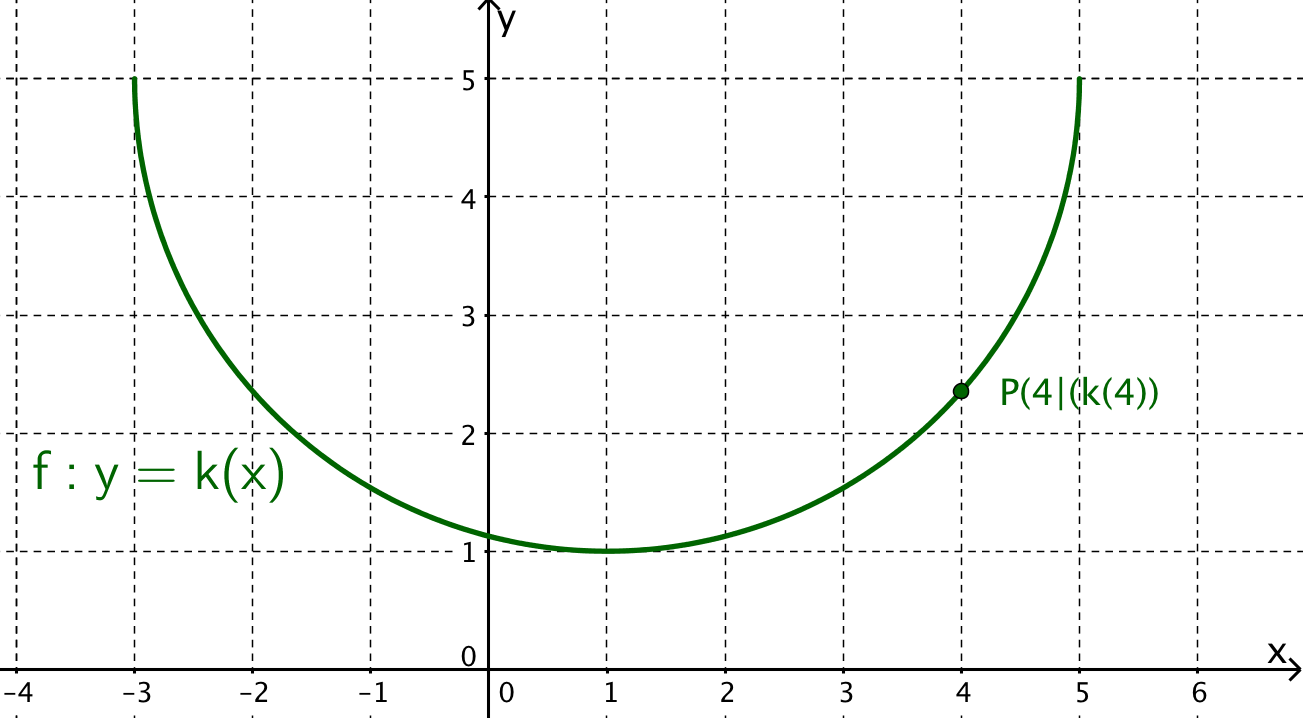
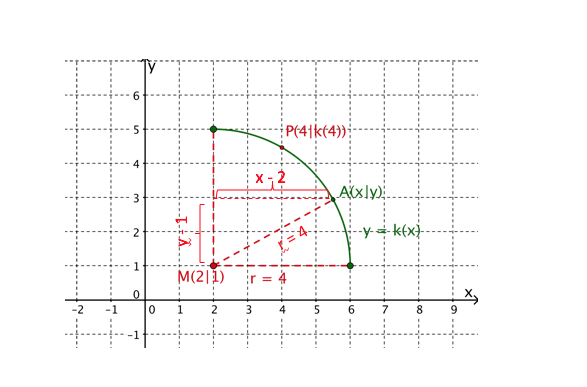
Berechne für den gegebenen Graphen die Steigung .
Es ist bekannt, dass es sich bei dem Graphen um einen Viertelkreis handelt.
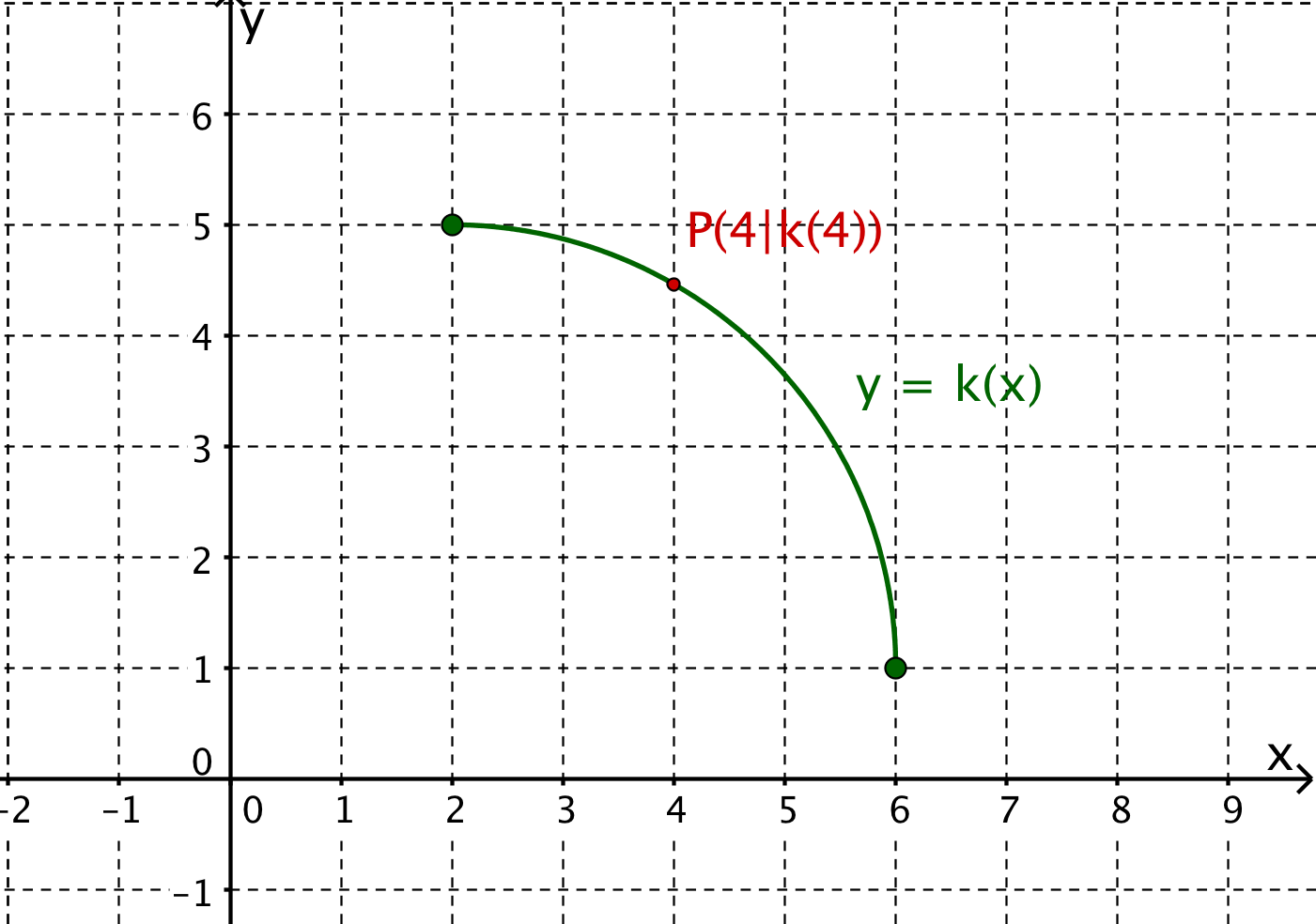
- 3
Betrachte den gegebenen Graphen der Funktion und entscheide, welche der nachfolgenden Aussagen über die Differenzierbarkeit von zutrifft.
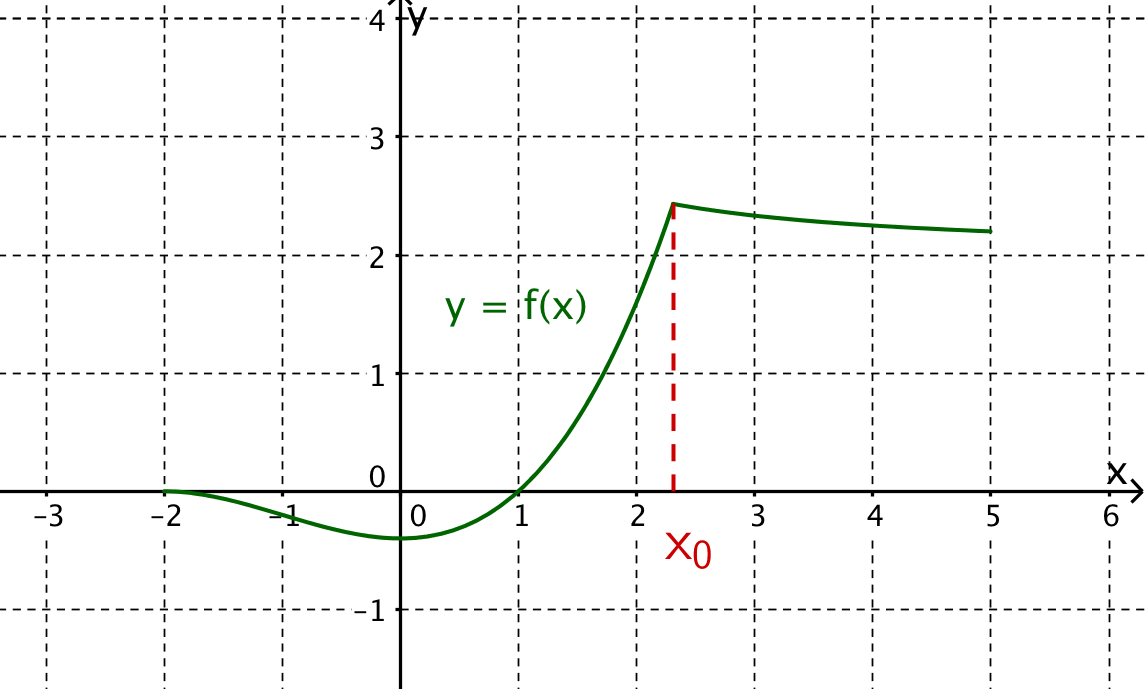
- 4
Achtung Fallen!
Unterscheide bei Funktionswertbetrachtungen eine Angabe von und für Grenzwertberechnungen die Angabe von .
(Nicht nur Anfänger fallen darauf ein.)
Lies aus dem gegebenen Graphen der Funktion so weit möglich folgende Werte ab:
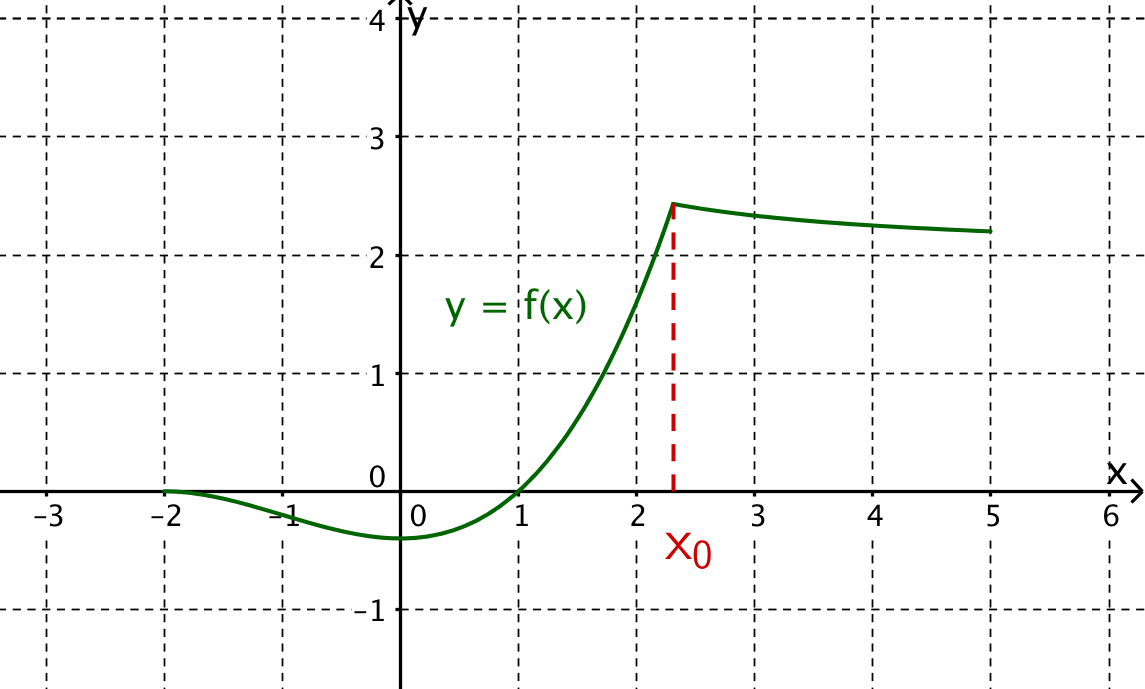
Lies aus dem gegebenen Graphen der Funktion folgende Werte ab:
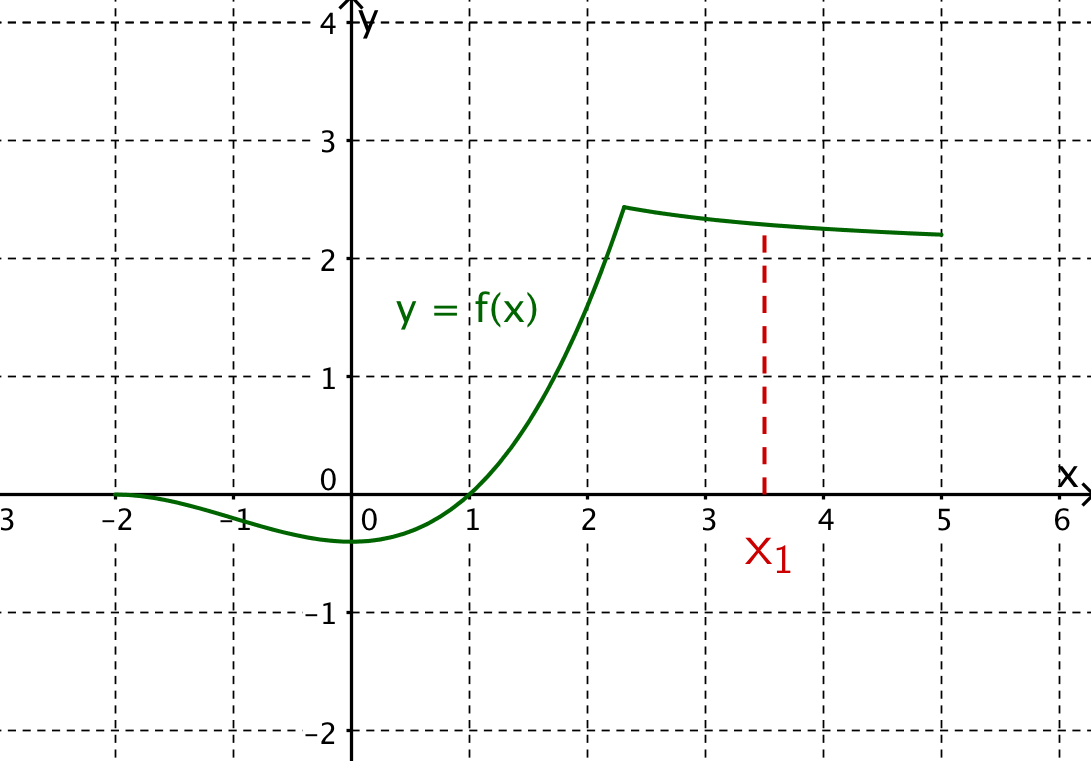
- 5
Entscheide, welche Feststellung auf die gezeichnete Funktion zutrifft.
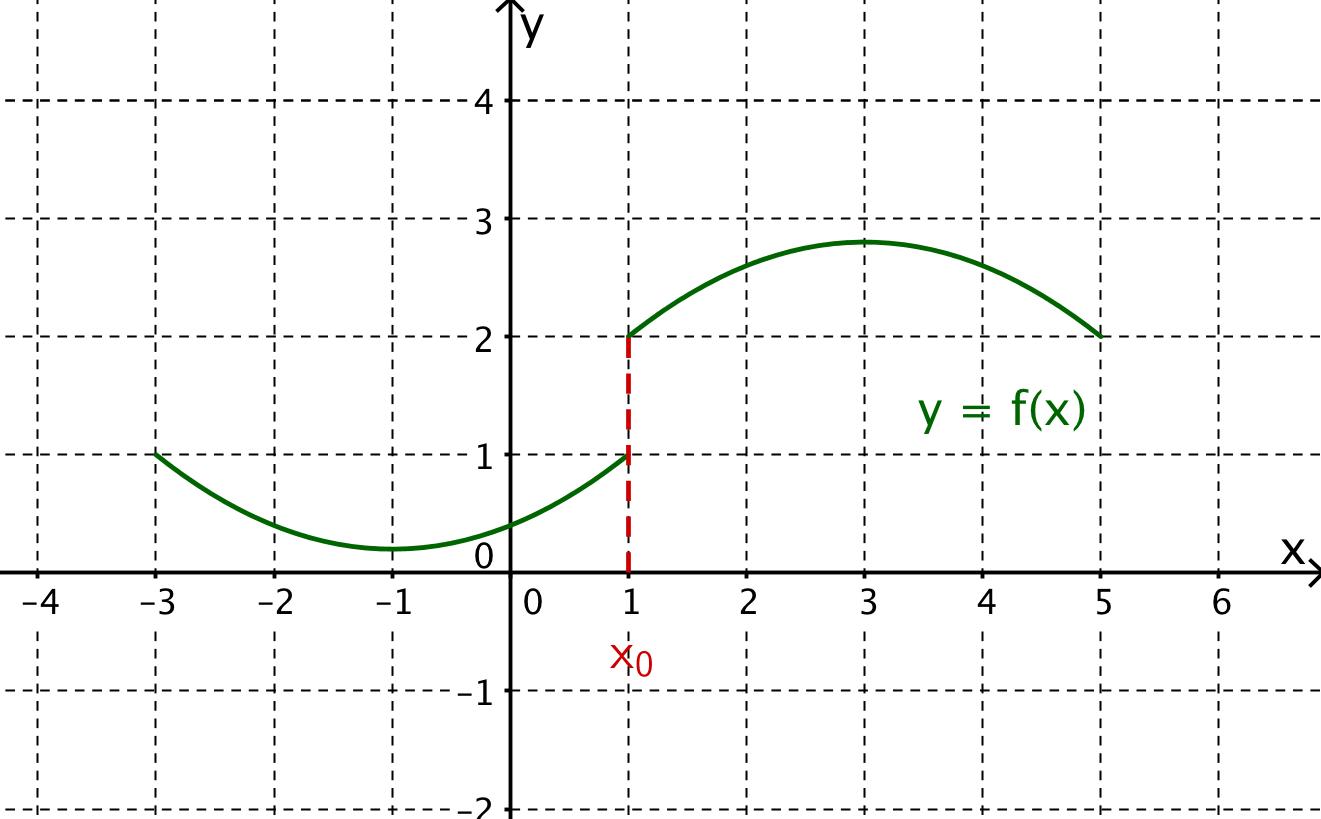
- 6
Graphisches Differenzieren einer linearen Funktion
Die lineare Funktion soll graphisch differenziert werden.
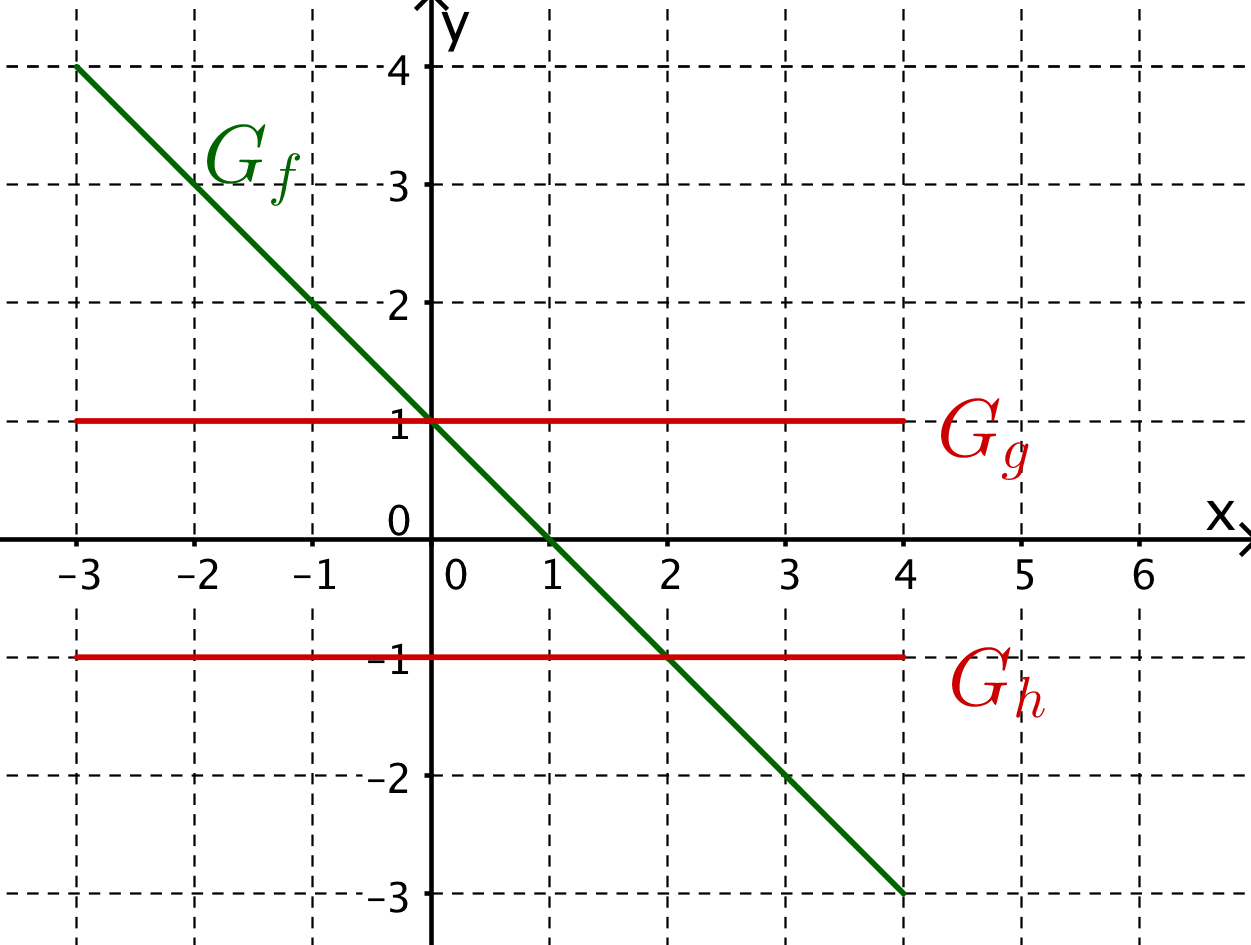
Betrachte die gegebenen Graphen und entscheide, was zutrifft.
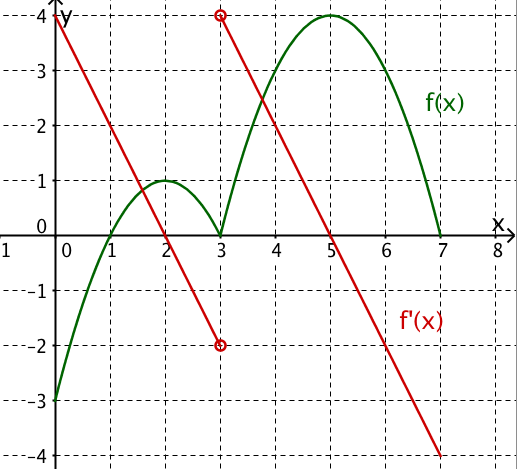
Graphisches Differenzieren einer ganzrationalen Funktion 2. Grades
Die quadratische Funktion p soll graphisch differenziert werden.
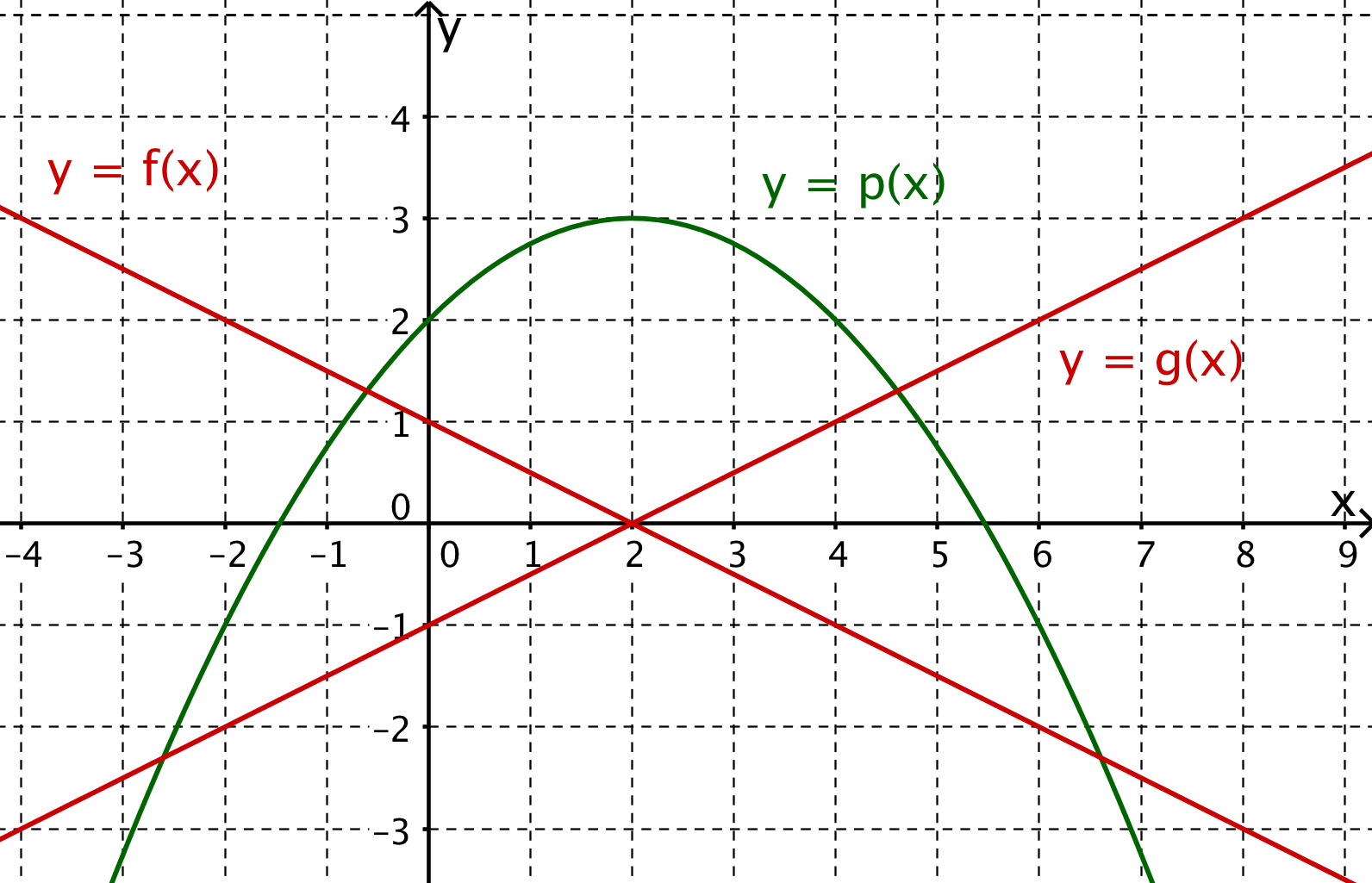
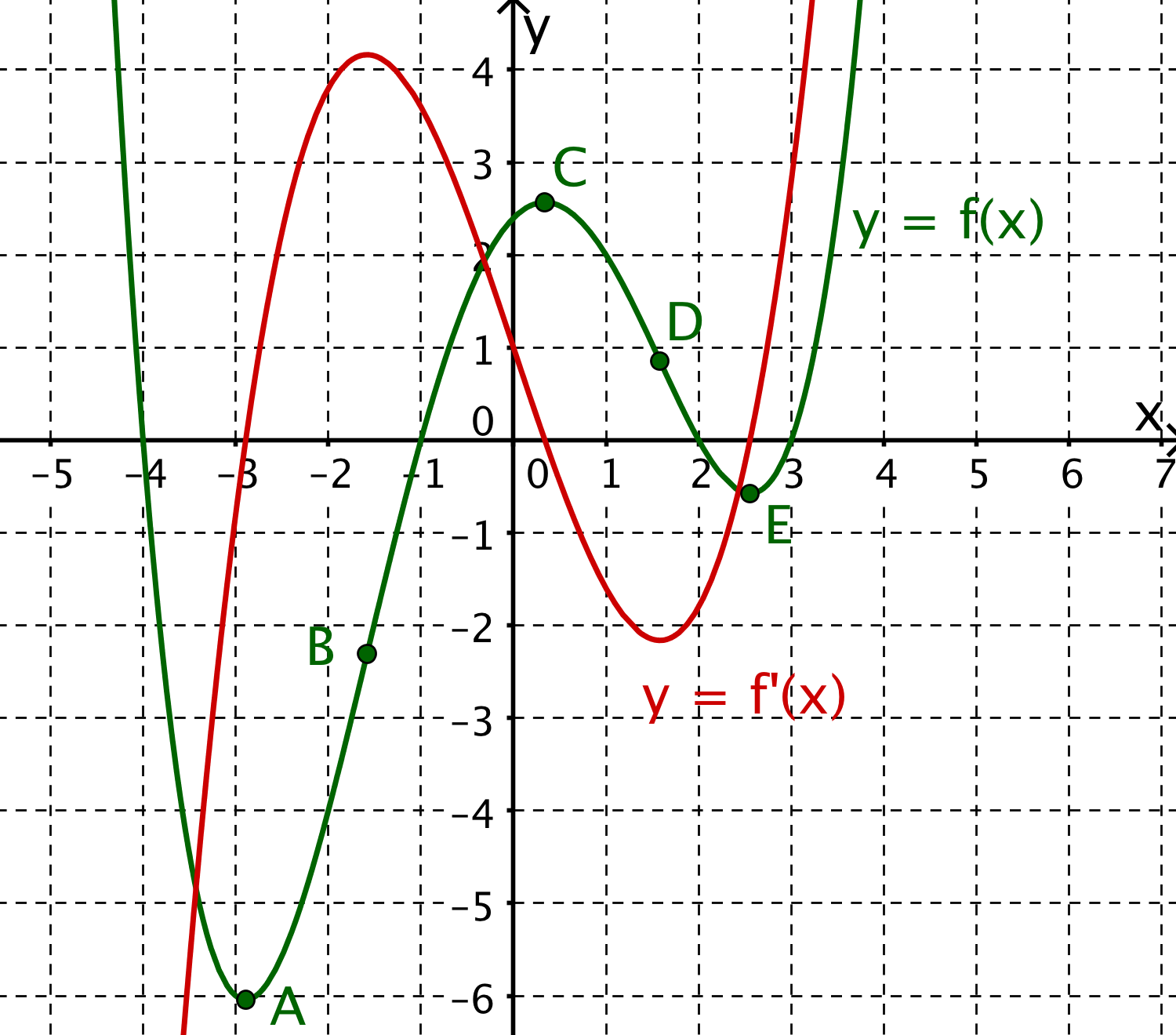
Entscheide, welche der beiden Funktionen oder die Ableitungsfunktion von p ist.
Graphisches Differenzieren einer ganzrationalen Funktion höheren Grades
Fertige durch graphisches Differenzieren eine Skizze der Ableitungsfunktion der nachfolgenden ganzrationalen Funktion 4. Grades.
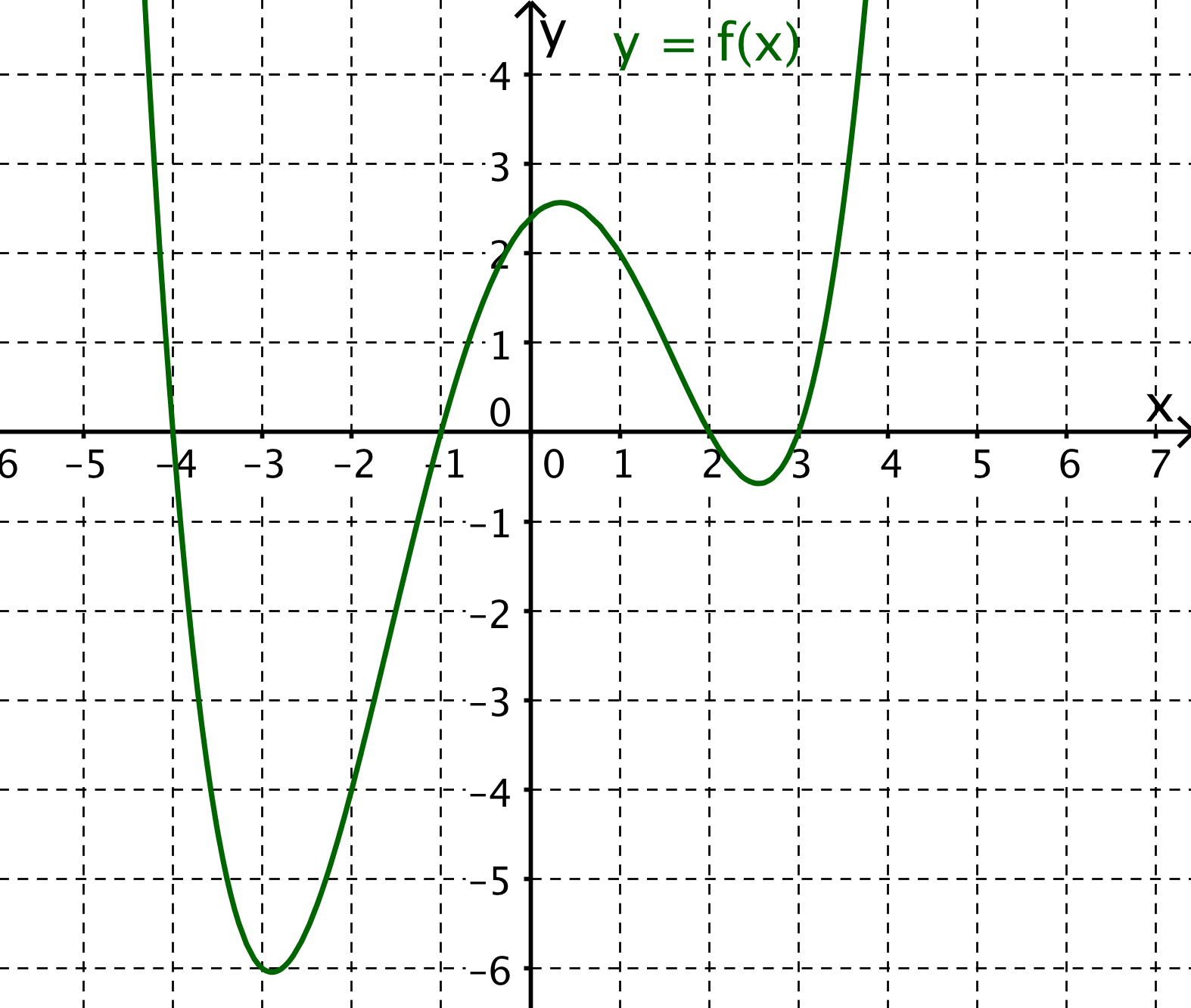
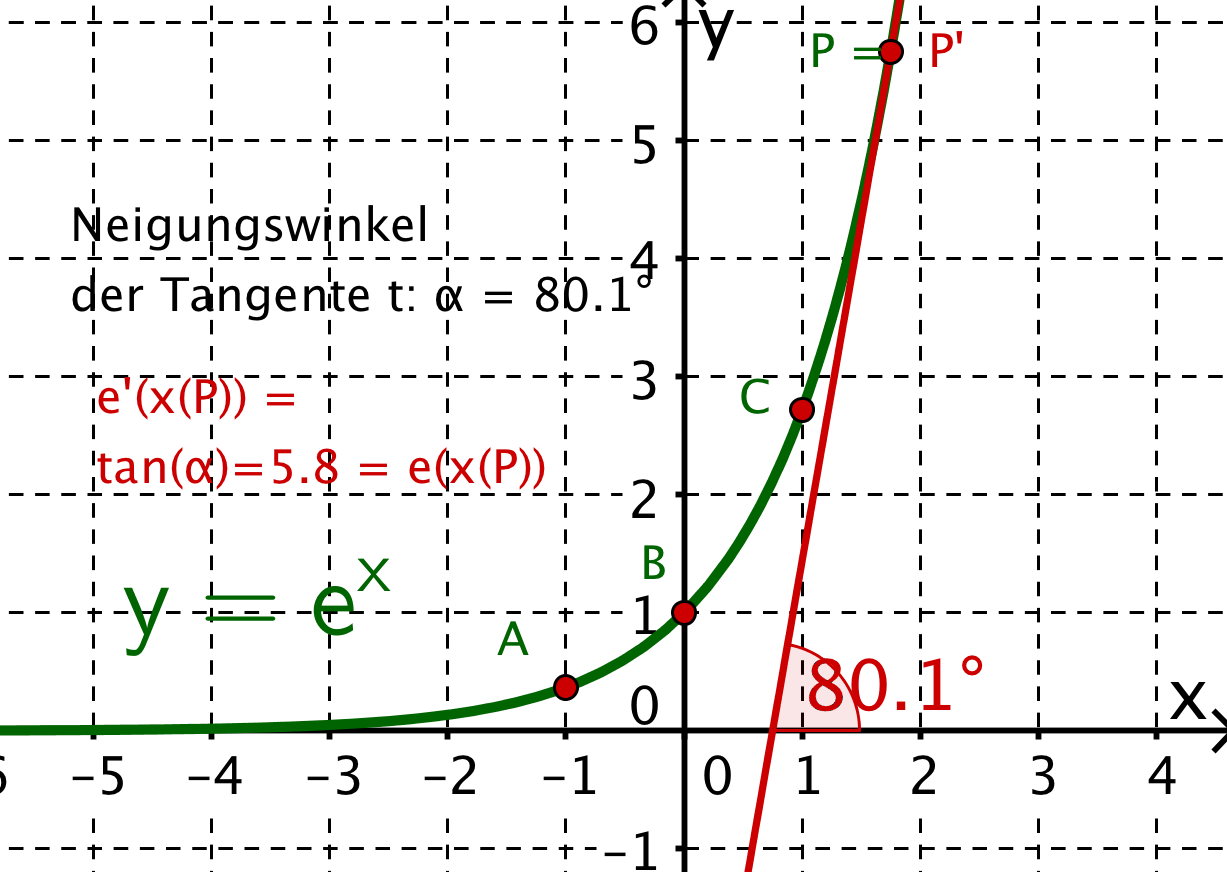
Graphisches Differenzieren der e-Funktion
Die e-Funktion ist für viele Anwendungsgebiete der Mathematik eine der wichtigsten Funktionen.
Graphisch gesehen ist sie aber eher eine besonders "langweilige" Funktion: ohne Nullstellen, ohne lokale Extrema und ohne Wendepunkte - einfach nur steigend.
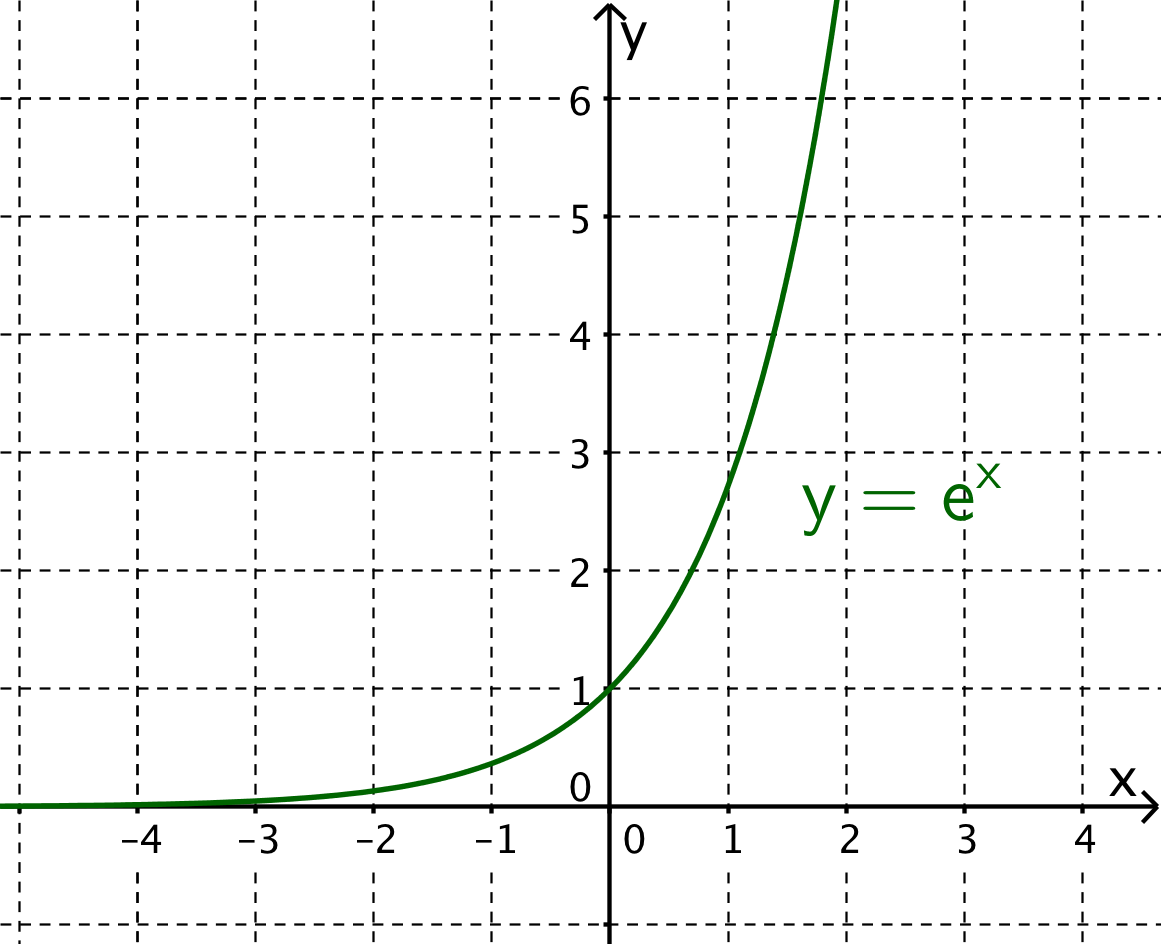
Welche überraschende Besonderheit der e-Funktion entdeckst du aber, wenn du dich um eine möglichst genaue Skizze beim graphischen Differenzieren der e-Funktion bemühst?
Graphisches Differenzieren einer abschnittsweise definierten Funktion
Die folgende Funktion ist graphisch zu differenzieren.
Klicke die richtige Lösung an!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?