Aufgaben zum Monotonieverhalten
Teste mit diesen Aufgaben dein Wissen zum Monotonieverhalten von Graphen!
- 1
Bestimme das Monotonieverhalten der nachfolgenden Funktionen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonieverhalten berechnen
Variante 1
↓ Die Funktion ist ein Polynom und daher (beliebig oft) differenzierbar. Du kannst daher die erste Ableitung von berechnen um das Monotonieverhalten zu bestimmen.
↓ Die erste Ableitung ist also erneut ein Polynom.
Berechne nun die Nullstellen von .
↓ Setze die Funktionsgleichung von ein.
Teile beide Seiten der Gleichung durch .
Die linke Gleichungsseite ist durch ein Polynom zweiten Grades gegeben. Es hat also höchstens zwei reelle Nullstellen. Durch Anwendung der p-q-Formel erhältst du
Dies sind zwei reelle Nullstellen und daher genau die Lösungen der Gleichung.
Da nur diese Nullstellen hat und als Polynom insbesondere reellwertig, auf ganz definiert und stetig ist, kannst du den Zwischenwertsatz verwenden.
Betrachte die Intervalle
,
die zwischen den Nullstellen von liegen.
Wähle beispielsweise
Setze diese in ein.
Somit gilt
womit auf und streng monoton wächst, sowie auf streng monoton fällt.
Variante 2
Bildung der ersten Ableitung:
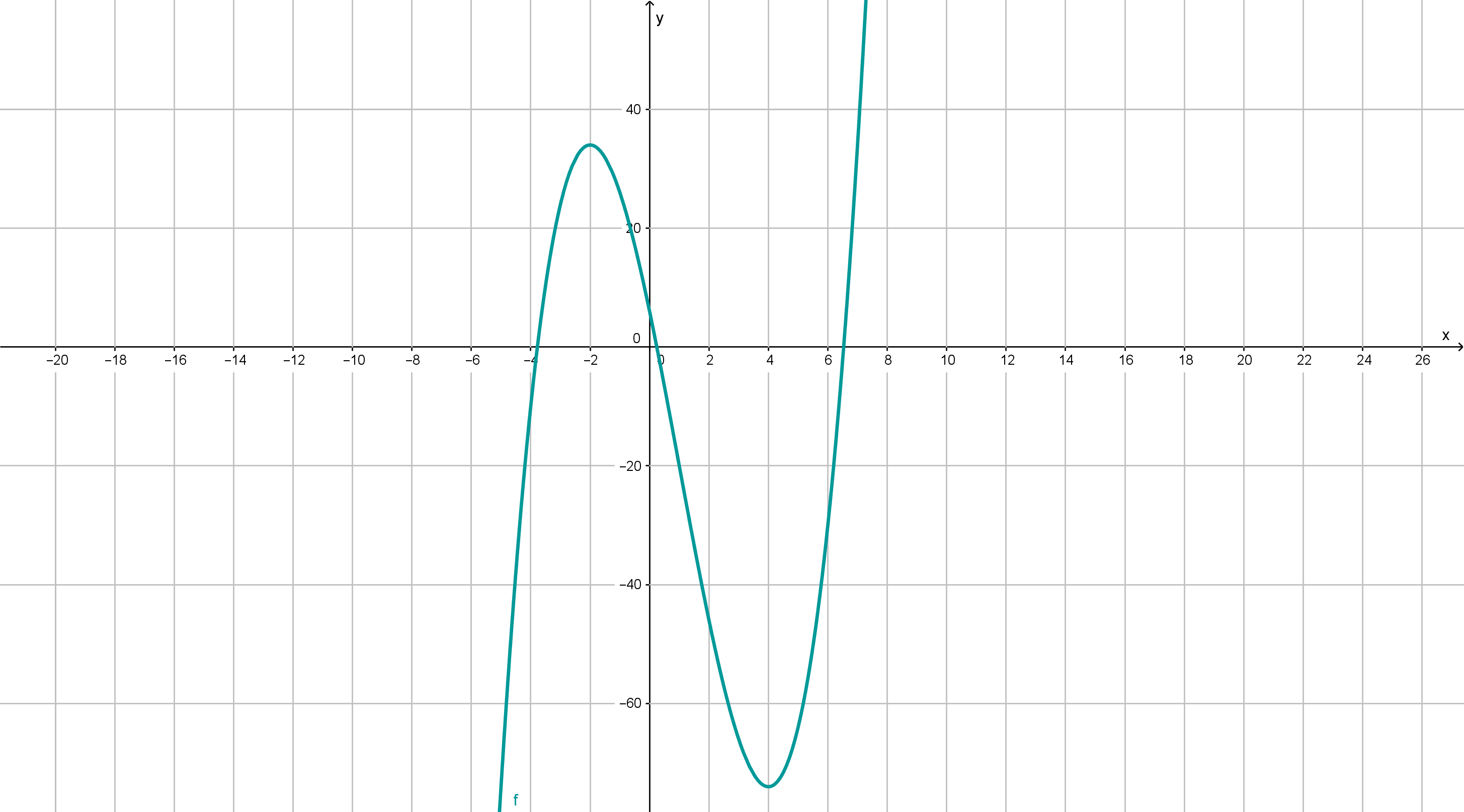
Der Graph der vorzeichengleichen Funktion ist eine nach oben geöffnete Parabel mit den genannten Nullstellen.Links von der Nullstelle
liegt der Graph oberhalb der x-Achse. Das bedeutet, dass f' in diesem Bereich positiv ist und der Graph von f im Intervall
wachsend und im Intervall
liegt der Graph von f' unterhalb der x-Achse und somit ist f' dort negativ und f fällt.Rechts von x=4 wächst die Funktion dann wieder.Somit liegt an der Stelle
ein Maximum und an der Stelle
ein Minimum.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonieverhalten berechnen
Die Funktion ist ein Polynom und daher (beliebig oft) differenzierbar. Du kannst also die erste Ableitung von berechnen, um das Monotonieverhalten zu bestimmen.
Die erste Ableitung ist also erneut ein Polynom.
Berechne nun die Nullstellen von .
Setze die Funktionsgleichung von ein.
Teile beide Seiten der Gleichung durch .
Die linke Gleichungsseite ist durch ein Polynom dritten Grades gegeben. Es hat also höchstens drei reelle Nullstellen.
Die linke Seite der Gleichung ist genau dann gleich , wenn mindestens einer der beiden Faktoren gleich ist. Dadurch kannst du sofort die Nullstelle bei ablesen.
Im zweiten Fall könnte gleich sein.
Durch Anwendung der Mitternachtsformel erhältst du
Somit sind alle drei Nullstellen von reell.
Da nur diese Nullstellen hat und als Polynom insbesondere reellwertig, auf ganz definiert und stetig ist, kannst du den Zwischenwertsatz verwenden.
Betrachte die Intervalle
,
die zwischen den Nullstellen von liegen.
Wähle beispielsweise
Setze diese in ein.
Somit gilt
womit auf und streng monoton wächst, sowie auf und streng monoton fällt.
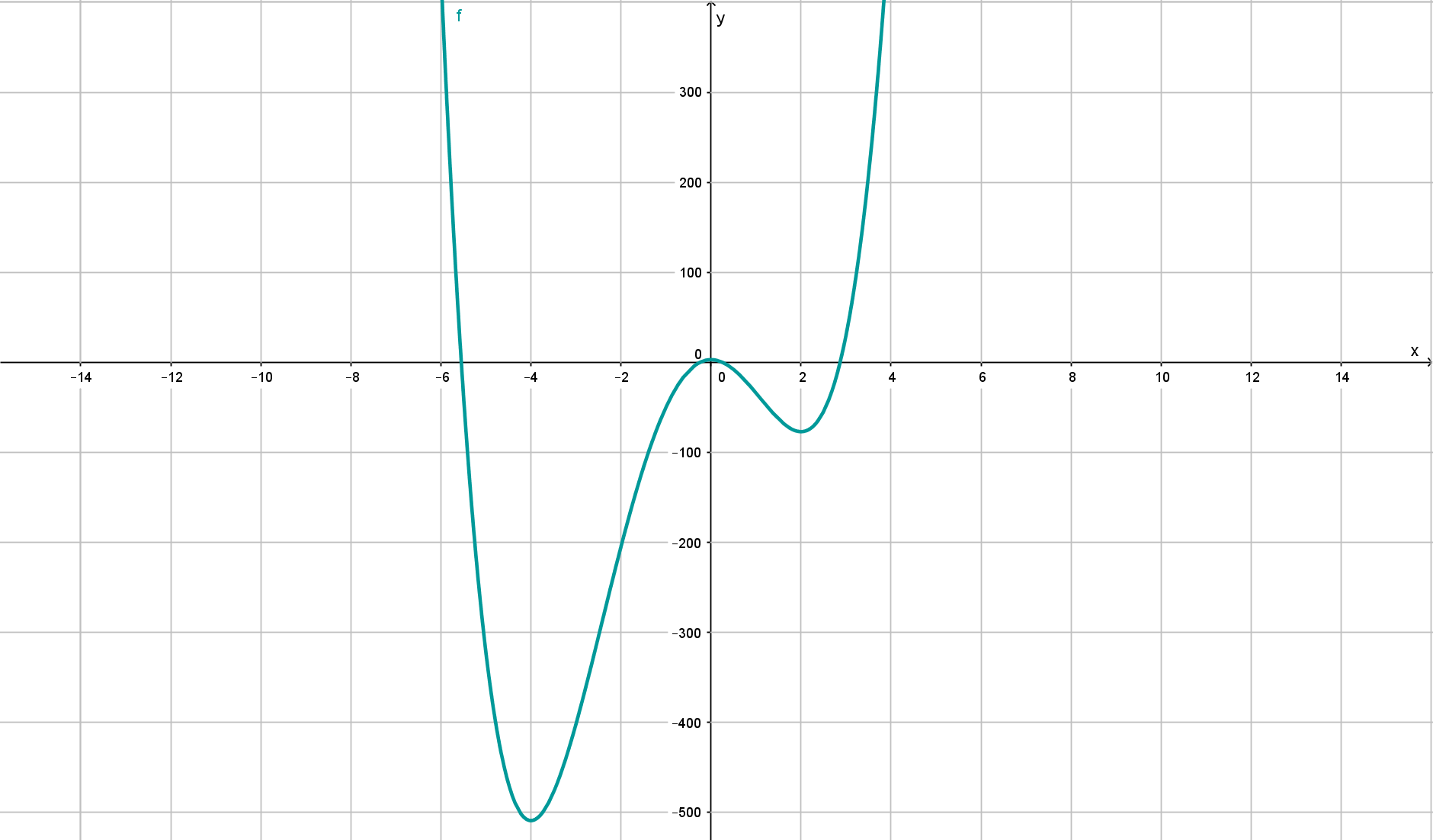
Anmerkung zum obigen Bild
In diesem Bild, sieht es so aus, als ob die Funktion durch den Wert geht. Das ist aber hier nur der Fall, weil zu weit reingezoomt wurde, damit man die gesamte Funktion, insbesondere das Minimum bei sieht ;) Daher folgt nochmal ein Bild von der Funktion ohne den unteren Part mit dem Minimum bei :
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonieverhalten berechnen
Die Funktion ist ein Quotient zweier Polyonme, du kannst daher die erste Ableitung mit der Quotientenregel berechnen um das Monotonieverhalten zu bestimmen.
Nullstelle von (also Extrema von ) berechnen:
Die Nullstellen einer gebrochen rationalen Funktion sind gleichzeitig die Nullstellen des Zählers.
Vereinfache diesen Ausdruck:
Nun kann man ganz leicht die Nullstellen der 1. Ableitung (die Extrema von ) ablesen.
Hier wird nun der Weg mit der Monotonietabelle gewählt, da die 2. Ableitung relativ kompliziert ist. Man muss allerdings bei der Monotonietabelle die Polstellen der Funktion beachten.
und
Berechnen der Polstelle . Suche also die Nullstellen des Nenners von . (Übrigens haben und immer dieselben Polstellen.)
Faktorisiere nun die 1. Ableitung.
Erstelle eine Vorzeichentabelle.
Achtung: Polstelle nicht vergessen!
Nun kann man aus der Vorzeichentabelle das Monotonieverhalten ganz einfach ablesen. Steht in der letzten Zeile ein Minus ist die Funktion in diesem Bereich streng monoton fallend, steht dort ein Plus ist die Funktion streng monoton steigend.
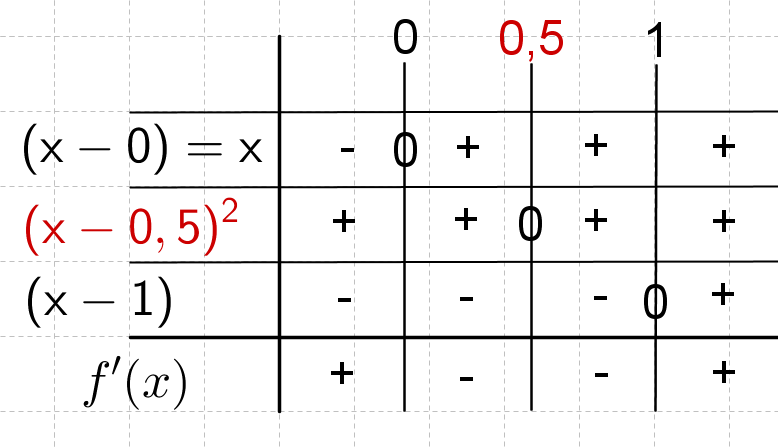
: ist streng monoton steigend
: ist streng monoton fallend
: ist streng monoton fallend
ist streng monoton steigend
Achtung:
Man darf die beiden Intervalle und nicht zu einem Intervall zusammenlegen, da die Funktion und damit die Monotonie an dem Wert nicht definiert ist.
Hast du eine Frage oder Feedback?
- 2
Interaktive Aufgaben zum Steigungsverhalten auf KMap ..
- 3
Bestimme rechnerisch die lokalen Extrema der Funktion mit der Gleichung:
Bilde die ersten beiden Ableitungen:
Damit ein lokales Extremum existiert, muss die notwendige Bedingung erfüllt sein:
Damit gibt es zwei Kandidaten für lokale Extrema. Falls die zweite Ableitung bei einem gefundenen Kandidaten ungleich Null ist, ist die hinreichende Bedingung erfüllt und es ist nachgewiesen, dass es sich um lokale Extremstellen handelt:
Das ist echt größer als Null. Damit ist eine lokale Extremstelle. Da die zweite Ableitung größer Null ist, muss hier ein Minimum vorliegen. Um den Extrempunkt angeben zu können muss man nun noch in die Funktionsgleichung einsetzen:
Also ist ein lokales Mininmum gefunden:
Nun noch für das gleiche Vorgehen:
Das ist echt kleiner als Null. Damit ist eine lokale Extremstelle. Da die zweite Ableitung kleiner Null ist, muss hier ein Maximum vorliegen. Um den Extrempunkt angeben zu können muss man nun noch in die Funktionsgleichung einsetzen:
Also ist ein lokales Maximum gefunden:
- 4
Gegeben ist die Funktion mit der Gleichung
Untersuche die Funktion rechnerisch auf lokale Extrema.
Um auf lokale Extrema zu untersuchen benötigt man die ersten beiden Ableitungen:
Damit ein lokales Extremum existiert, muss die notwendige Bedingung erfüllt sein:
Damit gibt es zwei Kandidaten für lokale Extrema. Falls die zweite Ableitung bei einem gefundenen Kandidaten ungleich Null ist, ist die hinreichende Bedingung erfüllt und es ist nachgewiesen, dass es sich um lokale Extremstellen handelt:
Das ist echt kleiner als Null. Damit ist eine lokale Extremstelle. Da die zweite Ableitung kleiner Null ist, muss hier ein Maximum vorliegen. Um den Extrempunkt angeben zu können muss man nun noch in die Funktionsgleichung einsetzen:
Also ist ein lokales Maximum gefunden:
Für das gleiche Vorgehen:
Das ist echt größer als Null. Damit ist eine lokale Extremstelle. Da die zweite Ableitung größer Null ist, muss hier ein Minimum vorliegen. Um den Extrempunkt angeben zu können muss man nun noch in die Funktionsgleichung einsetzen:
Also ist ein lokales Minimum gefunden:
Für das gleiche Vorgehen:
Das ist echt größer als Null. Damit ist eine lokale Extremstelle. Da die zweite Ableitung größer Null ist, muss hier ein Minimum vorliegen. Um den Extrempunkt angeben zu können muss man nun noch in die Funktionsgleichung einsetzen:
Also ist ein weiteres lokales Minimum gefunden:
Hast du eine Frage oder Feedback?
Untersuche, ob die unter a) gefundenen lokalen Extrema auch globale Extrema sind.
Da , kann kein globales Maximum sein.
Da , kann bei kein globales Minimum sein.
Nun ist nur noch zu prüfen, ob bei ein globales Minimum vorliegt. Wenn bei ein globales Minimum wäre, würde gelten für alle aus dem Definitionsbereich. Wir nehmen mal an, dass dies nicht so ist. Dann müsste es geben, für die gilt:
Durch folgende Überlegung kann man aber nachweisen, dass es keine x-Werte kleiner als geben kann:
und
Die Funktion ist wie jede ganzrationale Funktion stetig.
Die Funktion kann nur drei Extrema besitzen (siehe notwendige Bedingung aus Aufgabe a)).
Sollte es noch Werte kleiner als geben, müsste die Funktion aber noch ein Minimum haben da sie stetig ist und das angegebenen Verhalten im Unendlichen hat. Schließlich muss sie wieder "hinauf". Bei muss demnach ein globales Minimum vorliegen.
Hast du eine Frage oder Feedback?
- 5
Gegeben ist die Funktion mit und Graph . Bestimme die maximalen Monotonieintervalle der Funktion f sowohl mit einer Monotonietabelle als auch mit mit einer Skizze des Graphen der Ableitungsfunktion .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Stellen mit waagerechten Tangenten ermitteln
Da sich bei ganzrationalen Funktionen das Monotonieverhalten nur an Stellen mit waagerechten Tangenten (Steigung m=0) ändern kann, suchst du die Nullstellen der Ableitung.
Bilde die Ableitung:
Setzte die Ableitung mit 0 gleich und löse die Gleichung:
↓ Klammere 4x aus (du kannst auch nur x ausklammern)
Aufgrund des Satzes vom Nullprodukt kannst du die Faktoren getrennt betrachten, um die Nullstellen zu bestimmen.
Die erste Nullstelle ist direkt . Die zweite erhältst du mithilfe der Mitternachtsformel aus
Mitternachtsformel: liefert und .
Lösung mithilfe einer Skizze des Graphen der Ableitung
Es handelt sich lediglich um eine Skizze, deshalb brauchst du nur:
Die Nullstellen von f' und ihre Vielfachheit (alle Nullstellen sind hier mit Vielfachheit 1)
Den Grad und Leitkoeffizienten von f' für den Globalverlauf.
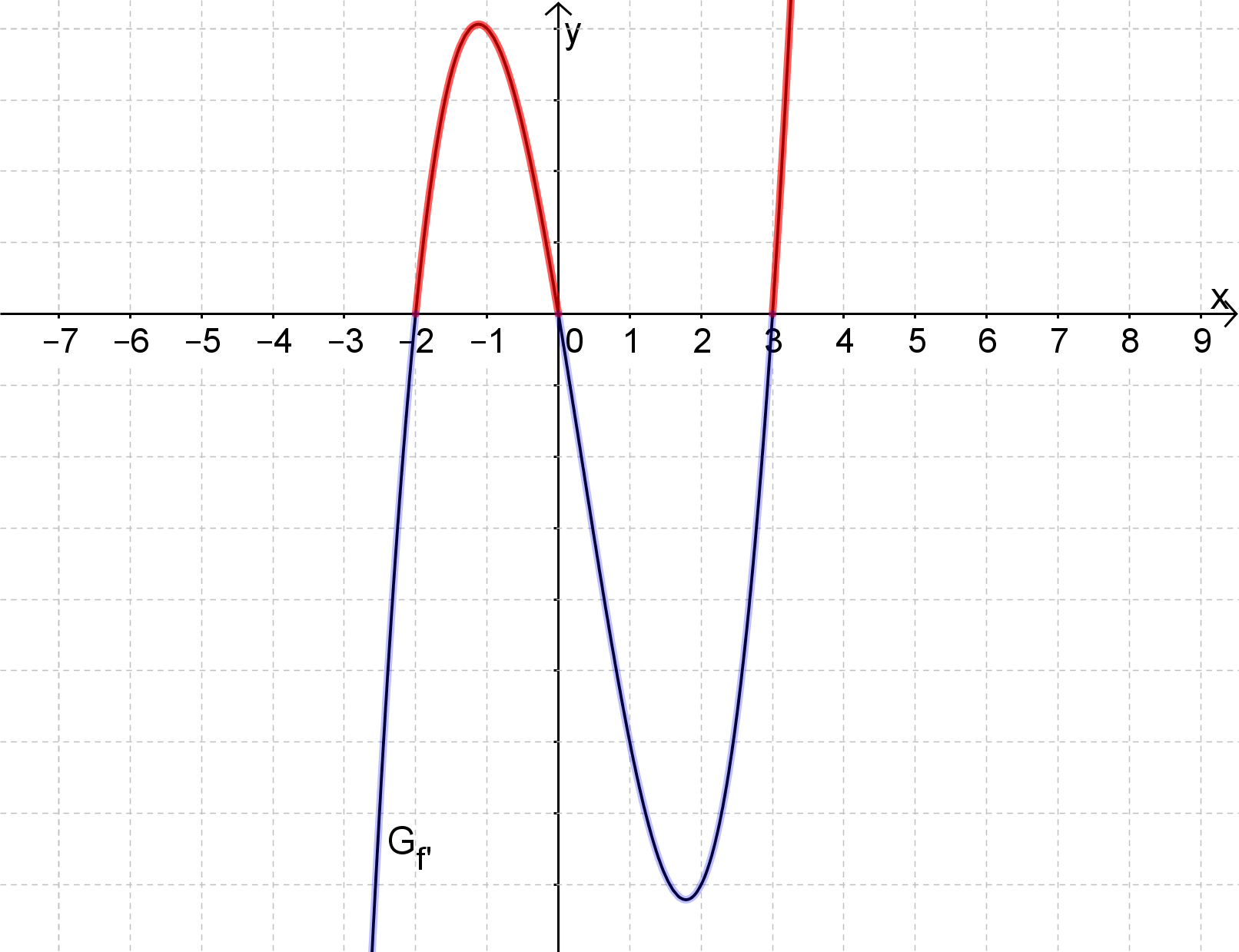
Trage zunächst die Nullstellen an. Es sind alles einfache, also schneidende Nullstellen.
Der Grad ist ungerade (3) und der Leitkoeffizent positiv, der Graph kommt also von unten.
Jetzt musst du nur noch entsprechend der Vielfachheiten die x-Achse schneiden.
Der Graph der Ableitungsfunktion zeigt für jeden x-Wert die Steigung, die der zugehörige Punkt von an dieser Stelle hat. Steigt der Graph in einem Bereich, so ist der Wert der Steigung positiv und verläuft oberhalb der x-Achse. Umgekehrt verläuft unterhalb der x-Achse, wenn fällt.
Der Graph ist also streng monoton steigend für und streng monoton fallend für .
(Nicht gefragt: Bei und liegen Tiefpunkte, bei ein Hochpunkt)
Alternative Lösung über Monotonietabelle
Wenn du nicht zeichnen möchtest, kannst du das gleiche schriftlich mit einer Monotonietabelle machen.
Die Spalten beschreiben die Nullstellen der Ableitungsfunktion und die Bereiche zwischen diesen
Die mittlere Zeile zeigt das Vorzeichen von f' in diesem Bereich an
Die unterste Zeile enthält direkt das Monotonieverhalten
x
x<
-2
<x<
0
<x<
3
<x
-
0
+
0
-
0
+
(smf)
TIP
(sms)
HOP
(smf)
TIP
(sms)
Auf die Inhalte der 2. Zeile kommst du entweder durch ähnliche Überlegungen wie schon bei der Skizze oder du setzt - im Kopf oder im Taschenrechner - einen Beispielwert aus diesem Bereich ein.
Die Inhalte der 3. Zeile folgen aus denen der 2. Zeile, wobei du zuerst die Pfeile einzeichnest und dann die Angabe zu Hochpunkt, Tiefpunkt oder Terrasenpunkt ergänzt.
Für beide Methoden musst du zunächst die Ableitung bilden und die Nullstellen der Ableitung berechnen (denn nur an Stellen mit waagerechten Tangenten kann sein Monotonieverhalten ändern).
Achte bei beiden Methoden darauf, dass du Berechnungen/Überlegungen für f' anstellst, um Aussagen über den Verlauf von zu machen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

