Abstand eines Punktes zu einer Geraden berechnen (Analytische Geometrie)

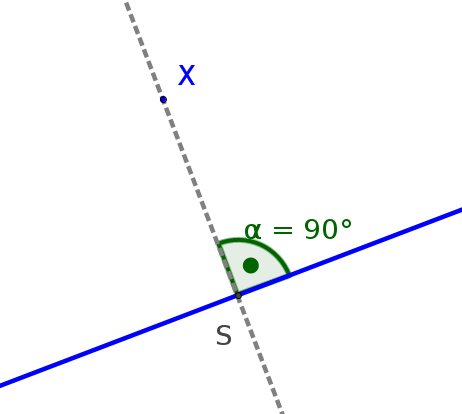
Den Abstand eines Punktes $X$ zu einer Geraden bestimmt man, indem man das Lot durch den Punkt $X$ auf die Gerade fällt. Den Schnittpunkt des Lotes und der Geraden bezeichnet man mit $S$ . Die Länge der Strecke $[SX]$ ist somit genau der Abstand vom Punkt $X$ und der Geraden.

Berechnung im 3-dimensionalen Fall

Gegeben sind der Punkt $P(p_1|p_2|p_3)$ und die Gerade $g:\vec X = \vec a + \lambda\cdot \vec b$

Formel zur Berechnung des Abstandes:

\displaystyle d= \frac{|(\vec p - \vec a )\times \vec b|}{|\vec b|}

Beispiel

Berechne den Abstand des Punktes $P(3|2|1)$ von der Geraden $g:\;\vec X=\begin{pmatrix}-3 \\ 4 \\ -1 \end{pmatrix}+\lambda\cdot\begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix}$

Man setzt die Werte in die Formel ein:

$\displaystyle d$	$=$	$\displaystyle \dfrac{\left\|\left(\begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix}-\begin{pmatrix} -3 \\ 4 \\ -1 \end{pmatrix}\right)\times\begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix} \right\|}{\sqrt{(-1)^2+2^2+1^2}}$
	↓	Berechne die Vektordifferenz und die Summe unter der Wurzel.
	$=$	$\displaystyle \dfrac{\left\|\begin{pmatrix} 6 \\ -2 \\ 2 \end{pmatrix}\times\begin{pmatrix} -1 \\ 2 \\ 1 \end{pmatrix}\right\|}{\sqrt6}$
	↓	Berechne das Vektorprodukt.
	$=$	$\displaystyle \dfrac{\left\|\begin{pmatrix} -2-4 \\ -2-6 \\ 12-2\end{pmatrix}\right\|}{\sqrt{6}}$
	↓	Berechne den Betrag des Vektors.
	$=$	$\displaystyle \dfrac{\sqrt{(-6)^2+(-8)^2+10^2}}{\sqrt6}$
	↓	Vereinfache den Zähler.
	$=$	$\displaystyle \dfrac{\sqrt{200}}{\sqrt6}$
	↓	Vereinfache.
	$=$	$\displaystyle \dfrac{10}{\sqrt3}$

Antwort: Der Abstand des Punktes $P(3|2|1)$ zu der Geraden $g$ beträgt $d=\dfrac{10}{\sqrt3}\;\text{LE}$ .

Alternative schrittweise Berechnung mit einer Hilfsebene

Gegeben sind der Punkt $P(p_1|p_2|p_3)$ und die Gerade $g:\vec X = \vec a + \lambda\cdot \vec b$

Folgende Schritte werden verwendet, um den Abstand zu bestimmen:

1. Schritt:

Man erstellt eine Hilfsebene in Normalform, die durch den Punkt $P(p_1|p_2|p_3)$ geht und orthogonal zum Richtungsvektor $\vec{b}$ ist.

2. Schritt:

Wenn man die Ebene in Koordinatenform haben möchte, um die danach folgende Rechnung zu vereinfachen, wandelt man sie in diese um.

3. Schritt:

Nun bestimmt man den Schnittpunkt der Hilfsebene $E$ mit der Geraden $g$ . Das ist das Lot des Punktes $P$ auf die Gerade $g$ . Man fängt damit an, die beiden Gleichungen zu kombinieren, um $\lambda$ auszurechnen.

4. Schritt:

$\lambda$ setzt man jetzt in die Geradengleichung ein und erhält den Ortsvektor $\overrightarrow{OS}$ des Schnittpunktes (des Lotes).

5. Schritt:

Zum Schluss berechnet man den Abstand der Punkte $S$ und $P$ .

Beispiele

Berechne den Abstand des Punktes $P$ von der Geraden $g$ mit einer Hilfsebene.

\displaystyle d= \frac{|(\vec p - \vec a )\times \vec b|}{|\vec b|}

Lösungsweg 1 (Hilfsebene in Koordinatenform)

1. Schritt:

Man erstellt eine Hilfsebene $E$ , die durch den Punkt $P(1|-3|-3)$ geht und die zu dem Richtungsvektor $\vec{b}=\begin{pmatrix} -1 \\ 3 \\ 1 \end{pmatrix}$ orthogonal ist.

Es gilt $\vec{b}=\vec{n}$ . Deswegen ist die Normalform geeignet.

$E:\left[\overset\rightharpoonup x-\begin{pmatrix}1\\-3\\-3\end{pmatrix}\right]\circ\begin{pmatrix}-1\\3\\1\end{pmatrix}=0$

2. Schritt:

Die Ebene $E$ wandelt man in die Koordinatenform um.

$\left[\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}-\begin{pmatrix}1\\-3\\-3\end{pmatrix}\right]\circ\begin{pmatrix}-1\\3\\1\end{pmatrix}=0$

$\Rightarrow -(x_1-1)+3\cdot(x_2+3)+(x_3+3)=0$

$\Leftrightarrow -x_1+3x_2+x_3=-13$

3. Schritt:

In $x_1$ , $x_2$ und $x_3$ kann man jetzt den Vektor $\vec{X}$ der Geraden einsetzen, um $\lambda$ zu bestimmen.

$-(2-\lambda)+3(1+3\lambda)+(-3+\lambda)=-13$

$\Leftrightarrow11\lambda=-11$

$\Leftrightarrow\lambda=-1$

4. Schritt:

Man setzt nun $\lambda$ in die Geradengleichung $g$ ein, um den Schnittpunkt zu bestimmen.

$\overrightarrow{OS}=\begin{pmatrix} 2 \\ 1 \\ -3 \end{pmatrix}+(-1)\cdot \begin{pmatrix} -1 \\ 3 \\ 1 \end{pmatrix}=\begin{pmatrix} 3 \\ -2 \\ -4\end{pmatrix}$

5. Schritt:

Jetzt berechnet man den Abstand der beiden Punkte $P(1|-3|-3)$ und $S(3|-2|-4)$ .

$\displaystyle d$	$=$	$\displaystyle \sqrt{(3-1)^2+(-2-(-3))^2+(-4-(-3))^2}$
	↓	Vereinfache.
	$=$	$\displaystyle \sqrt{2^2+1^2+(-1)^2}$
	↓	Vereinfache.
	$=$	$\displaystyle \sqrt{6}$

Antwort: Der Abstand des Punktes $P(1|-3|-3)$ von der Geraden $g$ beträgt $d=\sqrt{6}\;\text{LE}$ .

Lösungsweg 2 (Hilfsebene in Normalform)

1. Schritt:

Man erstellt eine Hilfsebene $E$ , die durch den Punkt $P(1|-3|-3)$ geht und die zu dem Richtungsvektor $\vec{b}=\begin{pmatrix} -1 \\ 3 \\ 1 \end{pmatrix}$ orthogonal ist.

Es gilt $\vec{b}=\vec{n}$ . Deswegen ist die Normalform geeignet.

$E:\left[\overset\rightharpoonup x-\begin{pmatrix}1\\-3\\-3\end{pmatrix}\right]\circ\begin{pmatrix}-1\\3\\1\end{pmatrix}=0$

Man überspringt Schritt $2$ , weil schon die richtige Ebenenform gefunden ist.

3. Schritt:

Jetzt sucht man den Schnittpunkt der Ebene mit der Geraden. Hierfür setzt man $\vec{X}$ in die Ebene ein:

$E:\left[\begin{pmatrix}2\\1\\-3\end{pmatrix}+\begin{pmatrix}\lambda\cdot(-1)\\\lambda\cdot3\\\lambda\cdot1\end{pmatrix}-\begin{pmatrix}1\\-3\\-3\end{pmatrix}\right]\circ\begin{pmatrix}-1\\3\\1\end{pmatrix}=0$

Aufgelöst folgt:

$\Rightarrow -1\cdot(2-\lambda-1)+3\cdot(1+3\lambda+3)-3+\lambda+3 = 0$

$\Leftrightarrow \lambda+9\lambda+\lambda-1+12+0=0$

$\Leftrightarrow \lambda=-\dfrac{11}{11}=-1$

4. Schritt:

$\lambda=-1$ setzt man in die Geradengleichung $g$ ein, um den Schnittpunkt zu bestimmen.

$\overset\rightharpoonup{OS}=\begin{pmatrix} 2 \\ 1 \\ -3 \end{pmatrix}+(-1)\cdot \begin{pmatrix} -1 \\ 3 \\ 1 \end{pmatrix}=\begin{pmatrix} 3 \\ -2 \\ -4\end{pmatrix}$

5. Schritt:

Jetzt berechnet man den Abstand der beiden Punkte $P(1|-3|-3)$ und $S(3|-2|-4)$ .

$\displaystyle d$	$=$	$\displaystyle \sqrt{(3-1)^2+(-2-(-3))^2+(-4-(-3))^2}$
	↓	Vereinfache.
	$=$	$\displaystyle \sqrt{2^2+1^2+(-1)^2}$
	↓	Vereinfache.
	$=$	$\displaystyle \sqrt{6}$

Antwort: Der Abstand des Punktes $P(1|-3|-3)$ von der Geraden $g$ beträgt $d=\sqrt{6}\;\text{LE}$ .

Lösungsweg 3 (Minimierung des Abstandes)

1. Schritt:

Man überlegt sich die allgemeine Form der Koordinaten von Punkten auf der Geraden.

\displaystyle d= \frac{|(\vec p - \vec a )\times \vec b|}{|\vec b|}

2. Schritt:

Man berechnet den Abstand vom Punkt $P(1|-3|-3)$ mit den im Schritt $1$ ausgerechneten Punkten auf der Geraden. Hierfür benutzen wir die Formel zum Berechnen des Abstandes zweiter Punkte und setzen den Punkt $P$ und die Punkte auf der Geraden mit $\lambda$ ein.

\displaystyle d= \frac{|(\vec p - \vec a )\times \vec b|}{|\vec b|}

3. Schritt:

Wir haben einen klobigen Ausdruck für den Abstand erhalten. Dieser Ausdruck ist immer noch von $\lambda$ abhängig. Jedes $\lambda$ beschreibt einen Punkt auf der Geraden $g$ und jeder dieser Punkte hat einen eigenen Abstand.

Jetzt können wir vereinfachen, was unter der Wurzel steht.

\displaystyle d= \frac{|(\vec p - \vec a )\times \vec b|}{|\vec b|}

4. Schritt:

Der Abstand der Geraden vom Punkt $P$ ist gerade das Minimum dieser Funktion $d\left(\lambda\right)$ .

Da Abstände immer positiv sind, können wir auch das Minimum von $d^2$ bestimmen und dann die Wurzel ziehen.

\displaystyle d= \frac{|(\vec p - \vec a )\times \vec b|}{|\vec b|}

Wir erkennen die Form einer nach oben geöffneten Parabel und können die Formel für den Scheitelpunkt einer Parabel anwenden, um das Minimum von $d^2$ (also die y-Koordinate des Scheitelpunktes) zu berechnen:

\displaystyle d= \frac{|(\vec p - \vec a )\times \vec b|}{|\vec b|}

Die y-Koordinate ist:

$\displaystyle y$	$=$	$\displaystyle c-\dfrac{b^2}{4 \cdot a}$
	↓	Lies aus der Parabelgleichung die Werte für $a$ , $b$ und $c$ ab. Setze $a=11$ , $b=22$ und $c=17$ ein.
	$=$	$\displaystyle 17-\dfrac{22^2}{4\cdot11}$
	↓	Vereinfache den Bruch.
	$=$	$\displaystyle 17-11$
	↓	Vereinfache.
	$=$	$\displaystyle 6$

Demnach ist $d_{min}^2=6$ und $d_{min}=\sqrt{6}$

Alternativ kann auch über das Ableiten das Extremum der Funktion vom Abstandsquadrat bestimmt werden.

\displaystyle d= \frac{|(\vec p - \vec a )\times \vec b|}{|\vec b|}

Berechnung im Zweidimensionalen

Gegeben ist eine Gerade $\mathbf {g}\boldsymbol{:}\;\;\mathbf {x}\boldsymbol{=}\boldsymbol:\begin{pmatrix}\mathbf a\\\mathbf b\end{pmatrix}\boldsymbol+\mathbf\lambda\begin{pmatrix}\mathbf c\\\mathbf d\end{pmatrix}$ und ein Punkt $\mathbf P\;\boldsymbol=\begin{pmatrix}\mathbf e\\\mathbf f\end{pmatrix}$ . Dann lassen sich diese Objekte im Zweidimensionalen ins Dreidimensionale einbetten.

Man schreibt einfach für $g:\overset\rightharpoonup x=\begin{pmatrix}a\\b\\0\end{pmatrix}+\lambda\begin{pmatrix}c\\d\\0\end{pmatrix}$ und $P=\begin{pmatrix}e\\f\\0\end{pmatrix}$ und rechnet wie im Dreidimensionalen, der Abstand (im Zweidimensionalen) ist dann der ausgerechnete Wert.

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Abstand eines Punktes zu einer Geraden berechnen (Analytische Geometrie)

Berechnung im 3-dimensionalen Fall

Beispiel

Alternative schrittweise Berechnung mit einer Hilfsebene

Beispiele

Lösungsweg 1 (Hilfsebene in Koordinatenform)

1. Schritt:

2. Schritt:

3. Schritt:

4. Schritt:

5. Schritt:

Lösungsweg 2 (Hilfsebene in Normalform)

1. Schritt:

3. Schritt:

4. Schritt:

5. Schritt:

Lösungsweg 3 (Minimierung des Abstandes)

1. Schritt:

2. Schritt:

3. Schritt:

4. Schritt:

Wir erkennen die Form einer nach oben geöffneten Parabel und können die Formel für den Scheitelpunkt einer Parabel anwenden, um das Minimum von d2d^2d2 (also die y-Koordinate des Scheitelpunktes) zu berechnen:

Alternativ kann auch über das Ableiten das Extremum der Funktion vom Abstandsquadrat bestimmt werden.

Berechnung im Zweidimensionalen

Du hast noch nicht genug vom Thema?

Artikel

Wir erkennen die Form einer nach oben geöffneten Parabel und können die Formel für den Scheitelpunkt einer Parabel anwenden, um das Minimum von $d^2$ (also die y-Koordinate des Scheitelpunktes) zu berechnen: