Ein Vektor bezeichnet eine Verschiebung und wird durch jeden Pfeil repräsentiert, der
gleiche Länge
und gleiche Richtung
wie die betreffende Verschiebung hat.
Vektoren werden meistens mit einem Kleinbuchstaben mit einem Pfeil darüber benannt. Typische Vektorennamen sind also
Die einzelnen Pfeile bezeichnet man als Repräsentanten dieses Vektors. Sie sind alle parallel zueinander.
Hier sieht man einige Repräsentanten des Vektors .
Detaillierte Einführung
Eine schrittweise Einführung zum Thema findest du im Kurs Einführung in den Vektorbegriff (Vektoren in der Ebene I).
Video zur Einführung des Vektorbegriffs
Laden
Repräsentanten untersuchen
Im Applet kannst du die Punkte A und B sowie den Vektorpfeil selbst verschieben und erforschen, wann sich der zugehörige Vektor verändert.
Vektoren in Ebene und Raum
Der Vektor liegt in der x-y-Ebene
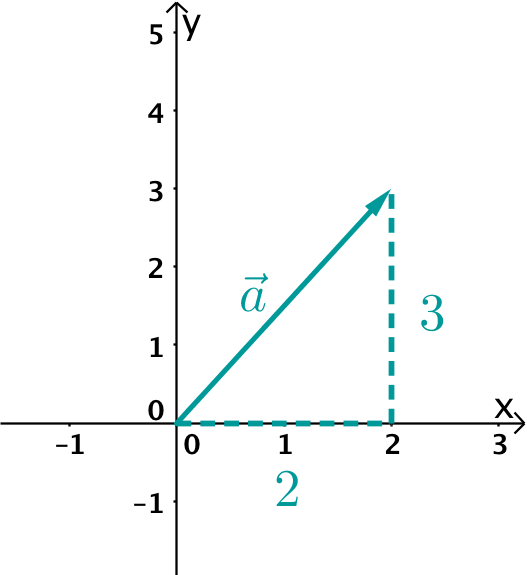
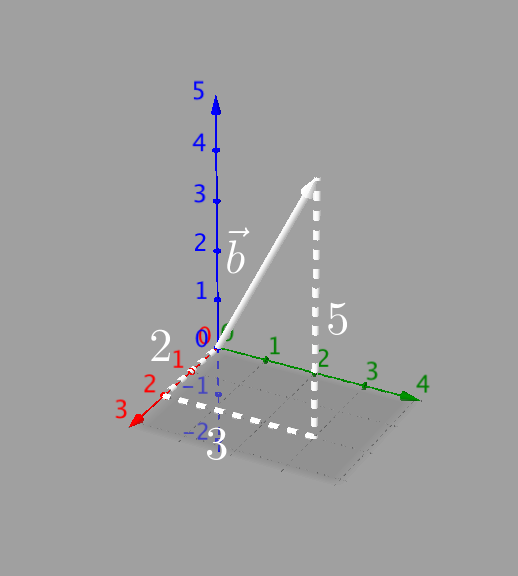
Der Vektor liegt im Raum
Die Koordinaten eines Vektors werden mit verschiedenen Schreibweisen bezeichnet. Beispiele sind:
Länge eines Vektors
Die Länge oder der Betrag eines Vektors wird mit (oder auch ) bezeichnet und berechnet sich wie folgt:
, falls in der Ebene liegt
, falls im dreidimensionalen Raum liegt.
Im Artikel Länge eines Vektors findet man mehr Informationen dazu.
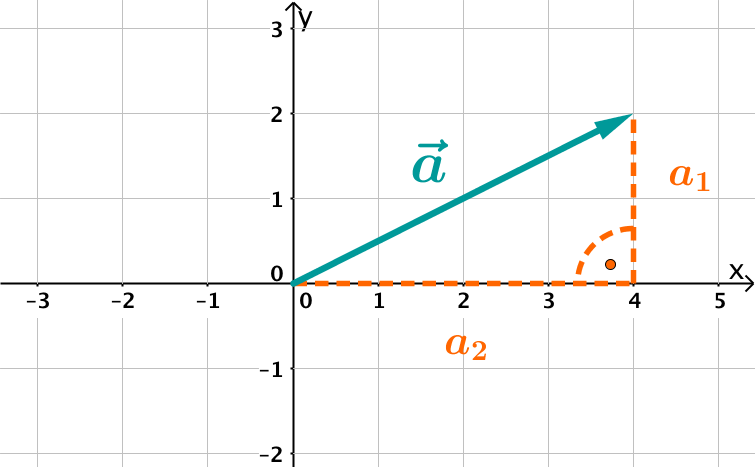
Beziehungen zwischen zwei Vektoren
Parallelität
Zwei Vektoren und sind zueinander parallel, wenn der eine ein Vielfaches des anderen ist:
Orthogonalität
Zwei Vektoren und sind zueinander orthogonal (= senkrecht), wenn ihr Skalarprodukt gleich 0 ist.
Ein Vektor , der orthogonal
zu einem anderen Vektor oder
zu einer Geraden oder
zu einer Ebene
steht, nennt man Normalvektor (oder auch Normalenvektor) von , oder .
Vor allem Ebenen, aber auch Geraden, werden mit Normalvektoren in einer Normalform sehr einfach dargestellt.
Rechnungen mit Vektoren
Mit Vektoren lässt sich ähnlich wie bei Zahlen rechnen. Man kann also:
Vektoren addieren und subtrahieren,
Vektoren mit einer Zahl skalar multiplizieren (= strecken oder stauchen),
zwei Vektoren miteinander multiplizieren.
Wichtig: Es gibt mehr als eine Art, Vektoren miteinander zu multiplizieren. Beim Skalarprodukt ist das Ergebnis eine Zahl (= ein Skalar), während beim Kreuzprodukt ein weiterer Vektor entsteht.
Eine weitere wichtige Rechnung, die man mit Vektoren machen kann, ist die sogenannte Matrix-Vektor-Multiplikation.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Berechnung eines Vektors zwischen zwei Punkten
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
