Aufgaben zum Strahlensatz oder Vierstreckensatz
Hier findest du Aufgaben zum Strahlensatz bzw. Vierstreckensatz. Lerne, fehlende Größen mithilfe des Strahlensatzes zu berechnen!
- 1
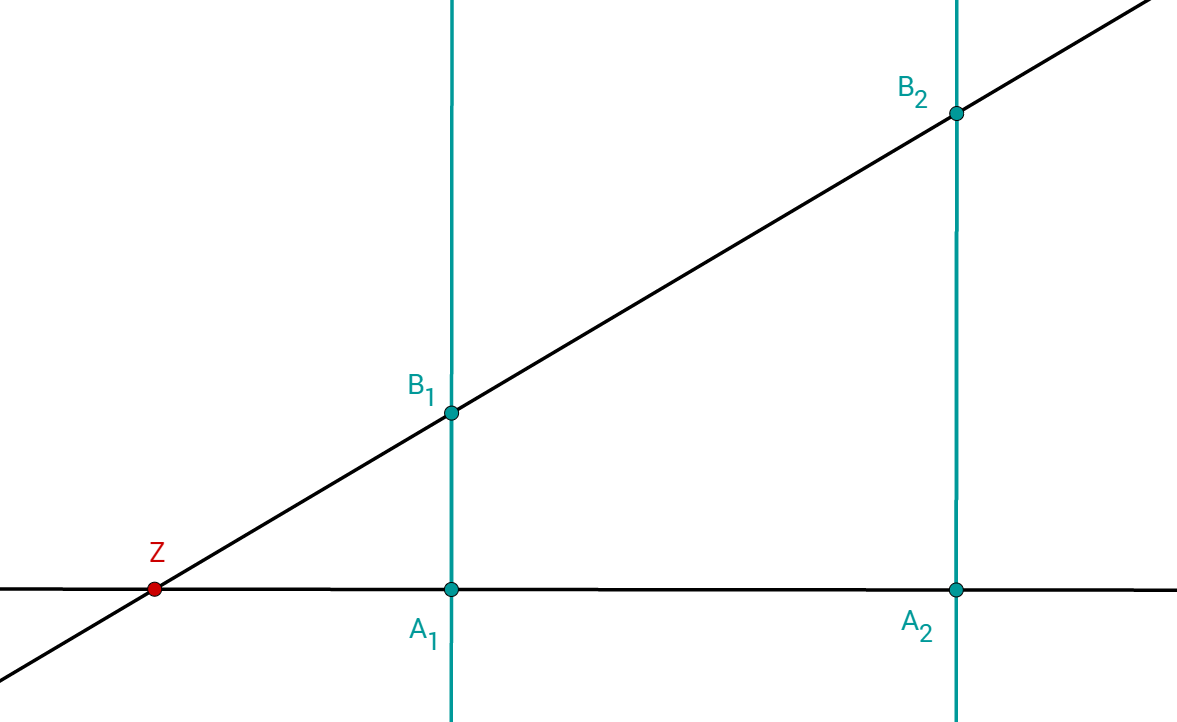
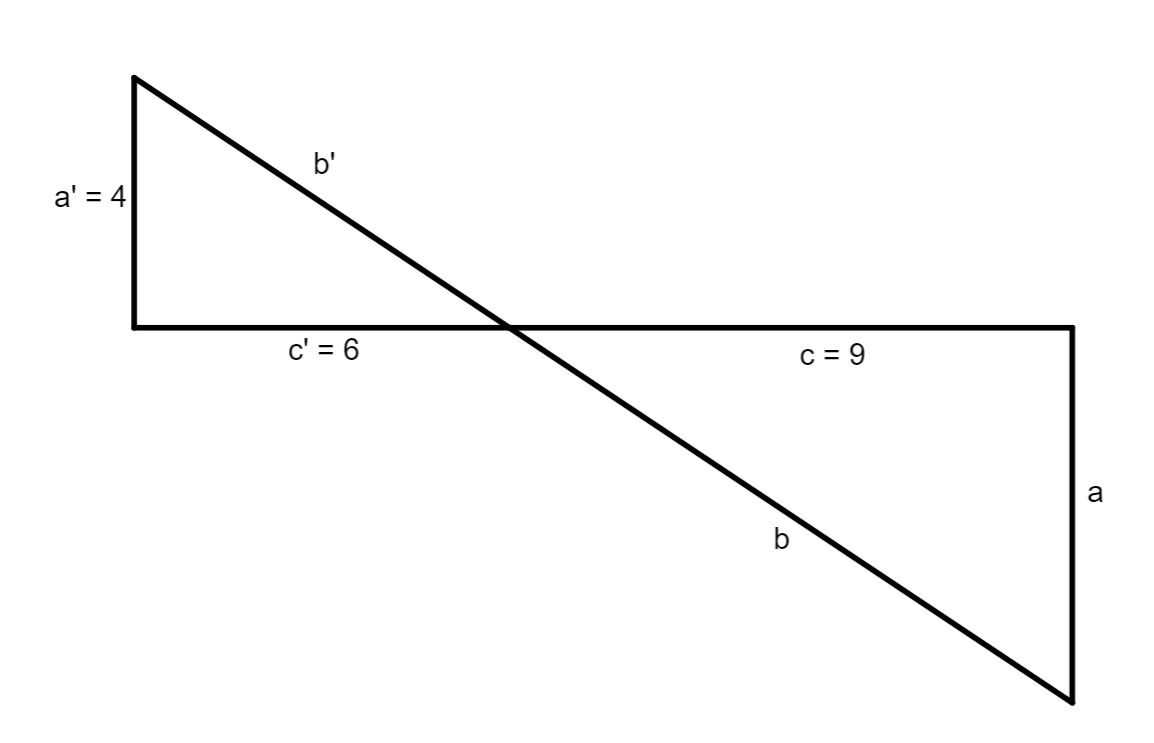
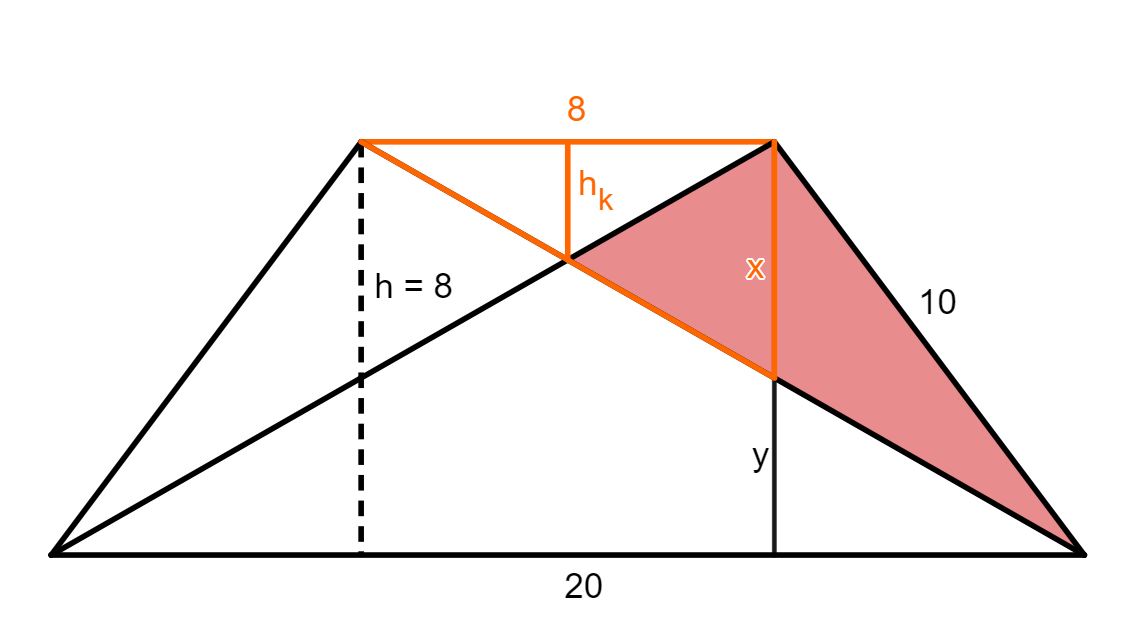
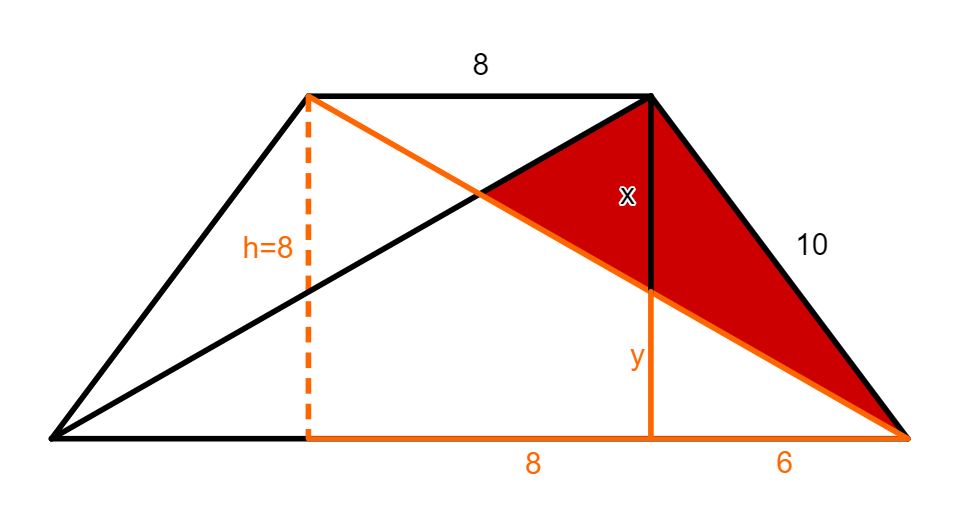
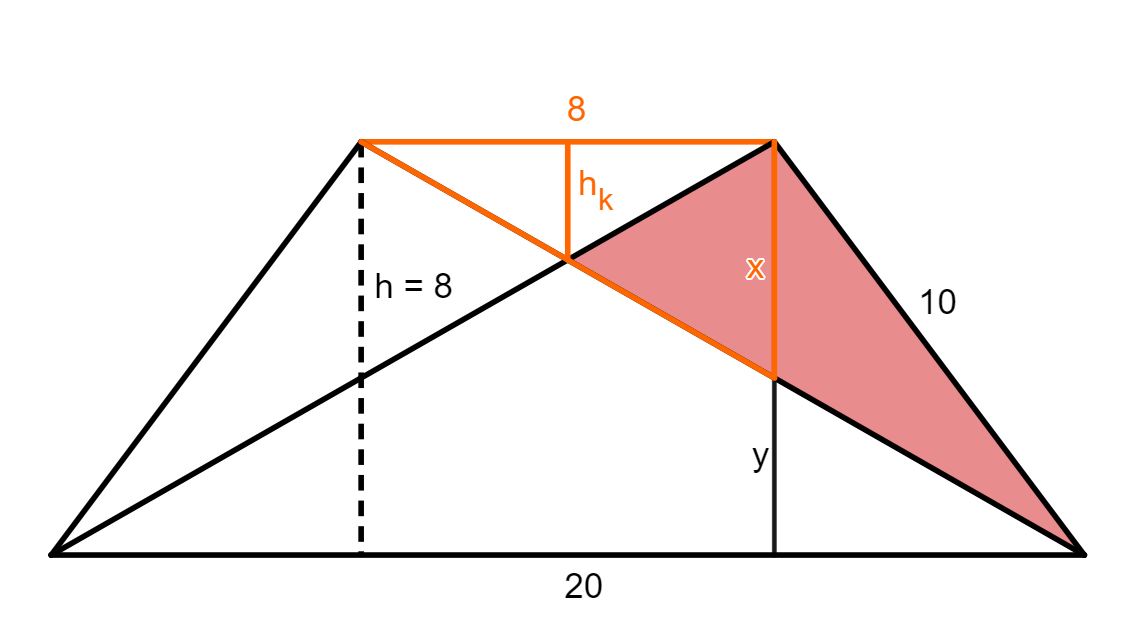
Betrachte die Figur rechts, in der die Geraden durch und zueinander parallel sind. Es gilt: , und .
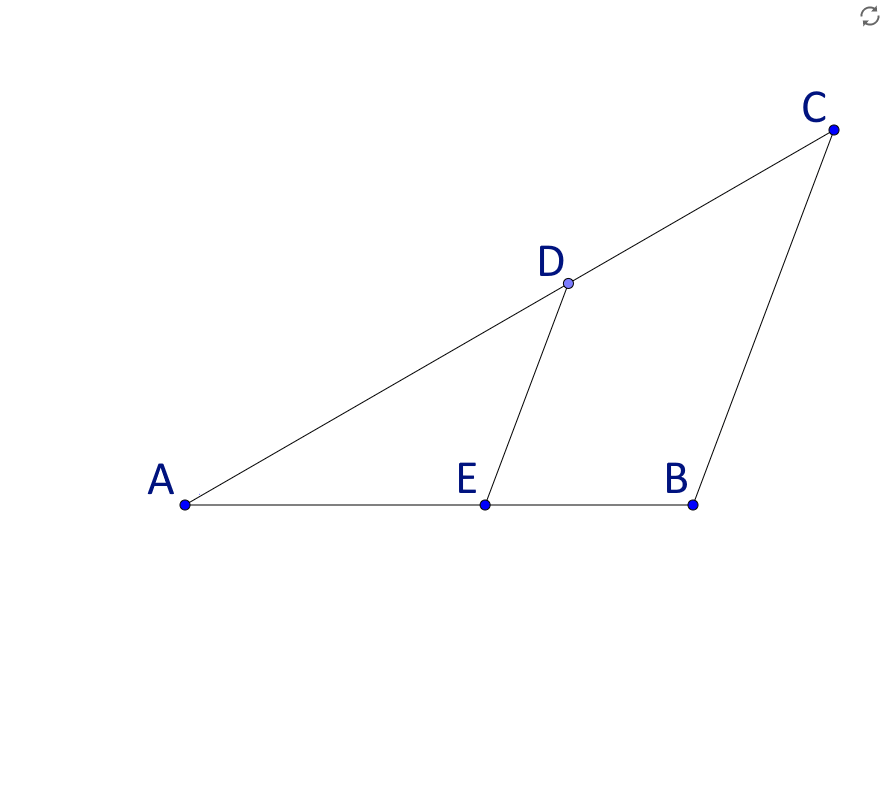
Wie lang ist die Strecke in ?
Wenn gilt , wie lange ist dann in ?
- 2
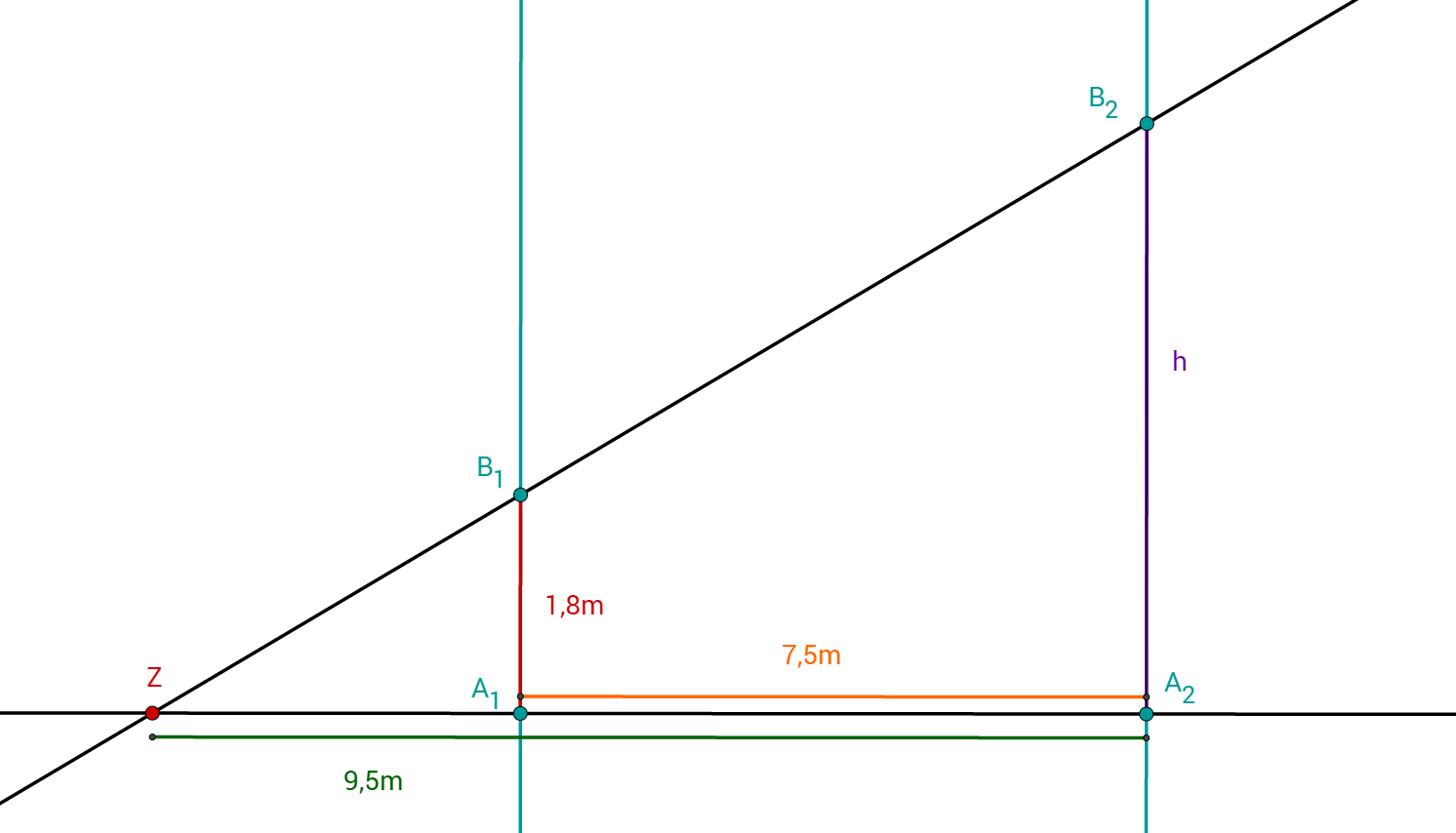
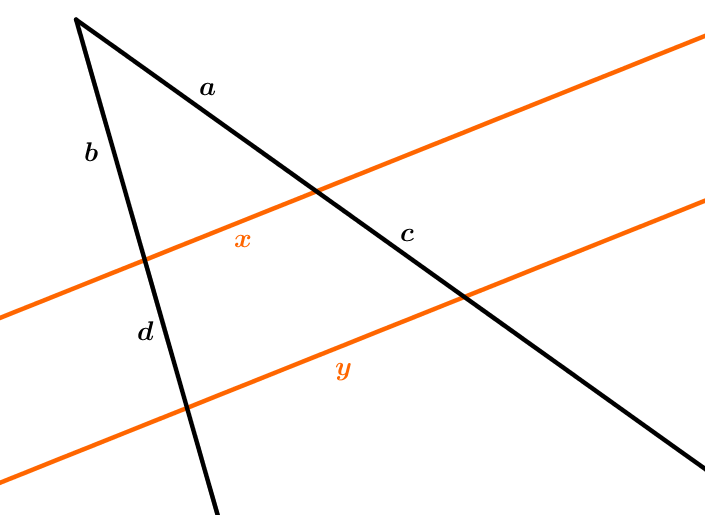
Betrachte die Figur rechts.
Die Geraden und sind zueinander parallel. Außerdem gilt , und .
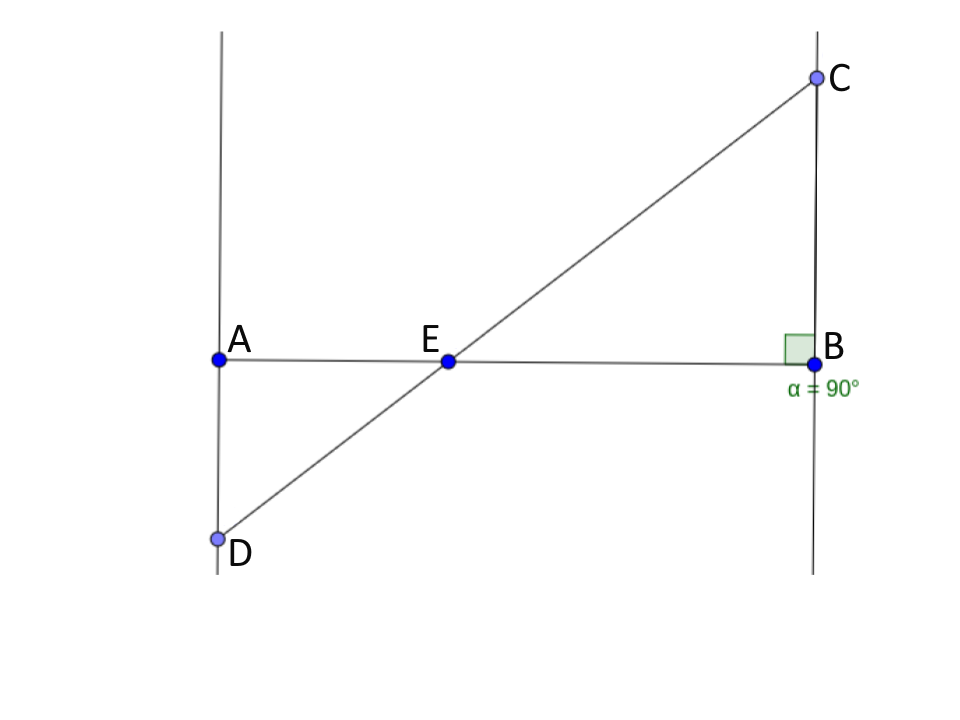
Berechne die Länge der Strecke in .
Begründe, warum du die Länge der Strecke nicht mit Hilfe des Strahlensatzes berechnen kannst.
- 3
Entscheide, ob du den Strahlensatz anwenden darfst und die gesuchte Strecke berechnen kannst!
Gegeben:
Gesucht:
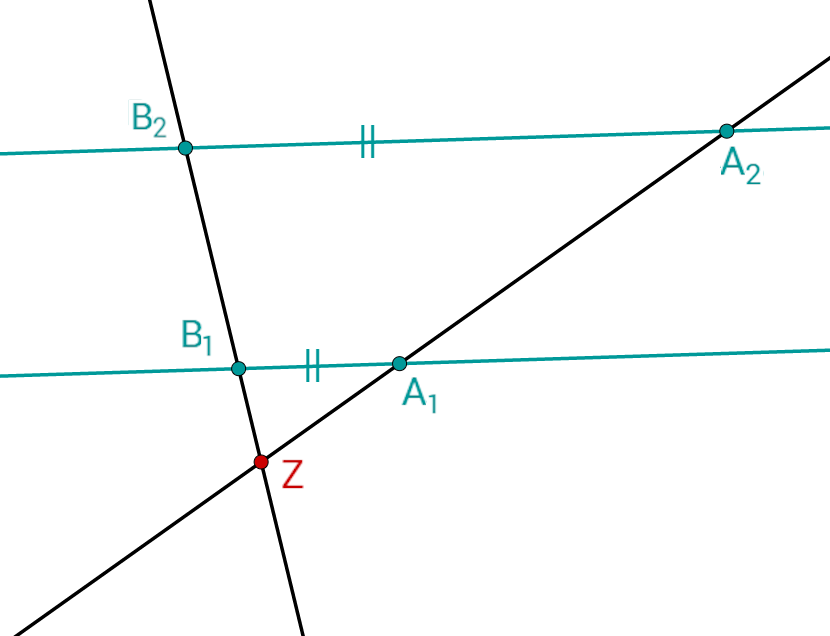
Gegeben:
Gesucht:
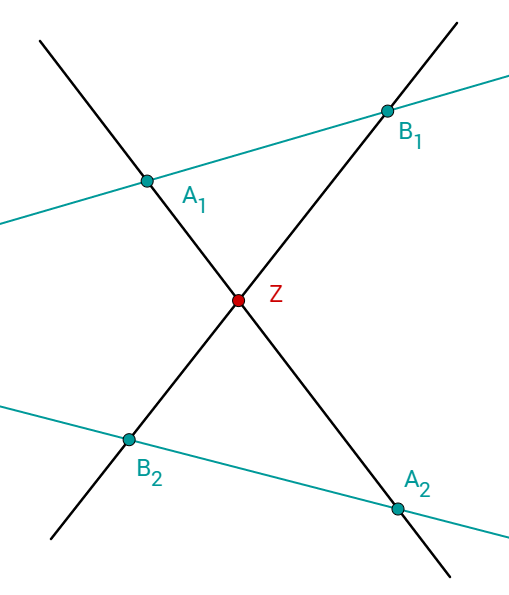
Gegeben:
Gesucht:
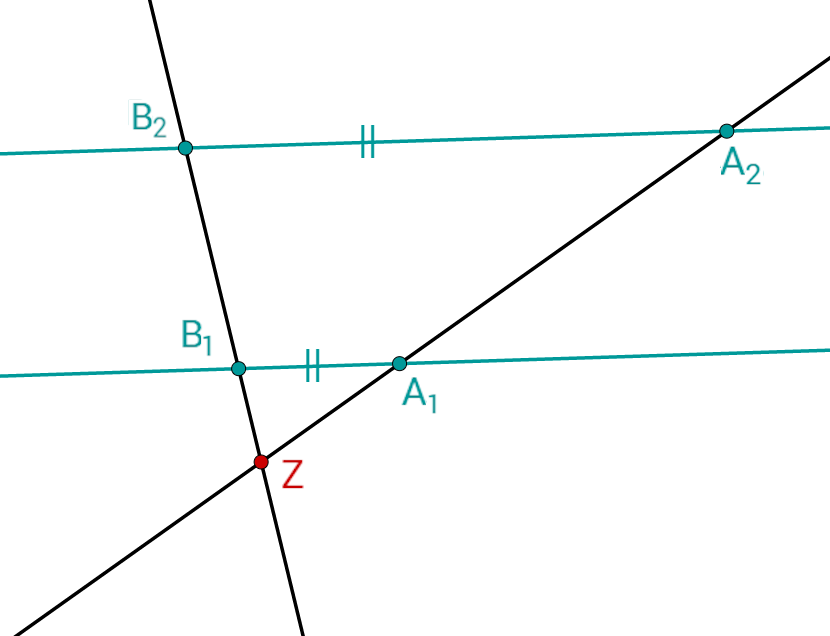
Gegeben:
Gesucht:
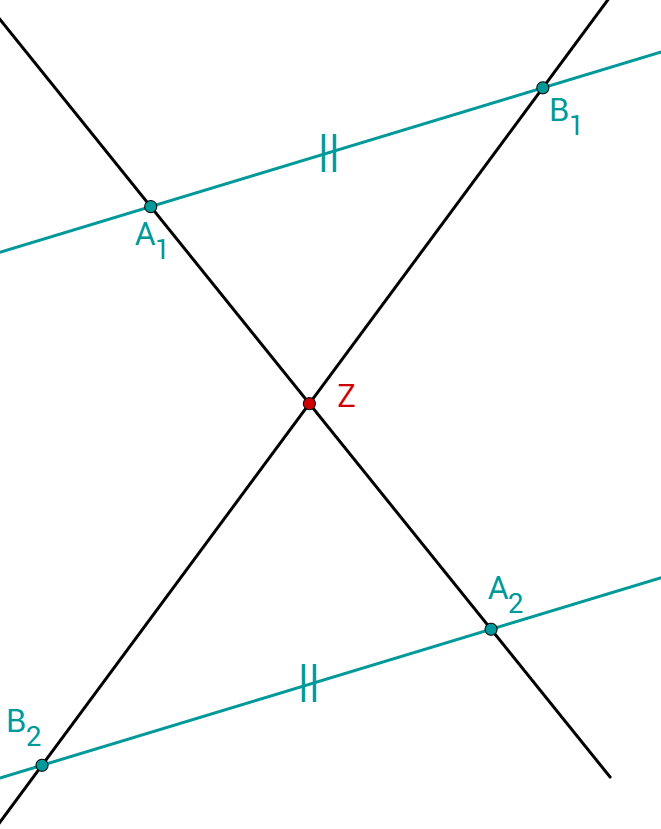
- 4
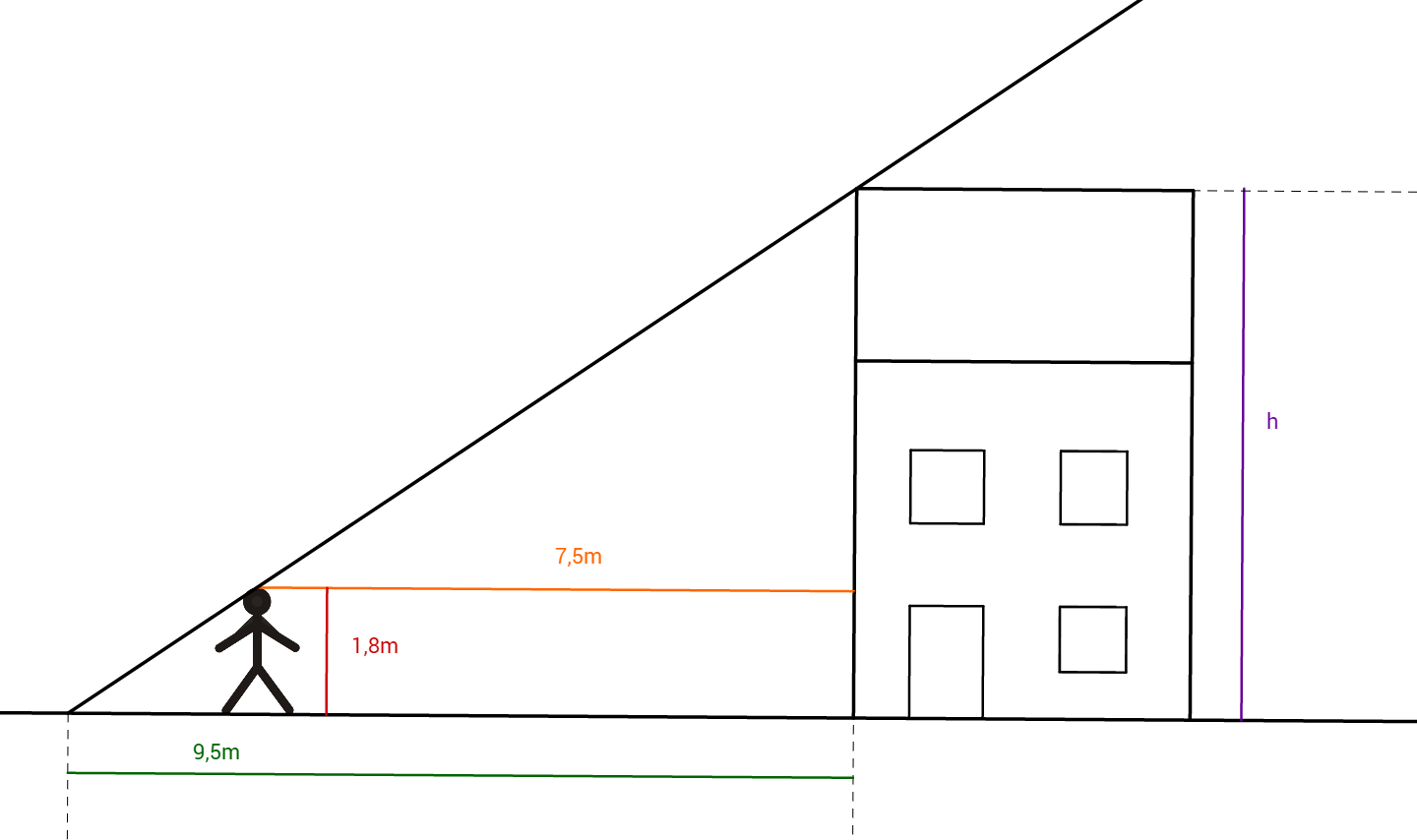
Klaus will ein Haus mithilfe des Hausschattens ausmessen. Dazu misst Klaus zuerst den Abstand vom Haus bis zum Endpunkt des Schattens. Dieser Abstand beträgt genau .
Anschließend stellt sich Klaus, der groß ist, genau an den Punkt, ab dem er im Schatten ist. Diesen Ort markiert er und misst wieder den Abstand von dieser Markierung zum Haus. Dieser beträgt .
Benutze den Strahlensatz, um die Höhe des Hauses zu berechnen!
 m
m - 5
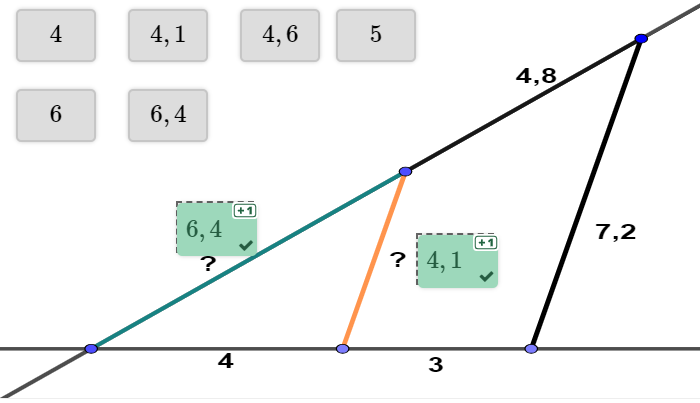
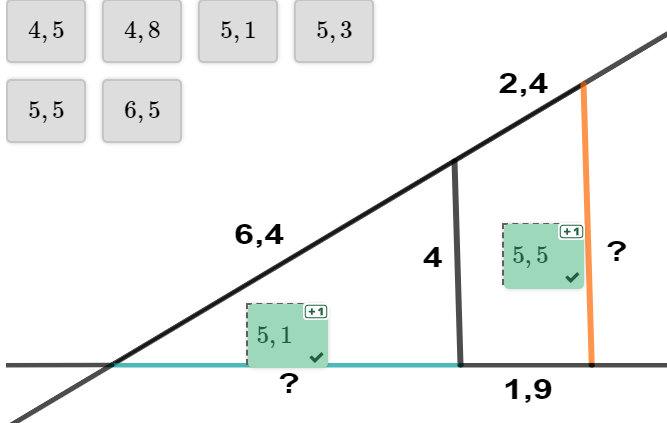
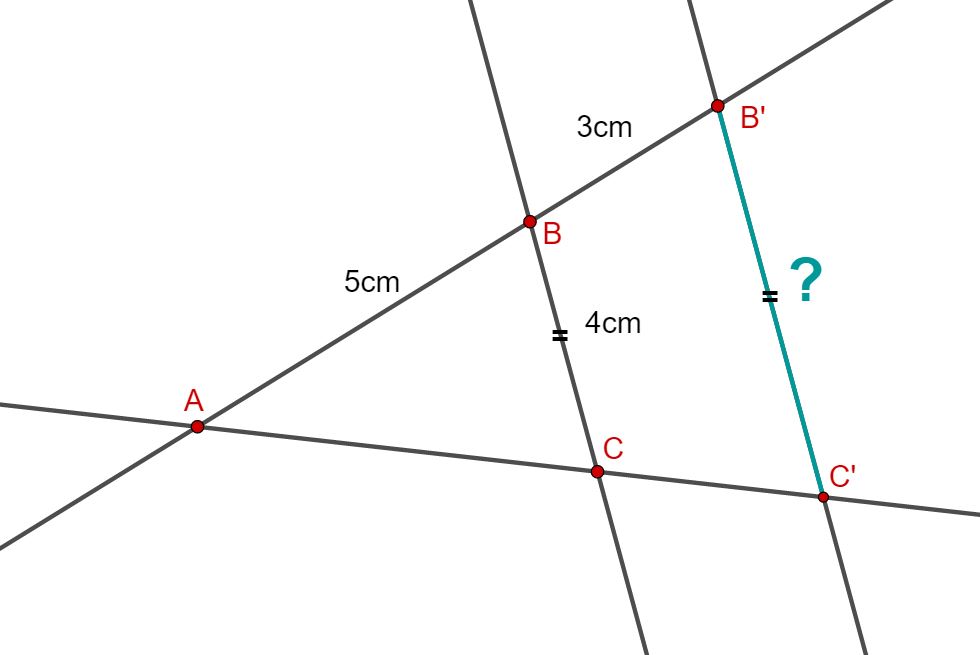
Die Strecken , und sind gegeben. Berechne die Länge der türkis markierten Strecke !
- 6
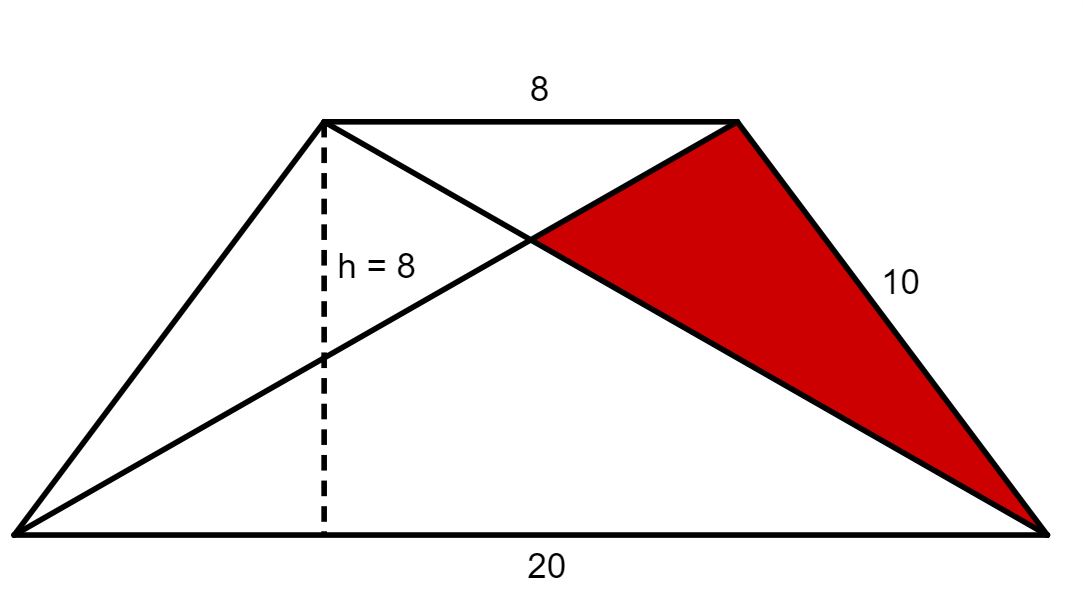
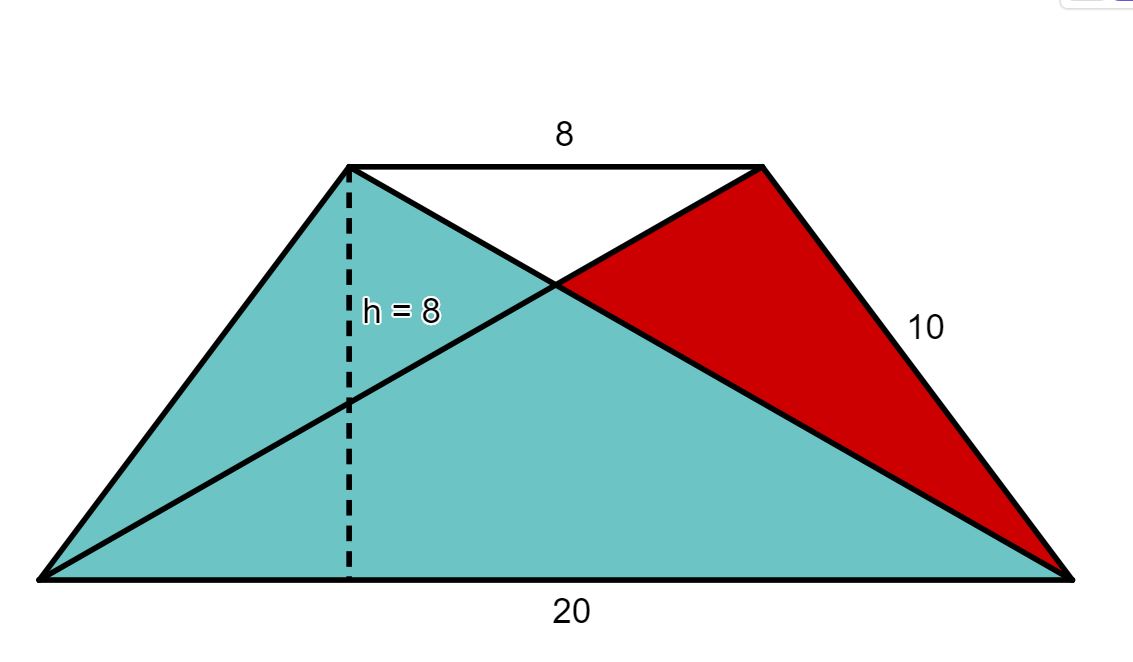
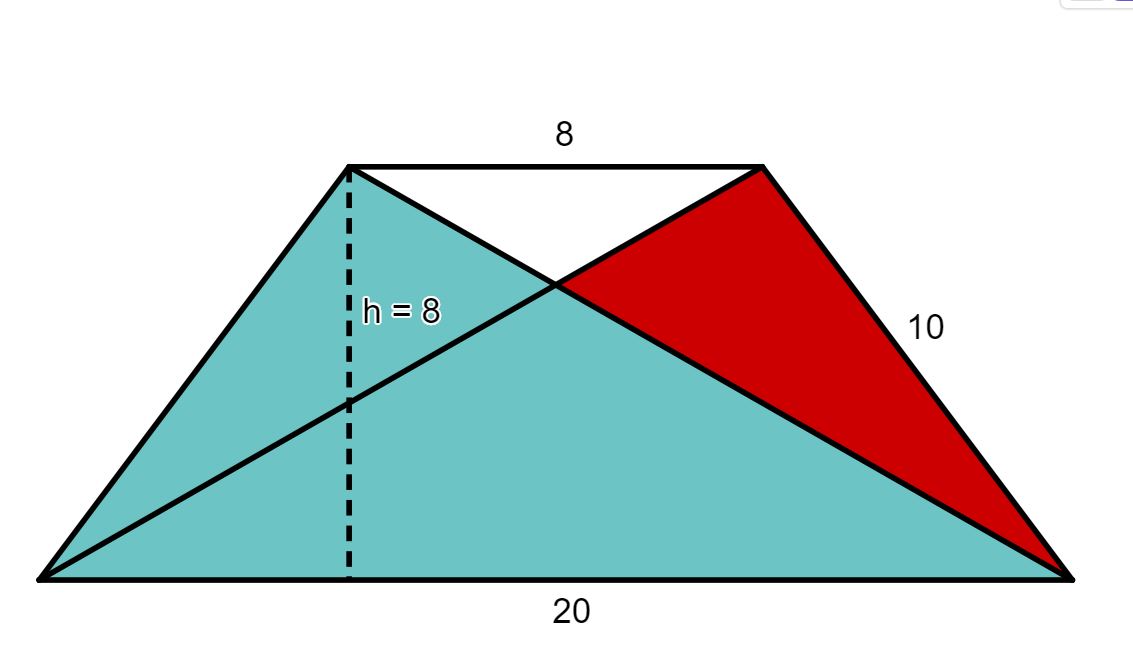
Gegeben sei die nebenstehende Figur mit den Seiten und .
Berechne die Länge der Strecke mit Hilfe des Strahlensatzes.
Berechne die Länge der Strecke mit Hilfe des Strahlensatzes.
- 7
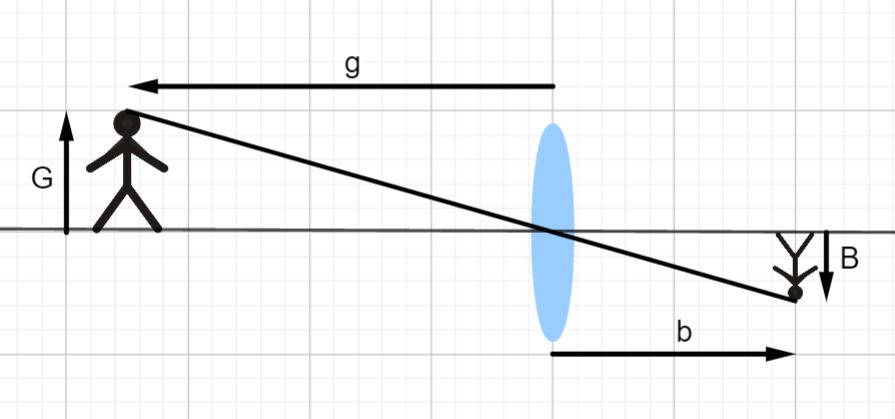
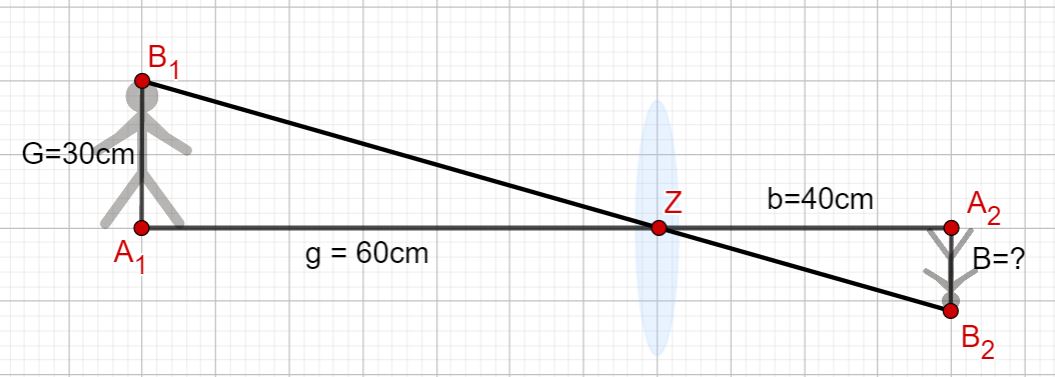
Eine Figur wird durch eine Linse auf einen Bildschirm abgebildet. Dabei dreht sich das Bild um und wird verkleinert. Der Abstand der Figur zur Linse wird in der Physik auch Gegenstandsweite genannt. Der Abstand des Bildes zur Linse wird auch Bildweite genannt.
Die Größe der Figur ist (Gegenstandsgröße) und die Größe des Bildes ist .
Du hast nun die Gegenstandsweite, Bildweite und die Größe des Gegenstandes gegeben und sollst die Größe des Bildes auf der Leinwand berechnen.
cm - 8
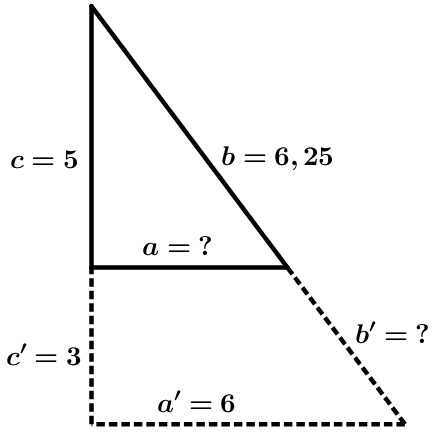
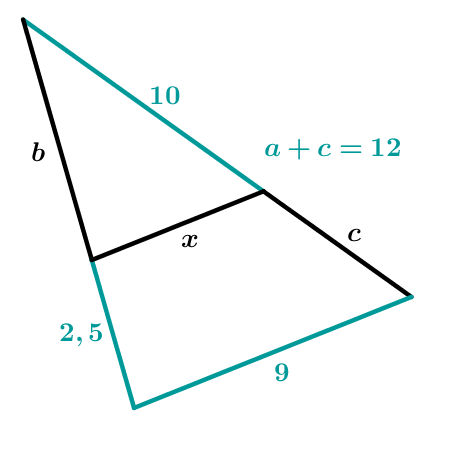
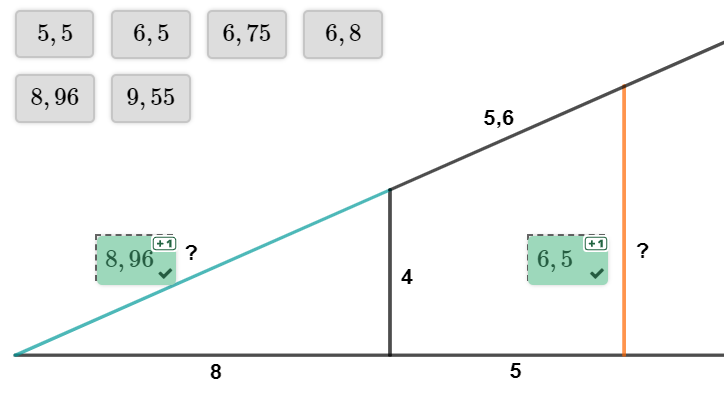
Gegeben sei folgende Figur, mit den Längen , , und und .
Berechne die Länge der Strecke in mit Hilfe des Strahlensatzes.
Berechne die Länge der Strecke in mit Hilfe des Strahlensatzes.
- 9
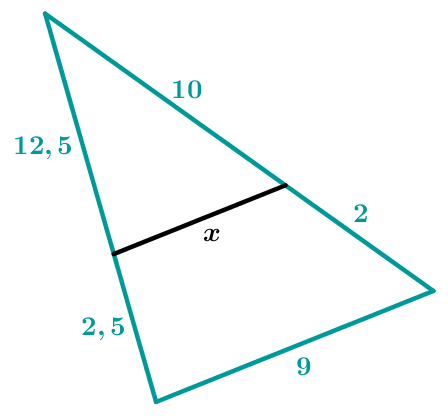
Gegeben sei die folgende Figur mit den Seiten .
Berechne mithilfe der gegebenen Werte den Wert für !
- 10
- 11
Berechne mit den Strahlensätzen die unbekannten Längen.
- 12
Berechne mit den Strahlensätzen die unbekannten Längen.
- 13
Berechne mit den Strahlensätzen die unbekannten Längen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?