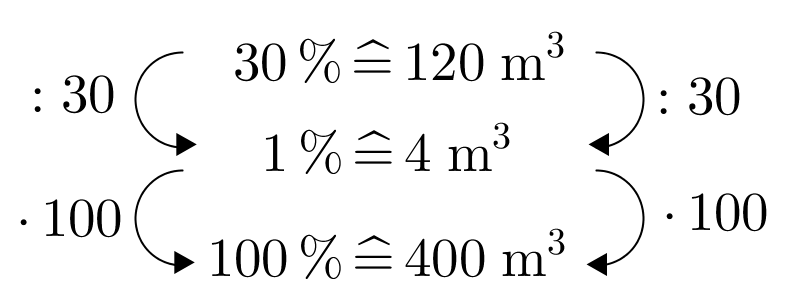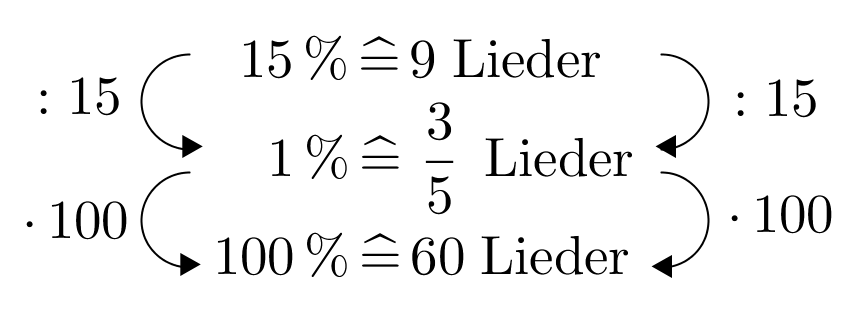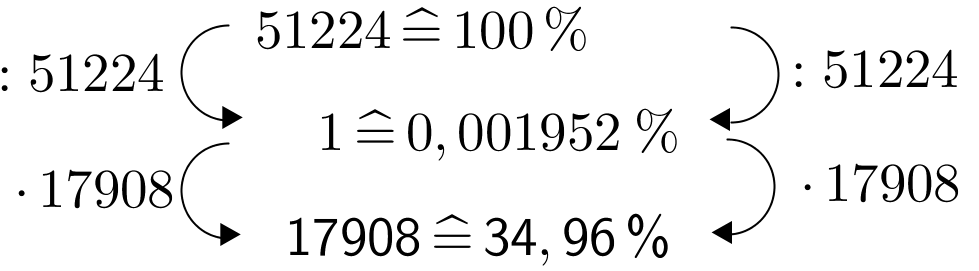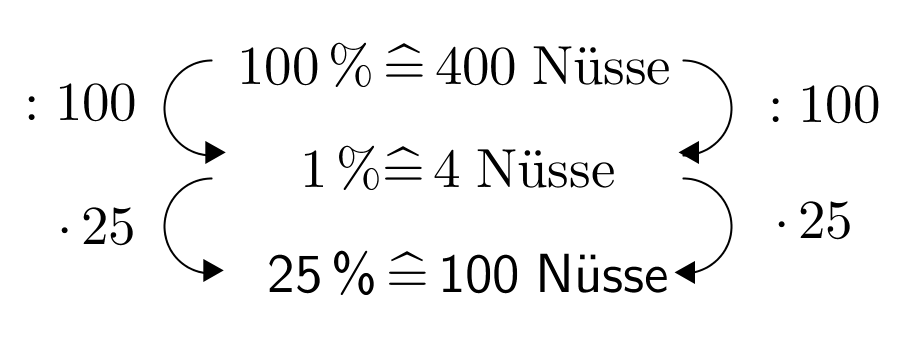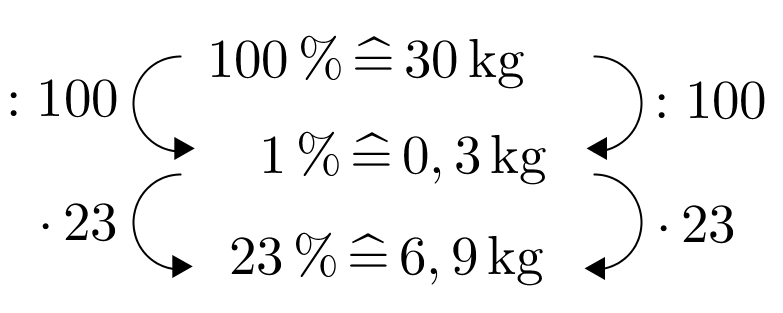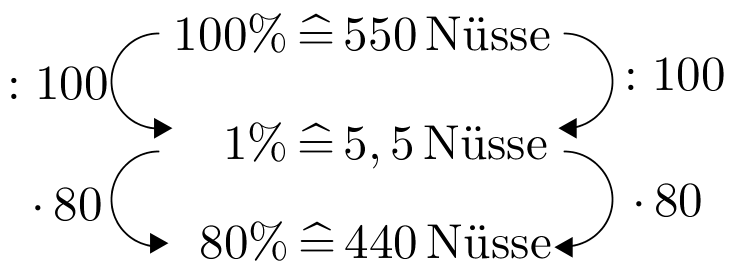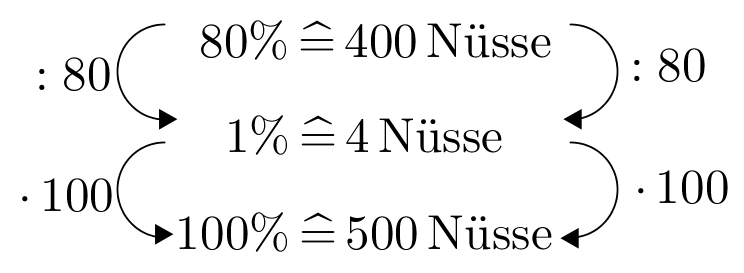Aufgaben zu Grundwert, Prozentwert und Prozentsatz
Hier findest du Aufgaben zur Prozentrechnung. Lerne, Grundwert, Prozentwert und Prozentsatz zu bestimmen!
- 1
Markiere Grundwert, Prozentsatz und Prozentwert.

Bei den 500 Nüssen, die das Eichhörnchen vergraben hat, sind Haselnüsse dabei. Das sind der Nüsse.
Von den 200 Haselnüssen findet das Eichhörnchen 180 Stück wieder. Das sind 90% .
Im Jahr darauf hat das Eichhörnchen 400 Nüsse als Wintervorrat vergraben, findet aber 500 Nüsse wieder. Die 100 Nüsse gehören anscheinend nicht ihm, werden aber gut dazu beitragen über den Winter zu kommen. Es hat 125% Nüsse gefunden.
- 2
Bestimme den Grundwert mittels Dreisatz.
sind des Wassers in einem See. Berechne wie viel Wasser insgesamt im See ist.
m³Auf der Samstagabend-Party der Tanzschule Serlo wird auch Walzer getanzt. der gespielten Lieder eignen sich dafür. Es werden an einem Abend 9 Walzertitel gespielt. Berechne wie viele Lieder insgesamt gespielt werden.
Lieder
- 3
In Berlin und München wurden Leute befragt, ob sie eine Katze besitzen. Das Ergebnis ist in dieser Tabelle dargestellt:
Katzenbesitzer
Anzahl der Befragten
Berlin
17908
51224
München
479
1276
Ist der Anteil der Katzenbesitzer in Berlin größer als in München?

- 4
Letztes Jahr hat ein Baby-Eichhörnchen 400 Nüsse vergraben und 25% davon nicht wiedergefunden. Wie viele Nüsse blieben unentdeckt?
Nüsse - 5
In einer Klasse sind 17 Jungen und 8 Mädchen. Wie viel Prozent Jungen bzw. Mädchen sind in der Klasse?
- 6
In Deutschland ist es üblich in einem Restaurant 10% Trinkgeld zu geben. Der Vater von Hans bekommt eine Rechnung über 30,70€. Wie viel Trinkgeld bekommt die Kellnerin?

Trinkgeld Autor: Alan Light Quelle: Wikimedia Commons
€ - 7
Ein Architekt berechnet einem Bauherren als Honorar 8,5% der Baukosten. Wie hoch ist sein Honorar bei einem Einfamilienhaus mit Baukosten in Höhe von 290300 €?
€ - 8
Eine Sachbearbeiterin zahlt monatlich 22% Lohnsteuer, das sind 435,60 €. Wie hoch ist ihr Bruttolohn?
€ - 9
Ein Auto setze 40% der in der Tankfüllung steckenden Energie in Bewegung um, nämlich 600 MJ (Energie-Einheit "Megajoule"). Der Rest geht z.B. durch Wärme über die Abgase verloren. Wie viele MJ sind das?
MJ - 10
Lieblingsfilm
Die Klasse 8a wird nach ihrem Lieblingsfilm befragt.
40% von den 25 abgegebenen Stimmzetteln enthalten den Film "Friss oder Stirb".
Eva ist sich bei 9 Klassenkamerad*innen sicher, dass sie diesen Film gewählt haben.
Wie viele Schüler*innen haben für den Film gestimmt, von denen Eva das nicht weiß?

- 11
Justus findet im Keller ein altes Videospiel, in dem man tierähnliche Wesen fangen kann. 20% dieser "Taschenmonster" besitzt er bereits und er weiß, dass das 30 sind. Wie viele davon gibt es insgesamt in dem Spiel?
Taschenmonster - 12
Jana möchte wissen, wie schnell sie "Friss oder Stirb - das Buch zum Film" lesen kann. Sie liest die erste Seite auf ihrem E-Reader und stellt fest, dass sie für die erste Seite 110 Sekunden braucht. Ihr E-Reader zeigt ihr an, dass sie nach der ersten Seite 0,8% des Buches gelesen hat. Schätze ab, wie lang sie brauchen wird, um das Buch zu lesen.
h - 13
Julia lässt sich ein Bad ein. Weil die Badewanne nach 5 min erst zu 15% befüllt ist, wird ihr langweilig und sie geht kurz telefonieren. Als sie zurückkommt, steht das Bad unter Wasser. Wie lange hat sie mindestens telefoniert?
- 14
An einer Wahl nahmen 426.688 Wahlberechtigte teil und stimmten je für eine der drei Parteien A, B und C. Die Partei B erhielt 70% der Stimmen von A, die Partei C hingegen 80% der Stimmen von B. Wie viele Stimmen erhielt jede Partei?
- 15
Die Masse des herumliegenden Beton-Steins beträgt nach Schätzung des Maurers 10 kg, nach Schätzung des Architekten 16 kg.
- 16
Die Schule spendet dem Naturschutzbund 20% der Einnahmen vom Faschingsball. Wie viel Geld muss die Schule mindestens einnehmen, um 150 € spenden zu können?
€ - 17
Fabian wiegt 60 kg. Nachdem er eine Woche lang einen Magen-Darm-Virus hatte, wiegt er nur noch 58,8 kg. Wie viel Prozent seines ursprünglichen Körpergewichts hat er verloren?
% - 18
Um ein Zimmer mit Holz zu verkleiden, sind Holzpaneele vorhanden. Die Fläche, die verkleidet werden soll, ist groß.
Wie viele Paneele müssen noch nachgeliefert werden, wenn mit Verschnitt zu rechnen ist?
(Runde auf zwei Nachkommastellen.)
- 19
Die Klasse 7b soll für das nächste Jahr entweder den sprachlichen oder den naturwissenschaftlichen Zweig wählen. 12 Schüler*Innen entscheiden sich für Sprachen und 18 für die Naturwissenschaften. Wie viel Prozent der Klasse sind das jeweils?
- 20
Melanie hat eine Trefferquote von 80% beim Elfmeterschießen. Im Training soll sie 20 Elfmeter schießen. Mit wie vielen Toren kann sie rechnen?

Elfmeterschießen Autor: Emkaer Quelle: Wikipedia
Tore - 21
Herr X. gewinnt im Lotto. Er spendet 8% seines Lottogewinns für den Bau eines Spielplatzes in der Nachbarschaft. Er überweist dafür 6464€.
Bestimme, wie viel Geld ihm vom Lottogewinn noch übrig bleibt.
€ - 22
Von einem 30 kg schweren Polstersessel sind 23% aus Stoff, 50% aus Holz und der Rest aus Leder. Wieviel kg an Stoff, Holz und Leder braucht man für 40 Sessel?
- 23
Der Schuldirektor unterschreibt Zeugnisse. Er hat bereits 270 Zeugnisse fertig.
Die stellvertretende Direktorin fragt ihn, wie lange er noch braucht. Daraufhin antwortet er: "Ich habe bereits 45%."
Wie viele Zeugnisse muss der Direktor insgesamt unterschreiben?
Zeugnisse - 24
Beim Braten von Fleisch gehen ca. 25% des Gewichtes beim Erhitzen verloren. Wie viel Fleisch muss eingekauft werden, wenn nach dem Braten 180 g vorliegen soll?
g - 25
Eine Sonnenblume ist groß. Bis sie ausgewachsen ist, wächst sie noch um .

Um wie viel Zentimeter wächst sie noch?
cmWie groß ist sie, wenn sie ausgewachsen ist?
cm
- 26
Im Tank eines Autos befinden sich 30 Liter Benzin. Auf einem Ausflug an den See werden des Benzins verbraucht.

Wie viel Liter Benzin wurden verbraucht?
lWie viel Liter Benzin sind jetzt noch im Tank?
l
- 27
Ein Eichhörnchen braucht im Winter 400 Nüsse. Es hat im Herbst 550 Nüsse vergraben. Im Winter findet es von den im Herbst vergrabenen Nüssen wieder.
Kommt es über den Winter?
Wie viele Nüsse muss das Eichhörnchen dafür mindestens vergraben?
Nüsse
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?