🎓 Ui, fast schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung.
Springe zum Inhalt oder Footer
SerloDie freie Lernplattform
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.

Für eine ganzrationale Funktion ff dritten Grades mit der Definitionsmenge Df=RD_{f}=\mathbb{R} gelten folgende Gleichungen: I. f(0)=0\quad f(0)=0 II. f′(0)=0f^{\prime}(0)=0 III. f(−3)=−3f(-3)=-3 IV. f′(−3)=−1f^{\prime}(-3)=-1

Der zugehörige Graph in einem kartesischen Koordinatensystem wird mit GfG_{f} bezeichnet.

  1. Beschreiben Sie in Worten, welche Eigenschaften der Graph von f aufgrund obiger Gleichungen hat. (2 BE)

  2. Bestimmen Sie die Funktionsgleichung von f\mathrm{f}.

    [Mögliches Ergebnis: f(x)=−13x3−43x2f(x)=-\frac{1}{3} x^{3}-\frac{4}{3} x^{2} ] (5 BE)

  3. Im Folgenden wird die Funktion gg mit g(x)=f(x)g(x)=f(x) und der im Vergleich zu DfD_{f} eingeschränkten Definitionsmenge Dg=[−4,5;1]D_{g}=[-4{,}5 ; 1] betrachtet. Ihr Graph in einem kartesischen Koordinatensystem wird mit Gg\mathrm{G}_{\mathrm{g}} bezeichnet.

    Ermitteln Sie die Wertemenge Wg\mathrm{W}_{\mathrm{g}} der Funktion g. Bestimmen Sie dazu die Koordinaten sämtlicher Extrempunkte. (8 BE)

  4. Bestimmen Sie die Koordinaten des Wendepunktes des Graphen der Funktion g. (3 BE)

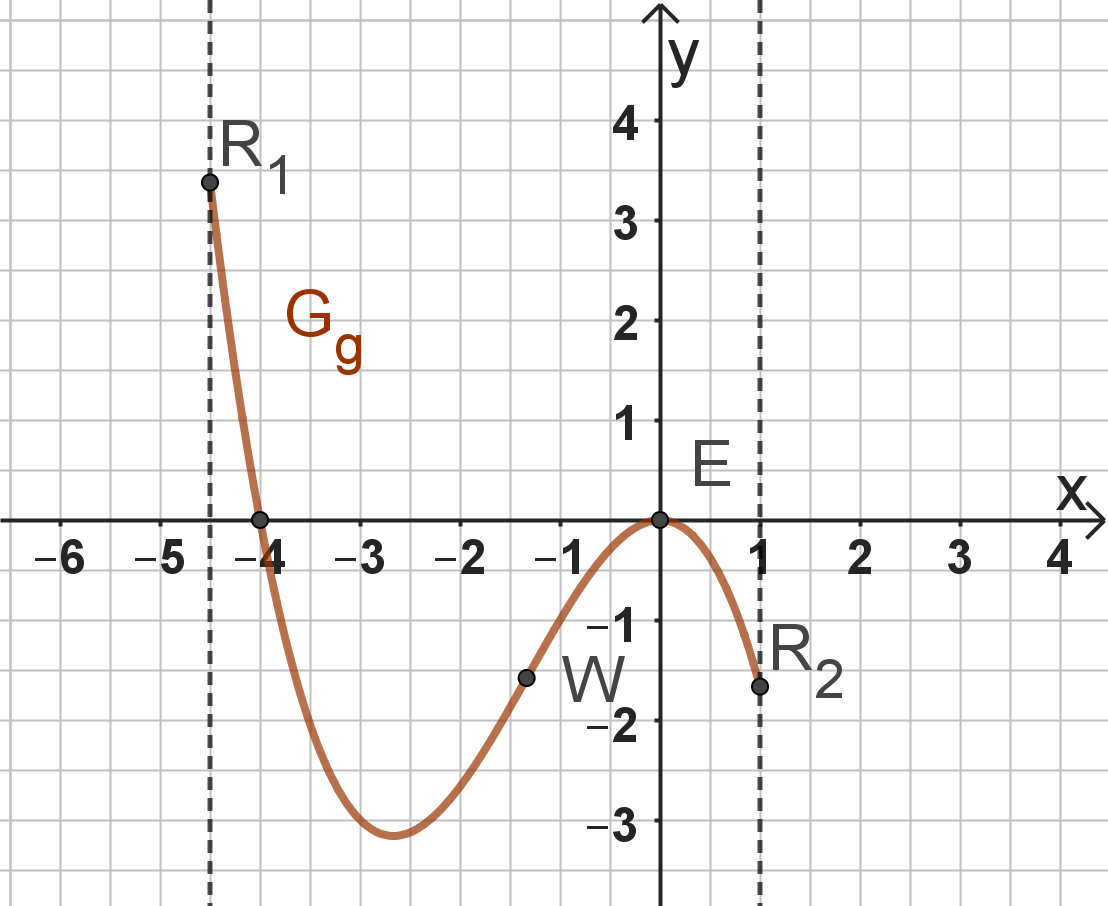
  5. Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse den Graphen Gg\mathrm{G}_{\mathrm{g}} in ein geeignetes kartesisches Koordinatensystem. Ermitteln Sie dazu die Nullstellen der Funktion g. Maßstab für beide Achsen: 1LE=1 cm1 \mathrm{LE}=1 \mathrm{~cm} (5 BE)

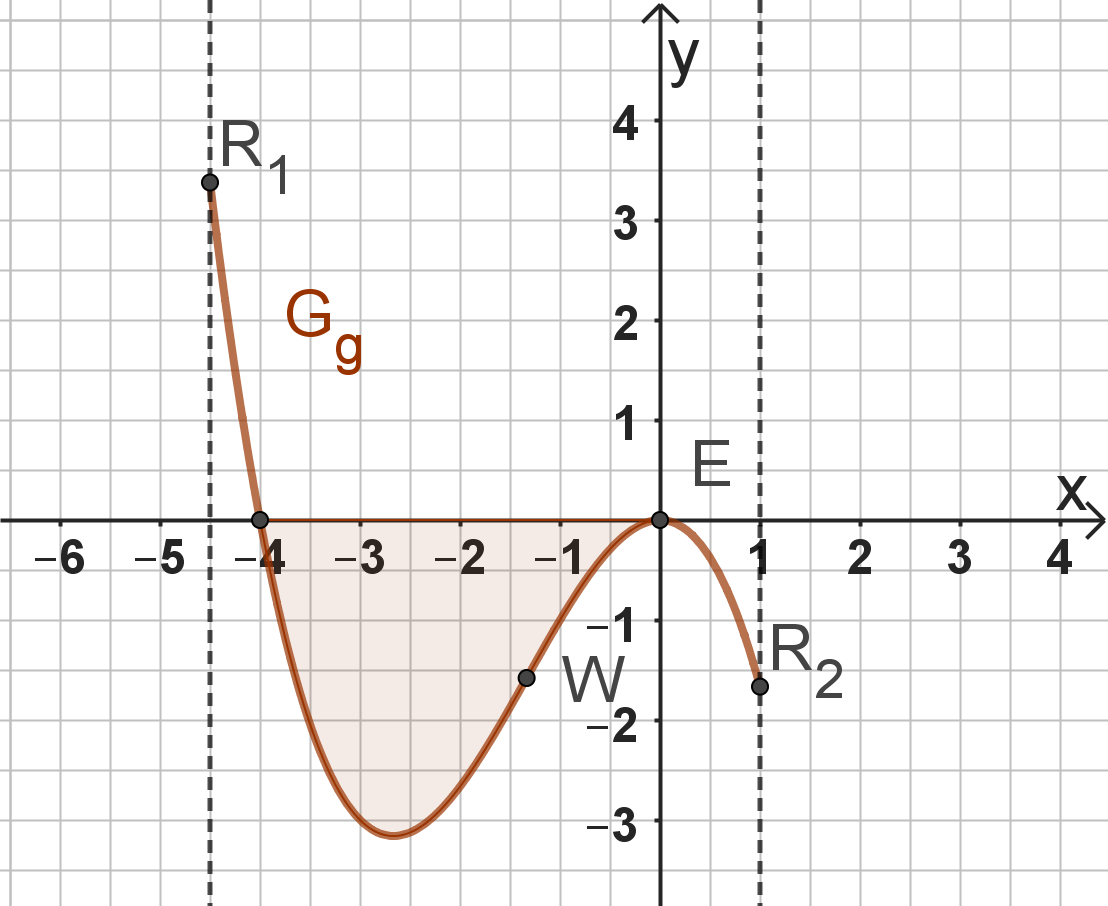
  6. Der Graph der Funktion gg und die x-Achse schließen im III. Quadranten des Koordinatensystems ein endliches Flächenstück ein. Berechnen Sie die Maßzahl des Flächeninhalts dieses Flächenstücks. (3 BE)