Teil 2, Analysis I

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Für eine ganzrationale Funktion $f$ dritten Grades mit der Definitionsmenge $D_{f} = ℝ$ gelten folgende Gleichungen: I. $f (0) = 0$ II. $f^{'} (0) = 0$ III. $f (- 3) = - 3$ IV. $f^{'} (- 3) = - 1$
Der zugehörige Graph in einem kartesischen Koordinatensystem wird mit $G_{f}$ bezeichnet.
1. Beschreiben Sie in Worten, welche Eigenschaften der Graph von f aufgrund obiger Gleichungen hat. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steckbriefaufgaben
  $I) f (0) = 0$
  Der Graph verläuft also durch $P (0 | 0)$ , den Ursprung des Koordinatensystems.
  $I I) f^{'} (0) = 0$
  Die Steigung im Ursprung ist 0.
  Insgesamt: Im Ursprung ist also eine Stelle mit waagerechter Tangente (Extrempunkt oder Terrassenpunkt)
  $I I I) f (- 3) = - 3$
  Der Graph verläuft durch den Punkt $Q (- 3 | - 3)$ .
  $I V) f^{'} (- 3) = - 1$
  Der Graph hat also im Punkt $Q (- 3 | - 3)$ die Steigung $m = - 1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setzt man in f ein, bekommt man Funktionswerte.
  Setzt man in die erste Ableitung $f^{'}$ ein, so bekommt man Steigungen.
2. Bestimmen Sie die Funktionsgleichung von $f$ .
  [Mögliches Ergebnis: $f (x) = - \frac{1}{3} x^{3} - \frac{4}{3} x^{2}$ ] (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Steckbriefaufgaben
  allgemeiner Funktionsterm
  Da es sich um eine ganzrationale Funktion vom Grad 3 ist und du nichts über die Symmetrie des zugehörigen Graphen weißt, ist der allgemeine Funtkionsterm:
  $f (x) = a x^{3} + b x^{2} + c x + d$
  Die Ableitungsfunktion ist somit:
  $f^{'} (x) = 3 a x^{2} + 2 b x + c$
  Bedingungsgleichungen
  Setze die Werte aus der Aufgabenstellung ein:
  $I) a \cdot 0^{3} + b \cdot 0^{2} + c \cdot 0 + d = 0 \Rightarrow d = 0$
  $I I) 3 a \cdot 0^{2} + 2 b \cdot 0 + c = 0 \Rightarrow c = 0$
  Verwende $c = 0$ und $d = 0$ direkt in den nächsten Bedingungsgleichungen:
  $I I I) a \cdot (- 3)^{3} + b \dot{(} - 3)^{2} = - 3$
  $I I I) - 27 a + 9 b = - 3$
  und
  $I V) 3 a \cdot (- 3)^{2} + 2 b \cdot (- 3) = - 1$
  $I V) 27 a - 6 b = - 1$
  Gleichungssystem lösen
  Löse das System zum Beispiel mit dem Additionsverfahren:
  $\begin{array}{lccll} - 27 a & + 9 b & = - 3 \\ + & 27 a & - 6 b & = - 1 \\ 3 b & = - 4 & | : 3 \\ b & = - \frac{4}{3} \end{array}$
  Setze $b = - \frac{4}{3}$ in eine der beiden Gleichungen ein, um $a$ zu berechnen.
  $27 a - 6 \cdot (- \frac{4}{3})$ $=$ $- 1$
  $27 a + 8$ $=$ $- 1$ $- 8$
  $27 a$ $=$ $- 9$ $: 27$
  $a$ $=$ $- \frac{1}{3}$
  Insgesamt ist der Term also, wie im Teilergebnis vorgegeben: $f (x) = - \frac{1}{3} x^{3} - \frac{4}{3} x^{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Stelle einen allgemeinen Funktionsterm für $f$ auf und bilde die erste Ableitung $f^{'}$ .
  Setze die Werte der Bedingungsgleichungen $I) - I V)$ in die allgemeine Funktionsgleichung ein.
  Löse das entstandene Gleichungssystem.
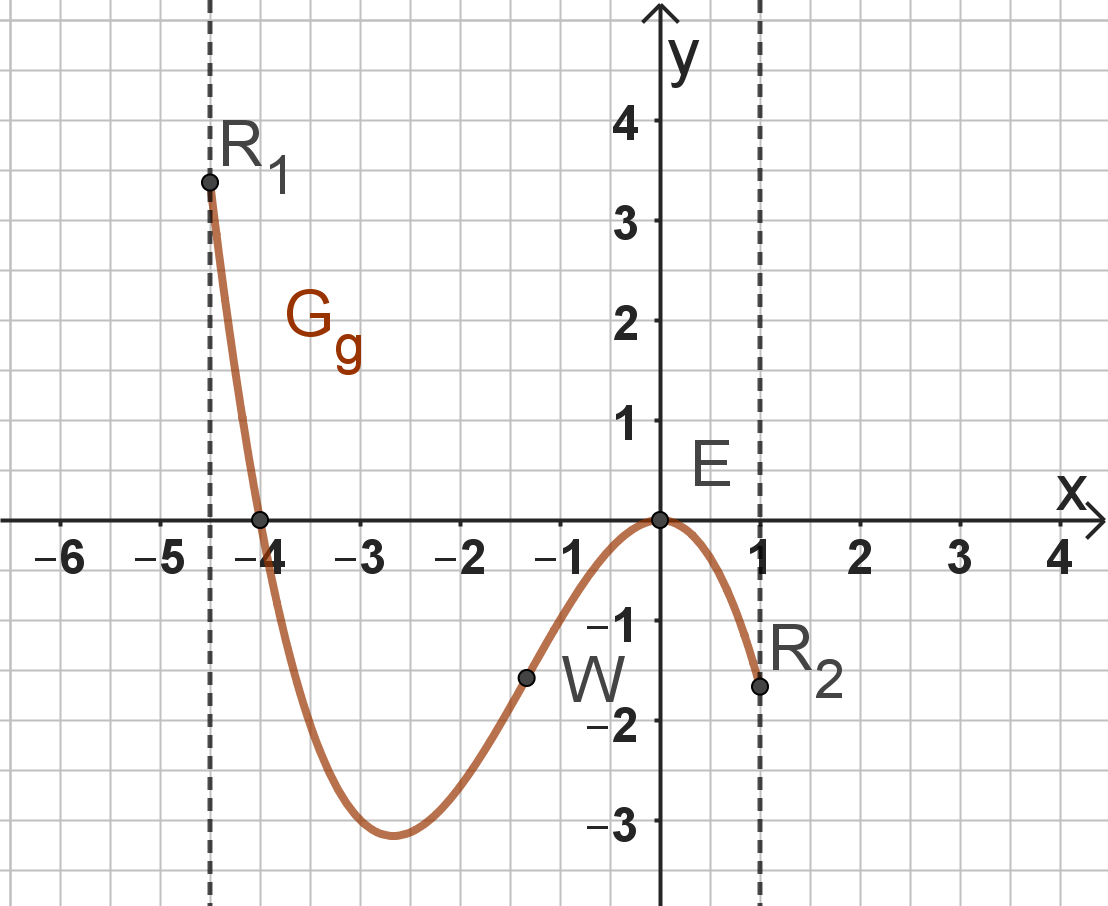
3. Im Folgenden wird die Funktion $g$ mit $g (x) = f (x)$ und der im Vergleich zu $D_{f}$ eingeschränkten Definitionsmenge $D_{g} = [- 4,5; 1]$ betrachtet. Ihr Graph in einem kartesischen Koordinatensystem wird mit $G_{g}$ bezeichnet.
  Ermitteln Sie die Wertemenge $W_{g}$ der Funktion $g$ . Bestimmen Sie dazu die Koordinaten sämtlicher Extrempunkte. (8 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertemenge
  Randextrempunkte
  Da beide Ränder der Definitionsmenge eingeschlossen sind, gibt es zwei Randextrempunkte:
  $R_{1} (- 4,5 | g (- 4,5))$ und $R_{2} (1 | g (1))$
  Bestimme die Funktionswerte durch einsetzen:
  $g (- 4,5) = \frac{27}{8} = 3,375$
  $g (1) = - \frac{5}{3} \approx - 1,67$
  Weitere Extrempunkte
  Bestimme mithilfe der Nullstellen der 1. Ableitung die übrigen Extrempunkte:
  $g^{'} (x) = - x^{2} - \frac{8}{3} x$
  und somit
  $g^{'} (x)$ $=$ $0$
  $- x^{2} - \frac{8}{3} x$ $=$ $0$
  ↓
  Klammere $- x$ aus.
  $- x (x + \frac{8}{3})$ $=$ $0$
  Nach dem Satz vom Nullprodukt gibt es die beiden Nullstellen $x = 0$ und $x = - \frac{8}{3} \approx - 2,67$ .
  Bei $x = 0$ ist eine Extremstelle von $g$ , da es eine einfache Nullstelle von $g^{'}$ ist und dort somit ein Vorzeichenwechsel stattfindet.
  Es ist $g^{''} (x) = - 2 x - \frac{8}{3}$ und $g^{''} (0) = - \frac{8}{3} < 0 \Rightarrow H P$
  Der Hochpunkt liegt bei $H P (0 | 0)$ , da aus der Aufgabenstellung bekannt ist, dass der Graph durch den Ursprung verläuft.
  Für $x = - \frac{8}{3}$ ist $g^{''} (- \frac{8}{3}) = - 2 \cdot (- \frac{8}{3}) - \frac{8}{3} = \frac{8}{3} > 0 \Rightarrow T P$
  $g (- \frac{8}{3}) = - \frac{1}{3} \cdot {(- \frac{8}{3})}^{3} - \frac{4}{3} \cdot {(- \frac{8}{3})}^{2} = - \frac{256}{81}$
  Der Tiefpunkt hat die Koordinaten $T P (- \frac{8}{3} | - \frac{256}{81})$ .
  Wertemenge
  Die beiden Extrempunkte $R_{1} (- 4,5 | \frac{27}{8})$ und $T P (- \frac{8}{3} | - \frac{256}{81})$ bestimmen die Wertemenge. Verwende dazu den kleinsten und größten y-Wert:
  $W = [- \frac{256}{81}; \frac{27}{8}]$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Art der Extremstellen ist nicht verlangt!
  Bestimme die Koordinaten der Randextrempunkte an beiden Rändern von $D_{g}$ durch Einsetzen in $g$ .
  Bestimme die übrigen Extremstellen im Definitionsbereich:
  Bilde die 1. Ableitung $g^{'}$ .
  Bestimme die Nullstellen von $g^{'}$ und entscheide mithilfe der Vielfachheit, ob es sich um Extremstellen handelt.
  Bestimme die zugehörigen Funktionswerte.
  Betrachte alle berechneten y-Koordinaten, um die Wertemenge anzugeben.
4. Bestimmen Sie die Koordinaten des Wendepunktes des Graphen der Funktion $g$ .
  (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
  Leite die Ableitungsfunktion $g^{'} (x) = - x^{2} - \frac{8}{3} x$ erneut ab:
  $g^{''} (x) = - 2 x - \frac{8}{3}$
  Bestimme die Nullstelle von $g^{''}$ :
  $g^{''} (x)$ $=$ $0$
  $- 2 x - \frac{8}{3}$ $=$ $0$ $+ \frac{8}{3}$
  $- 2 x$ $=$ $\frac{8}{3}$ $: (- 2)$
  $x$ $=$ $- \frac{4}{3}$
  Der Wert $x = - \frac{4}{3} \approx - 1,33$ liegt in der Definitionsmenge.
  Da es sich um eine einfache Nullstelle handelt, hat $G_{g^{''}}$ dort einen Vorzeichenwechsel und es ist tatsächlich eine Wendestelle von $G_{g}$ .
  Durch Einsetzen in $g$ erhältst du den zugehörigen Funktionswert:
  $g (- \frac{4}{3}) = - \frac{128}{81} \approx - 1,58$
  Der Wendepunkt liegt also bei $W (- \frac{4}{3} | - \frac{128}{81})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Nullstelle der 2. Ableitung und zeige, dass der Graph $G_{g^{''}}$ dort einen Vorzeichenwechsel hat.
  Bestimme den zugehörigen Funktionswert.
5. Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse den Graphen $G_{g}$ in ein geeignetes kartesisches Koordinatensystem. Ermitteln Sie dazu die Nullstellen der Funktion $g$ . Maßstab für beide Achsen: $1 LE = 1 c m$ (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
  Nullstellen bestimmen
  $g (x)$ $=$ $0$
  $- \frac{1}{3} x^{3} - \frac{4}{3} x^{2}$ $=$ $0$
  ↓
  Klammere $- \frac{1}{3} x^{2}$ aus.
  $- \frac{1}{3} x^{2} (x + 4)$ $=$ $0$
  Laut dem Satz vom Nullprodukt gibt es zwei Nullstellen: die doppelte Nullstelle $x = 0$ und die einfache Nullstelle $x = - 4$ . Beide liegen im Definitionsbereich.
  Graph zeichnen
  Du darfst nicht über die Grenzen des Definitionsbereichs hinweg zeichnen. Für ein ordentliches Ergebnis solltest du bei der Wertetabelle die Schrittweite 0,5 wählen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme zuerst die Nullstellen.
  Zeichne anschließend die Funktion:
  Beachte die Definitionsmenge und zeichne nicht über die Grenzen hinaus.
  Erstelle eine Wertetabelle im Taschenrechner und zeichne einen Punkt pro Kästchen ein.
  Beschrifte die Achsen und den Graphen.
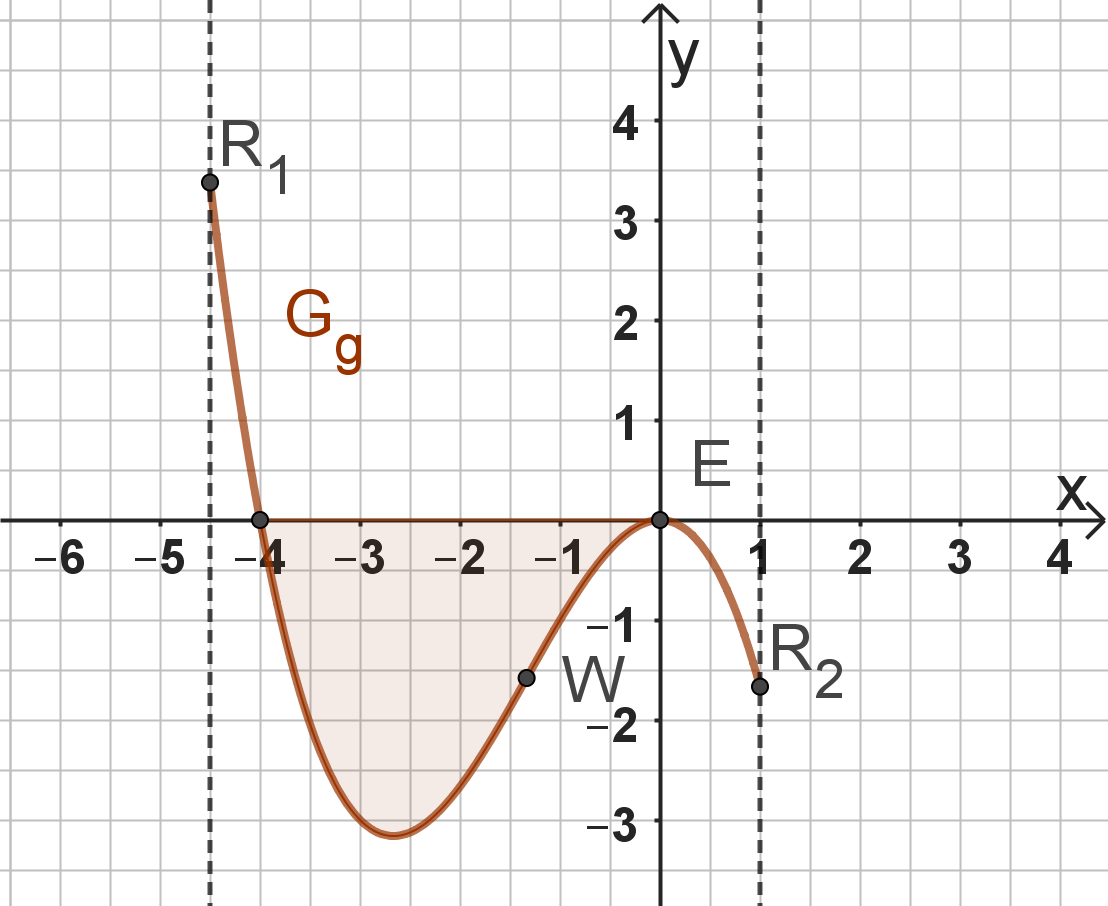
6. Der Graph der Funktion $g$ und die x-Achse schließen im III. Quadranten des Koordinatensystems ein endliches Flächenstück ein. Berechnen Sie die Maßzahl des Flächeninhalts dieses Flächenstücks. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Gesucht ist der Flächeninhalt des Flächenstücks im III. Quadranten. Das ist die Teilfläche, die durch $x = - 4$ und $x = 0$ begrenzt wird.
  Veranschaulichung der gesuchten Fläche
  Mit dem bestimmten Integral kannst du den Flächeninhalt bestimmen:
  $\int_{- 4}^{0} g (x) d x$ $=$
  ↓
  Bilde eine Stammfunktion $G$
  $=$ ${[- \frac{1}{12} x^{4} - \frac{4}{9} x^{3}]}_{- 4}^{0}$
  ↓
  Setze die Grenzen ein und subtrahiere.
  $=$ $G (0) - G (- 4)$
  $=$ $0 - \frac{64}{9}$
  $=$ $- \frac{64}{9}$
  Da das markierte Flächenstück komplett unterhalb der x-Achse liegt, entspricht der Betrag des bestimmten Integrals dem Flächeninhalt, also:
  $A = \frac{64}{9} FE$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Markiere das Flächenstück in der Zeichnung und ermittle so die Grenzen des Integrals.
  Berechne den Wert des bestimmten Integrals.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
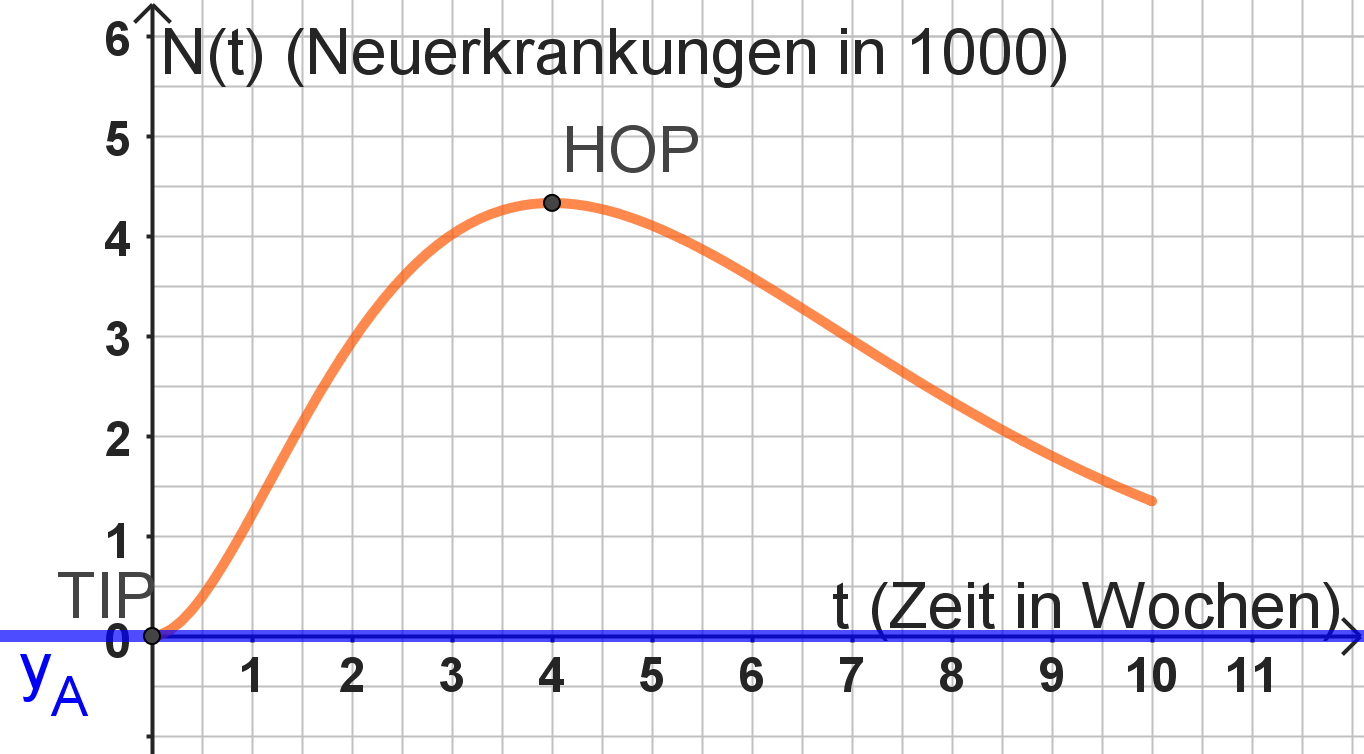
Der Verlauf der Anzahl der Neuerkrankungen für eine bestimmte Grippewelle in einer gewissen Region in Abhängigkeit von der Zeit kann vereinfacht durch die Funktion $N$ mit der Funktionsgleichung $N (t) = 2 t^{2} \cdot e^{- 0,5 t}$ mit $t \in ℝ_{0}^{+}$ beschrieben werden.
Dabei bedeutet die Variable $t$ die Zeit in Wochen ab Beginn der Grippewelle zum Zeitpunkt $t_{0} = 0$ . Der Funktionswert $N (t)$ gibt die Anzahl der an Grippe neu erkrankten Menschen in Tausend an.
Auf das Mitführen von Einheiten während der Rechnungen kann verzichtet werden. Runden Sie Ihre Ergebnisse sinnvoll.
1. Berechnen Sie, zu welchem Zeitpunkt $t_{\max}$ die Zahl der neu erkrankten Menschen ihr Maximum annimmt und berechnen Sie diese maximale Anzahl.
  [Teilergebnis: $\dot{N} (t) = (4 t - t^{2}) \cdot e^{- 0,5 t}$ ] (7 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  Ableiten
  Bestimme die 1. Ableitung von $N (t) = 2 t^{2} \cdot e^{- 0,5 t}$ mit der Produktregel und der Kettenregel.
  $N^{'} (t)$ $=$ $4 t \cdot e^{- 0,5 t} + 2 t^{2} \cdot (- 0,5) e^{- 0,5 t}$
  ↓
  Verrechne.
  $=$ $4 t \cdot e^{- 0,5 t} - t^{2} \cdot e^{- 0,5 t}$
  ↓
  Klammere $t \cdot e^{- 0,5 t}$ aus.
  $=$ $t \cdot e^{- 0,5 t} (4 - t)$
  ↓
  Reine Ästhetik:
  $=$ $t (4 - t) e^{- 0,5 t}$
  Nullstellen bestimmen
  Du suchst die Lösung der Gleichung $N^{'} (t) = 0 \Leftrightarrow t (4 - t) e^{- 0,5 t} = 0$ .
  Laut dem Satz vom Nullprodukt kann jeder Faktor einzeln betrachtet werden. Dabei ist $e^{f (x)} > 0$ für jede Funktion $f (x)$ , hat also nie den Wert 0.
  Es gibt somit die Nullstellen $t = 0$ und $t = 4$ .
  Monotonietabelle
  Lege mit diesen Werten eine Monotonietabelle an. Beachte, dass $t = 0$
  zugleich der Rand des Definitionsbereichs ist und dort ein Randextrempunkt liegt:
  t
  t=0
  0<t<4
  t=4
  t<4
  Vorzeichen $N^{'} (t)$
  0
  +
  0
  -
  Verlauf $G_{N}$
  $R T I P$
  $↗$
  $H O P$
  $↘$
  Funktionswert berechnen
  Da nur nach dem Maximum gefragt ist, musst du nur $N (4)$ bestimmen.
  $N (4) = \frac{32}{e^{2}} \approx 4,331$
  Bedeutung im Sachkontext
  Die Zahl der Neuerkrankungen ist laut Angabentext in Tausend.
  Also liegt das Maximum der neu erkrankten Menschen nach 4 Wochen bei 4331 Neuerkrankungen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Gesucht ist der Hochpunkt des Graphen $G_{N}$ .
  Bestimme die 1. Ableitung mit der Produktregel und der Kettenregel.
  Bestimme die Nullstellen der 1. Ableitung.
  Weise, zum Beispiel mit einer Monotonietabelle, nach, dass es es sich um einen Hochpunkt handelt.
  Bestimme den zugehörigen Funktionswert.
  Achte auf die Aufgabenstellung, um den Antwortsatz zu formulieren. Der Funktionswert kann nicht direkt verwendet werden.
2. Ermitteln Sie das Verhalten der Funktionswerte $N (t)$ für $t \to \infty$ und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwert bestimmen
  Bestimme $l i m_{t \to + \infty} N (t)$ :
  $\lim_{t \to + \infty} \underset{\to + \infty}{\underset{⏟}{2 t^{2}}} \cdot \underset{\to 0^{+}}{\underset{⏟}{e^{\overset{\to - \infty}{\overset{⏞}{- 0,5 t}}}}} = 0^{+}$
  Da $t$ die Zeit in Wochen beschreibt und $N (t)$ die Zahl der Neuerkrankungen, bedeutet der Grenzwert, dass sich die Zahl der Neuerkrankungen nach vielen Wochen auf 0 reduziert und es somit keine Neuerkrankungen mehr gibt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme den Grenzwert nachvollziehbar, indem du den Term geeignet in Bausteine zerlegst.
  Für die Interpretation im Sachkontext ist wichtig, für was t und N(t) steht.
3. Zeichnen Sie unter Verwendung aller bisheriger Ergebnisse und weiterer geeigneter Funktionswerte den Graphen der Funktion $N$ im Bereich $0 \leq t \leq 10$ in ein geeignetes beschriftetes Koordinatensystem. Maßstab für beide Achsen: $1 LE = 1 c m$ (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
  Die Achsen beschriftest du zum Beispiel mit $t$ und $N (t)$ .
  Für ein ordentliches Ergebnis solltest du bei der Wertetabelle die Schrittweite $0,5$ einstellen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Fertige eine Wertetabelle an.
  Vergiss nicht, die Achsen der Situation entsprechend zu beschriften.
4. Gegeben ist die Funktion $G : t \mapsto (- 4 t^{2} - 16 t - 32) \cdot e^{- 0,5 t}$ mit der Definitionsmenge $D_{G} = ℝ_{0}^{+}$ . Zeigen Sie, dass die Funktion $G$ eine mögliche Stammfunktion von $N$ ist. Berechnen Sie damit die durchschnittliche Anzahl an neu erkrankten Menschen während der ersten acht Wochen ab Beginn der Grippewelle. (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion, Integral und Flächenberechnung
  Nachweis
  Um die Ableitung zu bestimmen, brauchst du die Produktregel und die Kettenregel.
  $G^{'} (t)$ $=$ $(- 8 t - 16) \cdot e^{- 0,5 t} + (- 4 t^{2} - 16 t - 32) \cdot (- 0,5) \cdot e^{- 0,5 t}$
  $=$ $(- 8 t - 16) \cdot e^{- 0,5 t} + (2 t^{2} + 8 t + 16) \cdot e^{- 0,5 t}$
  ↓
  Klammere $e^{- 0,5 t}$ aus.
  $=$ $e^{- 0,5 t} (- 8 t - 16 + 2 t^{2} + 8 t + 16)$
  $=$ $2 t^{2} e^{- 0,5 t}$
  $=$ $N (t)$
  Und somit ist $G$ eine Stammfunktion von $N$ .
  Durchschnittliche Zahl der Neuerkrankungen
  Mit dem Integral $\int_{0}^{8} N (t) d t$ kannst du die Zahl der insgesamt erkrankten Personen in den ersten acht Wochen bestimmen. Da der Zeitraum 8 Wochen umfasst, bekommst du die Zahl der durchschnittlichen Neuerkrankungen pro Woche, indem du diesen Wert durch 8 teilst:
  $\frac{1}{8} \int_{0}^{8} N (t) d t$ $=$ $\frac{1}{8} {[G (t)]}_{0}^{8}$
  $=$ $\frac{1}{8} (G (8) - G (0))$
  $=$ $\frac{1}{8} (- \frac{416}{e^{4}} - (- 32))$
  $\approx$ $\frac{1}{8} \cdot 24,38$
  $\approx$ $3,048$
  In den ersten acht Wochen gab es durchschnittlich 3048 Neuerkrankungen pro Woche.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bilde die Ableitung von G und zeige somit, dass $G^{'} (t) = N (t)$ .
  Der Wert des bestimmten Integrals $\int_{0}^{8} N (t) d t$ gibt die insgesamte Zahl neu erkrankter Menschen in den ersten acht Wochen an.
  Diesen Wert musst du noch zu einem wöchentlichen Durchschnittswert machen.

t	t=0	0<t<4	t=4	t<4
Vorzeichen $N^{'} (t)$	0	+	0	-
Verlauf $G_{N}$	$R T I P$	$↗$	$H O P$	$↘$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$27 a - 6 \cdot (- \frac{4}{3})$	$=$	$- 1$
$27 a + 8$	$=$	$- 1$	$- 8$
$27 a$	$=$	$- 9$	$: 27$
$a$	$=$	$- \frac{1}{3}$

$g^{'} (x)$	$=$	$0$
$- x^{2} - \frac{8}{3} x$	$=$	$0$
	↓	Klammere $- x$ aus.
$- x (x + \frac{8}{3})$	$=$	$0$

$g^{''} (x)$	$=$	$0$
$- 2 x - \frac{8}{3}$	$=$	$0$	$+ \frac{8}{3}$
$- 2 x$	$=$	$\frac{8}{3}$	$: (- 2)$
$x$	$=$	$- \frac{4}{3}$

$g (x)$	$=$	$0$
$- \frac{1}{3} x^{3} - \frac{4}{3} x^{2}$	$=$	$0$
	↓	Klammere $- \frac{1}{3} x^{2}$ aus.
$- \frac{1}{3} x^{2} (x + 4)$	$=$	$0$

$\int_{- 4}^{0} g (x) d x$	$=$
	↓	Bilde eine Stammfunktion $G$
	$=$	${[- \frac{1}{12} x^{4} - \frac{4}{9} x^{3}]}_{- 4}^{0}$
	↓	Setze die Grenzen ein und subtrahiere.
	$=$	$G (0) - G (- 4)$
	$=$	$0 - \frac{64}{9}$
	$=$	$- \frac{64}{9}$

$N^{'} (t)$	$=$	$4 t \cdot e^{- 0,5 t} + 2 t^{2} \cdot (- 0,5) e^{- 0,5 t}$
	↓	Verrechne.
	$=$	$4 t \cdot e^{- 0,5 t} - t^{2} \cdot e^{- 0,5 t}$
	↓	Klammere $t \cdot e^{- 0,5 t}$ aus.
	$=$	$t \cdot e^{- 0,5 t} (4 - t)$
	↓	Reine Ästhetik:
	$=$	$t (4 - t) e^{- 0,5 t}$

$G^{'} (t)$	$=$	$(- 8 t - 16) \cdot e^{- 0,5 t} + (- 4 t^{2} - 16 t - 32) \cdot (- 0,5) \cdot e^{- 0,5 t}$
	$=$	$(- 8 t - 16) \cdot e^{- 0,5 t} + (2 t^{2} + 8 t + 16) \cdot e^{- 0,5 t}$
	↓	Klammere $e^{- 0,5 t}$ aus.
	$=$	$e^{- 0,5 t} (- 8 t - 16 + 2 t^{2} + 8 t + 16)$
	$=$	$2 t^{2} e^{- 0,5 t}$
	$=$	$N (t)$

$\frac{1}{8} \int_{0}^{8} N (t) d t$	$=$	$\frac{1}{8} {[G (t)]}_{0}^{8}$
	$=$	$\frac{1}{8} (G (8) - G (0))$
	$=$	$\frac{1}{8} (- \frac{416}{e^{4}} - (- 32))$
	$\approx$	$\frac{1}{8} \cdot 24,38$
	$\approx$	$3,048$

Teil 2, Analysis I

Hast du eine Frage oder Feedback?

allgemeiner Funktionsterm

Bedingungsgleichungen

Gleichungssystem lösen

Hast du eine Frage oder Feedback?

Randextrempunkte

Weitere Extrempunkte

Wertemenge

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Nullstellen bestimmen

Graph zeichnen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Ableiten

Nullstellen bestimmen

Monotonietabelle

Funktionswert berechnen

Bedeutung im Sachkontext

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Nachweis

Durchschnittliche Zahl der Neuerkrankungen

Hast du eine Frage oder Feedback?