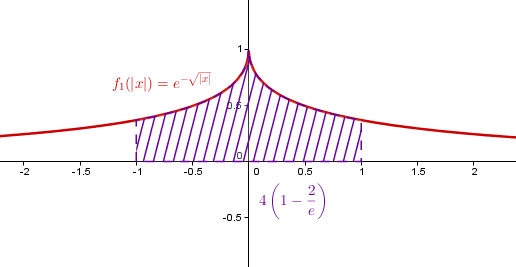
Es ist folgende Funktionenschar gegeben:
In den Teilaufgaben findest du vieles, das du für diese Funktion berechnen kannst.
Suche dir heraus, was du üben möchtest.
Die Teilaufgaben sind in einer logischen Reihenfolge angeordnet, daher wird in späteren Aufgaben auf Ergebnisse von früher zurückgegriffen.
Wenn dir nicht klar ist, woher diese Ergebnisse kommen, dann rechne am besten die zugehörige Teilaufgabe davor nach.
Definitionsbereich bestimmen
Grenzwertbetrachtungen: Bestimme die Grenzwerte an allen Grenzen des Definitionsbereichs.
Asymptoten bestimmen
Nullstellen bestimmen
Symmetrieverhalten überprüfen
Monotonieverhalten bestimmen
Krümmungsverhalten bestimmen
Extremwerte bestimmen
Wertebereich bestimmen
Tangente bestimmen:
Bestimme die Tangente an den Funktionsgraphen von , die für auch durch den Punkt geht und für durch den Punkt .
Stammfunktion I:
Zeige, dass
eine Stammfunktion von für ist.
Stammfunktion II:
Bestimme durch Rechnung die Stammfunktion von .
Achtung, diese Integration ist etwas schwieriger und erfordert mehr Überlegungen und Rechenschritte, als in der Schule normalerweise verlangt werden. Wer allerdings ein paar Tricks beim Integrieren ausprobieren/lernen will kann die Aufgabe gerne bearbeiten oder sich die Lösung anschauen.
Für alle Anderen reicht es, die Aufgabe "Stammfunktion I" zu bearbeiten, die normalem Schulniveau entspricht.
Flächenberechnung I:
Berechne die Fläche, die der Funktionsgraph mit den Koordinatenachsen einschließt.
Flächenberechnung II:
Berechne die Fläche die von der x-Achse, den Geraden und dem Graphen von eingeschlossen wird.
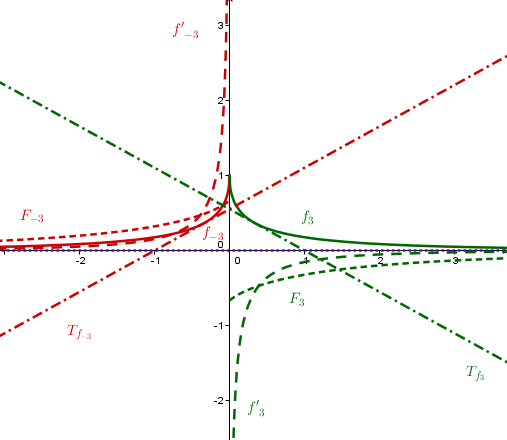
Graphen zeichnen:
Zeichne folgende Graphen für in ein oder mehrere Koordinatensysteme:
mit seinen Asymptoten und
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?