Aufgaben zum Belegen von Termvariablen

Hier findest du Übungsaufgaben zum Arbeiten mit Variablen. Lerne, Variablen zum Einsetzen von Werten zu verwenden!

1
Berechne den Wert des Terms $T (a) = 3 \cdot (8 a) + 4$ , wenn a = 2 ist.
52
60
45
51
Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt vor Strich
Ersetze $a$ durch $2$ im Term $T (a) = 3 \cdot (8 a) + 4$ . Du erhältst:
$3 \cdot (8 \cdot 2) + 4$
Weil Punkt vor Strich gilt, rechnest du nach der Klammer das Ergebnis der Klammer mal 3 und dann erst plus 4.
$\begin{array}{l} 3 \cdot 16 + 4 \\ = 48 + 4 \\ = 52 \end{array}$

Setze in den Term $a^{2} - 2 ab + \frac{3}{4} a$ die angegebenen Werte für $a$ und $b$ ein und berechne die zugehörigen Termwerte.

$a = - 2$ , $b = 1$

$a = - 1$ , $b = 0$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Terme umformen
Setze $a = - 1$ ein.
$a^{2} - 2 ab + \frac{3}{4} a$ $=$ ${(- 1)}^{2} - 2 \cdot (- 1) \cdot b + \frac{3}{4} \cdot (- 1)$
↓
Setze $b = 0$ ein.
$=$ ${(- 1)}^{2} - 2 \cdot (- 1) \cdot 0 + \frac{3}{4} \cdot (- 1)$
↓
Ausmultiplizieren.
$=$ $1 - 0 + (- \frac{3}{4})$
$=$ $1 - \frac{3}{4}$
$=$ $\frac{1}{4}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$a = - \frac{1}{2}$ ; $b = - 2$

$a = - \frac{1}{4}$ , $b = 0,25$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Terme umformen
Setze $a = - \frac{1}{4}$ ein.
$a^{2} - 2 ab + \frac{3}{4} a$ $=$ ${(- \frac{1}{4})}^{2} - 2 \cdot (- \frac{1}{4}) \cdot b + \frac{3}{4} \cdot (- \frac{1}{4})$
↓
$b = 0,25$ einsetzen. Beachte 0,25 = $\frac{1}{4}$ .
$=$ ${(- \frac{1}{4})}^{2} - 2 \cdot (- \frac{1}{4}) \cdot (\frac{1}{4}) + \frac{3}{4} \cdot (- \frac{1}{4})$
↓
Ausmultiplizieren.
$=$ $\frac{1}{16} - (- \frac{2}{16}) + (- \frac{3}{16})$
$=$ $\frac{1}{16} + \frac{2}{16} - \frac{3}{16}$
$=$ $0$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$a = 0$ , $b = - \frac{7}{13}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Terme umformen
Setze $a = 0$ ein.
$a^{2} - 2 ab + \frac{3}{4} a$ $=$ $0^{2} - 2 \cdot 0 \cdot b + \frac{3}{4} \cdot 0$
↓
Da durch das Multiplizieren mit 0, der gesamte Term gleich 0 ist, muss $b$ nicht mehr eingesetzt werden.
$=$ $0 - 0 + 0$
$=$ $0$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$a = 0,5$ , $b = - \frac{1}{3}$

Setze in den Term $T (x) = (\frac{1}{4} - x + x^{2}) : (- \frac{1}{2})$ für die Variable $x$ die Zahlen $- 2; - 1; - 0,50; 0,25;$ $\frac{3}{4}$ sowie $1$ ein und berechne die zugehörigen Termwerte.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Terme und Variablen

$x$	-2	-1	-0,5	0,25	$\frac{3}{4}$	1
$T (x)$	-12,5	-4,5	-2	-0,125	-0,125	-0,5

für $x = - 2$

$(\frac{1}{4} - x + x^{2}) : (- \frac{1}{2})$	$=$
	↓	$x = - 2$ einsetzen
$(\frac{1}{4} - (- 2) + {(- 2)}^{2}) : (- \frac{1}{2})$	$=$
$(\frac{1}{4} + 2 + 4) : (- \frac{1}{2})$	$=$
	↓	Hauptnenner bilden $\to 4$
$(\frac{1}{4} + \frac{8}{4} + \frac{16}{4}) : (- \frac{1}{2})$	$=$
$\frac{25}{4} : (- \frac{1}{2})$	$=$
	↓	Mit dem Kehrwert multiplizieren
$\frac{25}{4} \cdot (- \frac{2}{1})$	$=$
$\frac{25}{4} \cdot (- \frac{2}{1})$	$=$
$- \frac{25}{2}$	$=$	$- 12,5$

für $x = - 1$

$(\frac{1}{4} - x + x^{2}) : (- \frac{1}{2})$	$=$
	↓	$x = - 1$ einsetzen
$(\frac{1}{4} - (- 1) + {(- 1)}^{2}) : (- \frac{1}{2})$	$=$
$(\frac{1}{4} + 1 + 1) : (- \frac{1}{2})$	$=$
	↓	Hauptnenner bilden $\to 4$
$(\frac{1}{4} + \frac{4}{4} + \frac{4}{4}) : (- \frac{1}{2})$	$=$
	↓	Mit dem Kehrwert multiplizieren
$\frac{9}{4} \cdot (- \frac{2}{1})$	$=$
$- \frac{9}{2}$	$=$	$- 4,5$

für $x = - 0,5$

$(\frac{1}{4} - x + x^{2}) : (- \frac{1}{2})$	$=$
$(\frac{1}{4} - (- 0,5) + {(- 0,5)}^{2}) : (- \frac{1}{2})$	$=$
$(\frac{1}{4} + 0,5 + 0,25) : (- \frac{1}{2})$	$=$
$(\frac{1}{4} + \frac{2}{4} + \frac{1}{4}) : (- \frac{1}{2})$	$=$
$\frac{4}{4} \cdot (- \frac{2}{1})$	$=$
$- \frac{4}{2}$	$=$	$- 2$

für $x = 0,25$

$(\frac{1}{4} - x + x^{2}) : (- \frac{1}{2})$	$=$
$(\frac{1}{4} - (0,25) + {(0,25)}^{2}) : (- \frac{1}{2})$	$=$
$(\frac{1}{4} - 0,25 + 0,0625) : (- \frac{1}{2})$	$=$
$(\frac{1}{4} - \frac{1}{4} + 0,0625) : (- \frac{1}{2})$	$=$
$(\frac{1}{16}) : (- \frac{1}{2})$	$=$
$(\frac{1}{16}) \cdot (- \frac{2}{1})$	$=$
$(- \frac{1}{8})$	$=$	$- 0,125$

für $x = \frac{3}{4}$

$(\frac{1}{4} - x + x^{2}) : (- \frac{1}{2})$	$=$
$(\frac{1}{4} - (\frac{3}{4}) + {(\frac{3}{4})}^{2}) : (- \frac{1}{2})$	$=$
$(\frac{1}{4} - \frac{3}{4} + \frac{9}{16}) : (- \frac{1}{2})$	$=$
$(\frac{4}{16} - \frac{12}{16} + \frac{9}{16}) : (- \frac{1}{2})$	$=$
$\frac{1}{16} \cdot (- \frac{2}{1})$	$=$
$(- \frac{1}{8})$	$=$	$- 0,125$

für $x = 1$

$(\frac{1}{4} - x + x^{2}) : (- \frac{1}{2})$	$=$
$(\frac{1}{4} - 1 + {(1)}^{2}) : (- \frac{1}{2})$	$=$
$(\frac{1}{4}) : (- \frac{1}{2})$	$=$
$\frac{1}{4} \cdot (- \frac{2}{1})$	$=$	$- 0,5$

Gegeben sind die Terme

$T_{1} (x) = {(\frac{3 - x}{2})}^{2}$ ,

$T_{2} (x) = \frac{{(3 - x)}^{2}}{2}$ ,

$T_{3} (x) = \frac{3 - x^{2}}{2}$ ,

$T_{4} (x) = 3 - \frac{x^{2}}{2}$ und

$T_{5} (x) = 3 - {(\frac{x}{2})}^{2}$ .

Setze in die Terme jeweils für $x$ die Zahlen $- 2; 0; 1,5$ sowie $3 \frac{1}{3}$ ein und trage die Termwerte in einer Tabelle zusammen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechnen mit Bruchtermen

	$- 2$	$0$	$1,5$	$3 \frac{1}{3}$
$T_{1}$	$6 \frac{1}{4}$	$2 \frac{1}{4}$	$\frac{9}{16}$	$\frac{1}{36}$
$T_{2}$	$12 \frac{1}{2}$	$4 \frac{1}{2}$	$1 \frac{1}{8}$	$\frac{1}{18}$
$T_{3}$	$- \frac{1}{2}$	$1 \frac{1}{2}$	$\frac{3}{8}$	$- 4 \frac{1}{18}$
$T_{4}$	$1$	$3$	$1 \frac{7}{8}$	$- 2 \frac{5}{9}$
$T_{5}$	$2$	$3$	$2 \frac{7}{16}$	$\frac{2}{9}$

Lösung für $T_{1}$

$T_{1} (x)$	$=$	${(\frac{3 - x}{2})}^{2}$
	↓	Setze $x = - 2$ ein.
$T_{1} (- 2)$	$=$	${(\frac{3 - (- 2)}{2})}^{2}$
	↓	Fasse zusammen.
	$=$	${(\frac{5}{2})}^{2}$
	↓	Potenziere den Bruch.
	$=$	$\frac{25}{4}$
	↓	Schreibe als gemischten Bruch.
	$=$	$6 \frac{1}{4}$

$T_{1} (x)$	$=$	${(\frac{3 - x}{2})}^{2}$
	↓	Setze $x = 0$ ein.
$T_{1} (0)$	$=$	${(\frac{3 - 0}{2})}^{2}$
	↓	Fasse zusammen.
	$=$	${(\frac{3}{2})}^{2}$
	↓	Potenziere den Bruch.
	$=$	$\frac{9}{4}$
	↓	Schreibe als gemischten Bruch.
	$=$	$2 \frac{1}{4}$

$T_{1} (x)$	$=$	${(\frac{3 - x}{2})}^{2}$
	↓	Setze $x = 1,5$ ein.
$T_{1} (1,5)$	$=$	${(\frac{3 - 1,5}{2})}^{2}$
	↓	Fasse zusammen.
	$=$	${(\frac{1,5}{2})}^{2}$
	↓	Erweitere den Bruch mit $2$ .
	$=$	${(\frac{3}{4})}^{2}$
	↓	Potenziere den Bruch.
	$=$	$\frac{9}{16}$

$T_{1} (x)$	$=$	${(\frac{3 - x}{2})}^{2}$
	↓	Setze $x = 3 \frac{1}{3}$ ein.
$T_{1} (3 \frac{1}{3})$	$=$	${(\frac{3 - 3 \frac{1}{3}}{2})}^{2}$
	↓	Fasse zusammen.
	$=$	${(\frac{- \frac{1}{3}}{2})}^{2}$
	↓	Teile den Bruch $- \frac{1}{3}$ durch $2$ .
	$=$	${(- \frac{1}{6})}^{2}$
	↓	Potenziere den Bruch.
	$=$	$\frac{1}{36}$

Lösung für $T_{2}$

$T_{2} (x)$	$=$	$\frac{(3 - x)^{2}}{2}$
	↓	Setze $x = - 2$ ein.
$T_{2} (- 2)$	$=$	$\frac{(3 - (- 2))^{2}}{2}$
	↓	Fasse zusammen.
	$=$	$\frac{5^{2}}{2}$
	↓	Vereinfache.
	$=$	$\frac{25}{2}$
	↓	Schreibe als gemischten Bruch.
	$=$	$12 \frac{1}{2}$

$T_{2} (x)$	$=$	$\frac{(3 - x)^{2}}{2}$
	↓	Setze $x = 0$ ein.
$T_{2} (0)$	$=$	$\frac{(3 - 0)^{2}}{2}$
	↓	Fasse zusammen.
	$=$	$\frac{3^{2}}{2}$
	↓	Vereinfache.
	$=$	$\frac{9}{2}$
	↓	Schreibe als gemischten Bruch.
	$=$	$4 \frac{1}{2}$

$T_{2} (x)$	$=$	$\frac{(3 - x)^{2}}{2}$
	↓	Setze $x = 1,5$ ein.
$T_{2} (1,5)$	$=$	$\frac{(3 - 1,5)^{2}}{2}$
	↓	Fasse zusammen.
	$=$	$\frac{{(\frac{3}{2})}^{2}}{2}$
	↓	Berechne das Quadrat.
	$=$	$\frac{(\frac{9}{4})}{2}$
	↓	Teile den Bruch $\frac{9}{4}$ durch $2$ .
	$=$	$\frac{9}{8}$
	↓	Schreibe als gemischten Bruch.
	$=$	$1 \frac{1}{8}$

$T_{2} (x)$	$=$	$\frac{(3 - x)^{2}}{2}$
	↓	Setze $x = 3 \frac{1}{3}$ ein.
$T_{2} (3 \frac{1}{3})$	$=$	$\frac{{(3 - 3 \frac{1}{3})}^{2}}{2}$
	↓	Fasse zusammen.
	$=$	$\frac{{(- \frac{1}{3})}^{2}}{2}$
	↓	Berechne das Quadrat.
	$=$	$\frac{(\frac{1}{9})}{2}$
	↓	Teile den Bruch $\frac{1}{9}$ durch $2$ .
	$=$	$\frac{1}{18}$

Lösung für $T_{3}$

$T_{3} (x)$	$=$	$\frac{3 - x^{2}}{2}$
	↓	Setze $x = - 2$ ein.
$T_{3} (- 2)$	$=$	$\frac{3 - (- 2)^{2}}{2}$
	↓	Berechne das Quadrat.
	$=$	$\frac{3 - 4}{2}$
	↓	Vereinfache.
	$=$	$- \frac{1}{2}$

$T_{3} (x)$	$=$	$\frac{3 - x^{2}}{2}$
	↓	Setze $x = 0$ ein.
$T_{3} (0)$	$=$	$\frac{3 - 0^{2}}{2}$
	↓	Vereinfache.
	$=$	$\frac{3}{2}$
	↓	Schreibe als gemischten Bruch.
	$=$	$1 \frac{1}{2}$

$T_{3} (x)$	$=$	$\frac{3 - x^{2}}{2}$
	↓	Setze $x = 1,5$ ein.
$T_{3} (1,5)$	$=$	$\frac{3 - {1,5}^{2}}{2}$
	↓	Berechne das Quadrat
	$=$	$\frac{3 - 2,25}{2}$
	$=$	$\frac{0,75}{2}$
	↓	Erweitere den Bruch mit $4$ .
	$=$	$\frac{3}{8}$

$T_{3} (x)$	$=$	$\frac{3 - x^{2}}{2}$
	↓	Setze $x = 3 \frac{1}{3}$ ein.
$T_{3} (3 \frac{1}{3})$	$=$	$\frac{3 - {(3 \frac{1}{3})}^{2}}{2}$
	↓	Wandle den gemischten Bruch um.
	$=$	$\frac{3 - {(\frac{10}{3})}^{2}}{2}$
	↓	Berechne das Quadrat.
	$=$	$\frac{3 - (\frac{100}{9})}{2}$
	↓	Wandle $3$ in Neuntel um.
	$=$	$\frac{\frac{27}{9} - \frac{100}{9}}{2}$
	↓	Berechne die Differenz.
	$=$	$\frac{- \frac{73}{9}}{2}$
	↓	Teile den Bruch $- \frac{73}{9}$ durch $2$ .
	$=$	$- \frac{73}{18}$
	↓	Schreibe als gemischten Bruch.
	$=$	$- 4 \frac{1}{18}$

Lösung für $T_{4}$

$T_{4} (x)$	$=$	$3 - \frac{x^{2}}{2}$
	↓	Setze $x = - 2$ ein.
$T_{4} (- 2)$	$=$	$3 - \frac{(- 2)^{2}}{2}$
	↓	Berechne das Quadrat.
	$=$	$3 - \frac{4}{2}$
	↓	Vereinfache.
	$=$	$3 - 2$
	↓	Vereinfache.
	$=$	$1$

$T_{4} (x)$	$=$	$3 - \frac{x^{2}}{2}$
	↓	Setze $x = 0$ ein.
$T_{4} (0)$	$=$	$3 - \frac{0^{2}}{2}$
	↓	Vereinfache.
	$=$	$3 - 0$
	↓	Vereinfache.
	$=$	$3$

$T_{4} (x)$	$=$	$3 - \frac{x^{2}}{2}$
	↓	Setze $x = 1,5$ ein.
$T_{4} (1,5)$	$=$	$3 - \frac{{1,5}^{2}}{2}$
	↓	Berechne das Quadrat.
	$=$	$3 - \frac{2,25}{2}$
	↓	Erweitere den Bruch $\frac{2,25}{2}$ mit $4$ .
	$=$	$3 - \frac{9}{8}$
	↓	Wandle $3$ in Achtel um.
	$=$	$\frac{24}{8} - \frac{9}{8}$
	↓	Berechne die Differenz.
	$=$	$\frac{15}{8}$
	↓	Schreibe als gemischten Bruch.
	$=$	$1 \frac{7}{8}$

$T_{4} (x)$	$=$	$3 - \frac{x^{2}}{2}$
	↓	Setze $x = 3 \frac{1}{3}$ ein.
$T_{4} (3 \frac{1}{3})$	$=$	$3 - \frac{{(3 \frac{1}{3})}^{2}}{2}$
	↓	Wandle den gemischten Bruch um.
	$=$	$3 - \frac{{(\frac{10}{3})}^{2}}{2}$
	↓	Berechne das Quadrat.
	$=$	$3 - \frac{(\frac{100}{9})}{2}$
	↓	Teile den Bruch $\frac{100}{9}$ durch $2$ .
	$=$	$3 - \frac{100}{18}$
	↓	Wandle $3$ in Achtzehntel um.
	$=$	$\frac{54}{18} - \frac{100}{18}$
	↓	Berechne die Differenz.
	$=$	$- \frac{46}{18}$
	↓	Kürze.
	$=$	$- \frac{23}{9}$
	↓	Schreibe als gemischten Bruch.
	$=$	$- 2 \frac{5}{9}$

Lösung für $T_{5}$

$T_{5} (x)$	$=$	$3 - {(\frac{x}{2})}^{2}$
	↓	Setze $x = - 2$ ein.
$T_{5} (- 2)$	$=$	$3 - {(\frac{- 2}{2})}^{2}$
	↓	Kürze den Bruch.
	$=$	$3 - (- 1)^{2}$
	↓	Berechne das Quadrat.
	$=$	$3 - 1$
	↓	Vereinfache.
	$=$	$2$

$T_{5} (x)$	$=$	$3 - {(\frac{x}{2})}^{2}$
	↓	Setze $x = 0$ ein.
$T_{5} (0)$	$=$	$3 - {(\frac{0}{2})}^{2}$
	↓	Berechne den Bruch.
	$=$	$3 - 0$
	↓	Vereinfache.
	$=$	$3$

$T_{5} (x)$	$=$	$3 - {(\frac{x}{2})}^{2}$
	↓	Setze $x = 1,5$ ein.
$T_{5} (1,5)$	$=$	$3 - {(\frac{1,5}{2})}^{2}$
	↓	Berechne das Quadrat.
	$=$	$3 - \frac{2,25}{4}$
	↓	Erweitere den Bruch $\frac{2,25}{4}$ mit $4$ .
	$=$	$3 - \frac{9}{16}$
	↓	Wandle $3$ in Sechzehntel um.
	$=$	$\frac{48}{16} - \frac{9}{16}$
	↓	Berechne die Differenz.
	$=$	$\frac{39}{16}$
	↓	Schreibe als gemischten Bruch.
	$=$	$2 \frac{7}{16}$

$T_{5} (x)$	$=$	$3 - {(\frac{x}{2})}^{2}$
	↓	Setze $x = 3 \frac{1}{3}$ ein.
$T_{5} (3 \frac{1}{3})$	$=$	$3 - {(\frac{3 \frac{1}{3}}{2})}^{2}$
	↓	Wandle den gemischten Bruch um.
	$=$	$3 - {(\frac{\frac{10}{3}}{2})}^{2}$
	↓	Teile den Bruch $\frac{10}{3}$ durch $2$ .
	$=$	$3 - {(\frac{10}{6})}^{2}$
	↓	Berechne das Quadrat.
	$=$	$3 - \frac{100}{36}$
	↓	Wandle $3$ in Sechsunddreißigstel um.
	$=$	$\frac{108}{36} - \frac{100}{36}$
	↓	Berechne die Differenz.
	$=$	$\frac{8}{36}$
	↓	Kürze.
	$=$	$\frac{2}{9}$

Gegeben ist der Term $T (x) = - \frac{1}{2} x + 5$ . Setze für $x$ die Werte $1; 2; 2,5;$ $3 \frac{1}{3}$ $; 6; 8$ ein und trage die Termwerte in einer Tabelle zusammen. Der Tabelle kannst du Wertepaare $(x | T (x))$ , z. B. $(2 | T (2))$ , entnehmen und als Koordinaten des Punktes $(2 | 4)$ deuten.

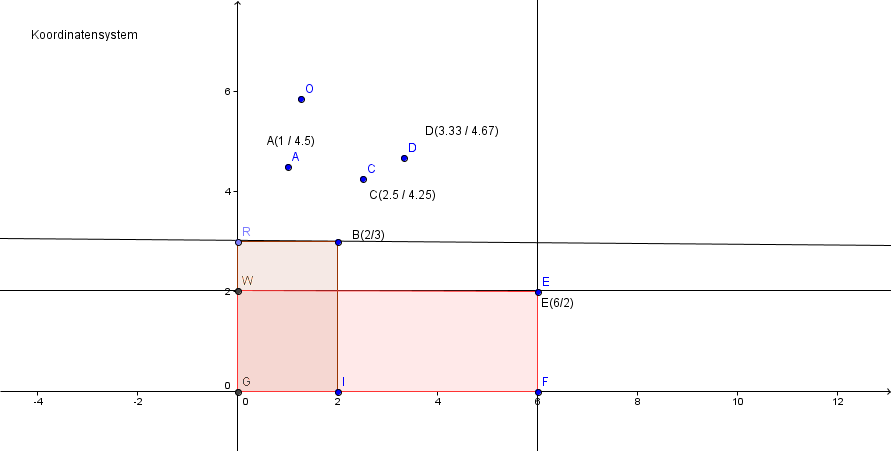
Trage für die Wertepaare aus der Tabelle die zugehörigen Punkte in ein Koordinatensystem ein.

Tabelle
$1$
$2$
$2,5$
$3 \frac{1}{3}$
$6$
$8$
$T (x) = - \frac{1}{2} x + 5$
$4,5$
$4$
$4 \frac{1}{4}$
$4 \frac{2}{3}$
$2$
$1$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

	$1$	$2$	$2,5$	$3 \frac{1}{3}$	$6$	$8$
$T (x) = - \frac{1}{2} x + 5$	$4,5$	$4$	$4 \frac{1}{4}$	$4 \frac{2}{3}$	$2$	$1$

Zeichne vom Punkt $(2 | T (2))$ die Lote auf die $x$ - und $y$ -Achse; es entsteht ein Rechteck. Zeichne auch für den Punkt $(6 | T (6))$ das entsprechende Rechteck ein. Suche den Wert für $x$ , bei dem das zu $(x | T (x))$ gehörende Rechteck einen möglichst großen Flächeninhalt hat.

6
Gegeben ist der Term $T (x) = \frac{5 - 2 x}{x - 3}$ .
1. Erstelle eine Tabelle für die Werte von $x$ und $T (x)$ . Setze für $x$ die folgenden Werte in die Tabelle ein: $- 4,5$ ; $- 4$ ; $- \frac{3}{2}$ ; $0$ ; $1$ ; $2 \frac{1}{2}$ ; $3 \frac{1}{3}$ ; $4$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Term
  Setze in $T (x) = \frac{5 - 2 x}{x - 3}$ die Werte
  $x = - 4,5$
  $x = - 4$
  $x = - \frac{3}{2}$
  $x = 0$
  $x = 1$
  $x = 2 \frac{1}{2}$
  $x = 3 \frac{1}{3}$
  $x = 4$
  ein.
  $x$
  $- 4,5$
  $- 4$
  $- \frac{3}{2}$
  $0$
  $1$
  $2 \frac{1}{2}$
  $3 \frac{1}{3}$
  $4$
  $T (x)$
  $- \frac{28}{15}$
  $- \frac{13}{7}$
  $- \frac{16}{9}$
  $- \frac{5}{3}$
  $- \frac{3}{2}$
  $0$
  $- 5$
  $- 3$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Beschreibe, was für ein Problem an der Stelle $x = 3$ auftritt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Term
  $T (x) = \frac{5 - 2 x}{x - 3}$
  Wenn du $x = 3$ in den Term $T (x)$ einsetzt, erhältst du den Nenner $3 - 3 = 0$ . Da jedoch nie durch $0$ geteilt werden darf, ist der Term $T (x)_{}$ für $x = 3$ nicht definiert.
  Der Term $T (x)$ hat also eine Defintionslücke an der Stelle $x = 3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

$x$	$- 4,5$	$- 4$	$- \frac{3}{2}$	$0$	$1$	$2 \frac{1}{2}$	$3 \frac{1}{3}$	$4$
$T (x)$	$- \frac{28}{15}$	$- \frac{13}{7}$	$- \frac{16}{9}$	$- \frac{5}{3}$	$- \frac{3}{2}$	$0$	$- 5$	$- 3$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

${(- 2)}^{2} - 2 \cdot (- 2) \cdot 1 + \frac{3}{4} \cdot (- 2)$	$=$	$4 - (- 4) + (- \frac{6}{4})$
	↓	Löse die Klammern auf.
	$=$	$4 + 4 - \frac{6}{4}$
	↓	Rechne $4 + 4$ aus und kürze den Bruch $\frac{6}{4}$ mit $2$ .
	$=$	$8 - \frac{3}{2}$
	↓	Denke dir $8$ als $\frac{8}{1}$ , und erweitere auf den Hauptnenner $2$ .
	$=$	$\frac{16}{2} - \frac{3}{2}$
	$=$	$\frac{13}{2}$
	$=$	$6 \frac{1}{2}$
	$=$	$6,5$

$x \cdot (- \frac{1}{2} x + 5)$	$=$	$- \frac{1}{2} (x^{2} - 10 x) + 0$
	↓	Ergänze mit ${(\frac{10}{2})}^{2} = 25$ .
	$=$	$- \frac{1}{2} (x^{2} - 10 x + 25 - 25) + 0$
	↓	Fasse mit der Bionomischen Minusformel zusammen.
	$=$	$- \frac{1}{2} ({(x - 5)}^{2} - 25) + 0$
	↓	Multipliziere teilweise aus.
	$=$	$- \frac{1}{2} {(x - 5)}^{2} + 12,5$

Aufgaben zum Belegen von Termvariablen

Variablen belegen und Termwert berechnen

Teil 1: Variablen belegen

Teil 2: Termwert berechnen

Ergebnis:

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

für $x = - 2$

für $x = - 1$

für $x = - 0,5$

für $x = 0,25$

für $x = \frac{3}{4}$

für $x = 1$

Lösung für $T_{1}$

Lösung für $T_{2}$

Lösung für $T_{3}$

Lösung für $T_{4}$

Lösung für $T_{5}$

Tabelle

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

$a^{2} - 2 ab + \frac{3}{4} a$	$=$	${(- 1)}^{2} - 2 \cdot (- 1) \cdot b + \frac{3}{4} \cdot (- 1)$
	↓	Setze $b = 0$ ein.
	$=$	${(- 1)}^{2} - 2 \cdot (- 1) \cdot 0 + \frac{3}{4} \cdot (- 1)$
	↓	Ausmultiplizieren.
	$=$	$1 - 0 + (- \frac{3}{4})$
	$=$	$1 - \frac{3}{4}$
	$=$	$\frac{1}{4}$

$a^{2} - 2 ab + \frac{3}{4} a$	$=$	${(- \frac{1}{2})}^{2} - 2 \cdot (- \frac{1}{2}) \cdot b + \frac{3}{4} \cdot (- \frac{1}{2})$
	↓	Setze $b = - 2$ ein.
	$=$	${(- \frac{1}{2})}^{2} - 2 \cdot (- \frac{1}{2}) \cdot (- 2) + \frac{3}{4} \cdot (- \frac{1}{2})$
	↓	Ausmultiplizieren.
	$=$	$\frac{1}{4} - 2 + (- \frac{3}{8})$
	↓	Hauptnenner bilden. Alle Nenner auf 8 erweitern.
	$=$	$\frac{2}{8} - \frac{16}{8} - \frac{3}{8}$
	$=$	$- \frac{17}{8}$
	$=$	$- 2 \frac{1}{8}$

$a^{2} - 2 ab + \frac{3}{4} a$	$=$	${(- \frac{1}{4})}^{2} - 2 \cdot (- \frac{1}{4}) \cdot b + \frac{3}{4} \cdot (- \frac{1}{4})$
	↓	$b = 0,25$ einsetzen. Beachte 0,25 = $\frac{1}{4}$ .
	$=$	${(- \frac{1}{4})}^{2} - 2 \cdot (- \frac{1}{4}) \cdot (\frac{1}{4}) + \frac{3}{4} \cdot (- \frac{1}{4})$
	↓	Ausmultiplizieren.
	$=$	$\frac{1}{16} - (- \frac{2}{16}) + (- \frac{3}{16})$
	$=$	$\frac{1}{16} + \frac{2}{16} - \frac{3}{16}$
	$=$	$0$

$a^{2} - 2 ab + \frac{3}{4} a$	$=$	$0^{2} - 2 \cdot 0 \cdot b + \frac{3}{4} \cdot 0$
	↓	Da durch das Multiplizieren mit 0, der gesamte Term gleich 0 ist, muss $b$ nicht mehr eingesetzt werden.
	$=$	$0 - 0 + 0$
	$=$	$0$

$a^{2} - 2 a b + \frac{3}{4} a$	$=$	${(\frac{1}{2})}^{2} - 2 \cdot \frac{1}{2} \cdot b + \frac{3}{4} \cdot \frac{1}{2}$
	↓	$b = - \frac{1}{3}$ einsetzen.
	$=$	${(\frac{1}{2})}^{2} - 2 \cdot \frac{1}{2} \cdot (- \frac{1}{3}) + \frac{3}{4} \cdot \frac{1}{2}$
	↓	Ausmultiplizieren.
	$=$	$\frac{1}{4} - 1 \cdot (- \frac{1}{3}) + \frac{3}{4} \cdot \frac{1}{2}$
	↓	Multiplikation der beiden Brüche.
	$=$	$\frac{1}{4} - (- \frac{1}{3}) + \frac{3}{8}$
	$=$	$\frac{1}{4} + \frac{1}{3} + \frac{3}{8}$
	↓	Gemeinsamen Hauptnenner bilden. Alle Brüche auf 24 im Nenner erweitern.
	$=$	$\frac{6}{24} + \frac{8}{24} + \frac{9}{24}$
	$=$	$\frac{23}{24}$

Aufgaben zum Belegen von Termvariablen

Variablen belegen und Termwert berechnen

Teil 1: Variablen belegen

Teil 2: Termwert berechnen

Ergebnis:

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

für x=−2

für x=−1

für x=−0,5

für x=0,25

für x=34

für x=1

Lösung für T1

Lösung für T2

Lösung für T3

Lösung für T4

Lösung für T5

Tabelle

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

für $x = - 2$

für $x = - 1$

für $x = - 0,5$

für $x = 0,25$

für $x = \frac{3}{4}$

für $x = 1$

Lösung für $T_{1}$

Lösung für $T_{2}$

Lösung für $T_{3}$

Lösung für $T_{4}$

Lösung für $T_{5}$