Wahlteil - GTR - lernen mit Serlo!

Aufgabe 1C

Gegeben ist die in $ℝ$ definierte Funktion $f$ mit $f (x) = \frac{1}{27} x^{3} - \frac{4}{3} x$ .

Der Graph von $f$ besitzt zwei Extrempunkte. Einer davon hat die $x$ -Koordinate $\sqrt{12}$ .

Der Graph von $f$ hat den Wendepunkt $(0 | 0) .$

Begründen Sie, dass der Graph von $f$ symmetrisch bezüglich seines Wendepunktes ist.
Bestimmen Sie die Koordinaten der Schnittpunkte des Graphen von $f$ mit den Koordinatenachsen. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Punktsymmetrie
Begründung, dass $f$ symmetrisch bezüglich seines Wendepunktes ist
Der Funktionsterm von $f$ (ganzrational) enthält nur ungerade Exponenten, d.h. der Graph von f ist punktsymmetrisch zum Koordinatenursprung $(0 | 0)$ und damit auch zu seinem Wendepunkt.
Schnittpunkte des Graphen von $f$ mit den Koordinatenachsen
Schnittpunkt mit der x-Achse:
$f (x) = 0$
Der GTR-Rechner liefert die Lösungen $x = - 6$ , $x = 0$ und $x = 6$ .
Damit erhält man die Punkte $(- 6 | 0), (0 | 0)$ und $(6 | 0)$ .
Schnittpunkt mit der y-Achse:
Setze $x = 0$ in $f (x)$ ein $\Rightarrow (0 | 0)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Betrachte die Exponenten von $f$ und schließe auf die Symmetrieeigenschaft.
Für die Schnittpunkte mit den Koordinatenachsen:
x-Achse: setze $f (x) = 0$ ;
y-Achse: setze $x = 0$ in $f (x)$ ein.
Es gibt Punkte des Graphen von $f$ , in denen die Tangente an den Graphen von $f$ parallel zur Geraden durch die beiden Extrempunkte des Graphen von $f$ ist.
Bestimmen Sie die Koordinaten dieser Punkte. (6 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Steigung der Geraden
Bestimme die Steigung der Geraden durch die beiden Extrempunkte $E_{1} (- \sqrt{12} | f (- \sqrt{12}))$ und $E_{2} (\sqrt{12} | f (\sqrt{12}))$ .
Steigung der Geraden: $m = \frac{f (\sqrt{12}) - f (- \sqrt{12})}{\sqrt{12} - (- \sqrt{12})}$
wegen Punktsymmetrie $\Rightarrow m = \frac{2 \cdot f (\sqrt{12})}{2 \sqrt{12}} = \frac{f (\sqrt{12})}{\sqrt{12}}$
Mit $f (\sqrt{12}) \approx - 3,079$ $\Rightarrow m \approx \frac{- 3,079}{\sqrt{12}} \approx - 0,89$
Demnach muss $f^{'} (x) \approx - 0,89$ sein.
Koordinaten der Extrempunkte
Die Gleichung $f^{'} (x) \approx - 0,89$ hat die Lösungen $x \approx - 2$ oder $x \approx 2$ .
Berechne $f (2) \approx - 2,4$ .
Wegen der Punktsymmetrie ist dann $f (- 2) \approx 2,4$ und man erhält die Punkte $(- 2 | 2,4)$ und $(2 | - 2,4)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme die Steigung der Geraden durch die beiden Extrempunkte.
Die Steigung dieser Geraden muss gleich $f^{'} (x)$ sein.
Bestimmen Sie alle Werte für $d$ , sodass der Graph zu $f (x) + d$ genau zwei Nullstellen besitzt. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsgraphen verschieben
Werte für $d$ , sodass der Graph zu $f (x) + d$ genau zwei Nullstellen besitzt
Der Graph von $f$ muss parallel zur y-Achse verschoben werden, sodass aus einem Extrempunkt eine Nullstelle wird.
Dafür gibt es zwei Möglichkeiten:
$d_{1} = f (- \sqrt{12}) \approx 3,079$ und $d_{2} = f (\sqrt{12}) \approx - 3,079$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Graph von $f$ muss parallel zur y-Achse verschoben werden, sodass aus einem Extrempunkt eine Nullstelle wird.
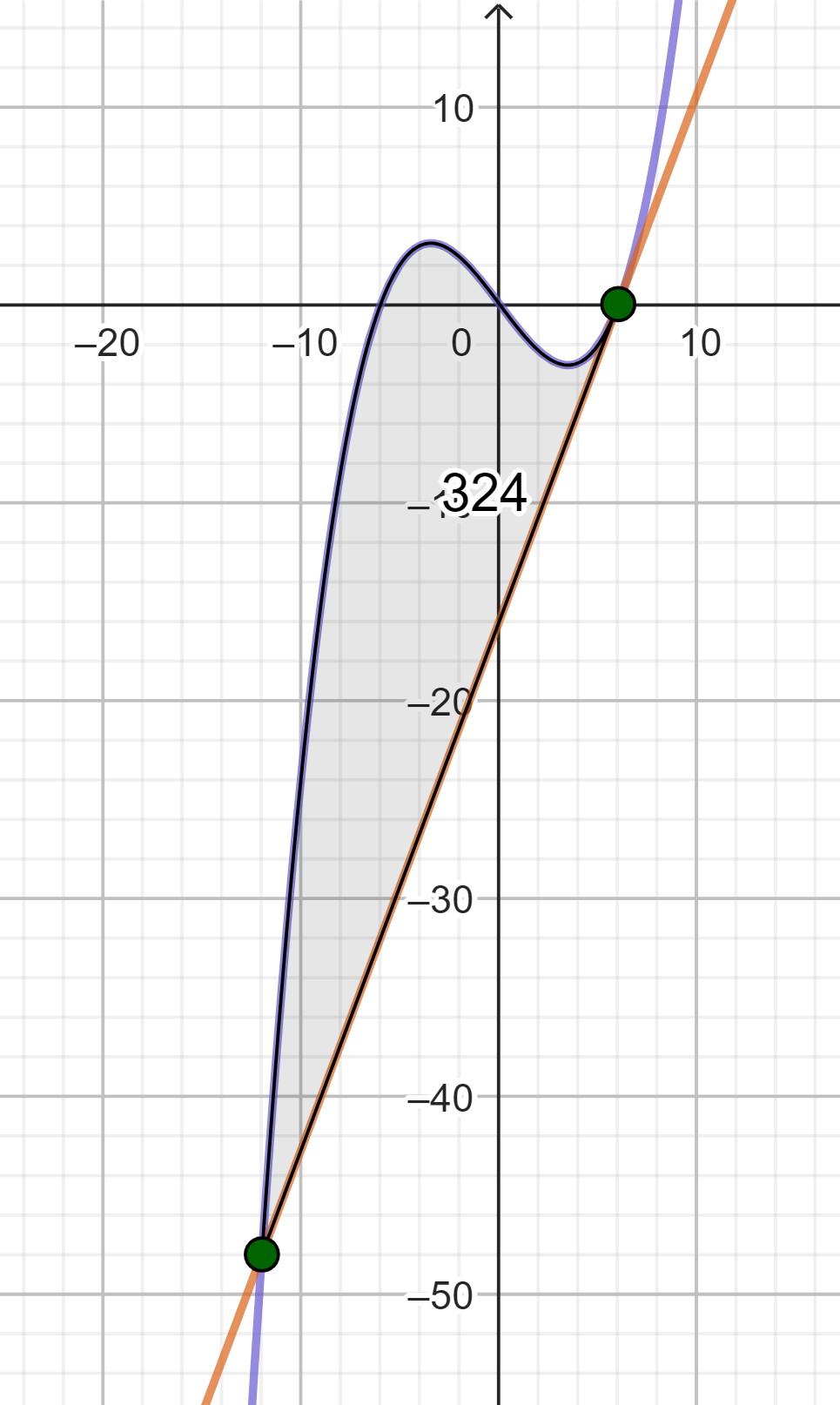
Die Tangente $t$ an den Graphen von $f$ im Punkt $P (6 | f (6))$ hat die Gleichung
$t (x) = \frac{8}{3} x - 16$ . Der Graph von $f$ und die Tangente $t$ schließen eine Fläche ein.
Bestimmen Sie den Inhalt dieser Fläche. (4 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Schnittpunkte zwischen den Graphen von $f$ und von $t$
Der GTR-Rechner liefert die Schnittpunkte $(6 | 0)$ und $(- 12 | - 48)$ .
Demnach gilt für die gesuchte Fläche:
$A = \int_{- 12}^{6} (f (x) - t (x)) d x = 324$
Die folgende Abbildung ist nicht gefordert. Sie dient nur zur Veranschaulichung.
Skizze
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme die x-Koordinaten der Schnittpunkte $x_{1}$ , $x_{2}$ zwischen den Graphen von $f$ und von $t$ .
Berechne dann das Integral $\int_{x_{1}}^{x_{2}} (f (x) - t (x)) d x$
Der Graph von $f$ soll in drei Schritten verändert werden. Die drei Schritte sind:
- Spiegeln an der $x$ -Achse
- Verschieben um 6 in positive $x$ -Richtung
- Verschieben um 14 in positive $y$ -Richtung
Geben Sie an, wie viele verschiedene neue Graphen entstehen, nachdem die drei Schritte in allen möglichen Reihenfolgen ausgeführt wurden.
Begründen Sie Ihre Angabe. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsgraphen verschieben
Hilfestellung
Überlege Dir an einem einfachen Beispiel z.B. $f (x) = x^{2}$ wie sich die insgesamt 6 verschieden Reihenfolgen auswirken.
Lösung
Geben Sie an, wie viele verschiedene neue Graphen entstehen, nachdem die drei Schritte in allen möglichen Reihenfolgen ausgeführt wurden
Bei drei Schritten ergeben sich insgesamt $6$ Möglichkeiten für die Reihenfolge der Schritte.
Dabei entstehen aber nur $2$ verschiedene neue Graphen. An welcher Position in der Reihenfolge der drei Schritte die Verschiebung in x-Richtung steht, hat keinen Einfluss auf die Veränderung des Graphens.
Ausschlaggebend ist die Reihenfolge der beiden anderen Schritte.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Untersuche, wie viele Reihenfolgen es gibt, diese drei Schritte zu kombinieren.
Skizziere grob, wie die Graphen aussehen, die durch diese Abbildungen verändert werden. Entscheide damit, wie viele der Graphen unterschiedlich sind.
Wird der Graph von $f$ den drei Schritten in der angegebenen Reihenfolge unterzogen, so entsteht der Graph der in $ℝ$ definierten Funktion $g$ mit
$g (x) = - \frac{1}{27} x \cdot (x - 6) \cdot (x - 12) + 14$ .
Die Abbildung zeigt den Graphen von $g$ .

Die Funktion $g$ beschreibt für $0 \leq x < 12$ den Verlauf der Tagesdurchschnittstemperatur an einem bestimmten Ort. Dabei ist $x$ die seit einem bestimmten Tag des Kalenderjahres vergangene Zeit in Monaten und $g (x)$ die Temperatur in $^{\circ} C$ .
Geben Sie die Bedeutung der Wendestelle von $g$ hinsichtlich des Verlaufs der Tagesdurchschnittstemperatur an. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
Bedeutung der Wendestelle von $g$ hinsichtlich des Verlaufs der Tagesdurchschnittstemperatur an
Der Wendepunkt ist der Punkt, an dem der Graph der Funktion die größte Steigung hat.
Die Wendestelle gibt demnach den Zeitpunkt mit dem größten Anstieg der
Tagesdurchschnittstemperatur an.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Der Wendepunkt ist der Punkt, an dem der Graph der Funktion die größte Steigung hat.
Welche Aussage über die Wendestelle ist dann möglich?
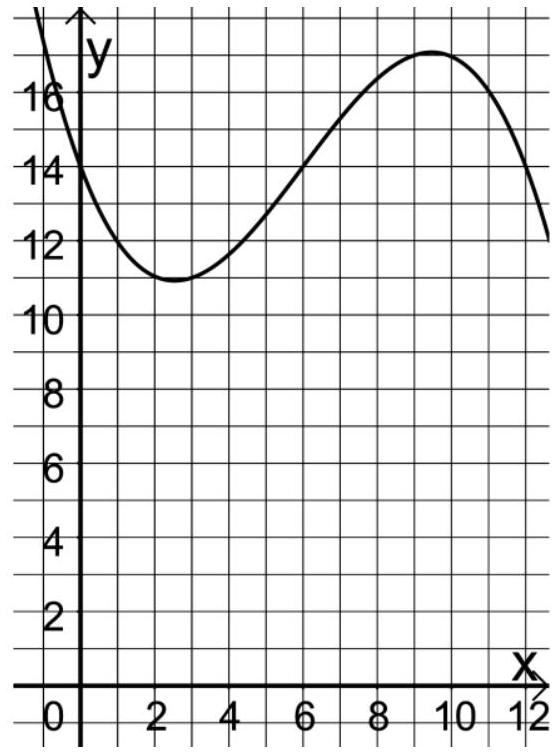
Die folgenden Rechnungen stellen in Verbindung mit der Abbildung die Lösung einer Aufgabe im Sachzusammenhang dar:

$g^{'} (x) = 0 \Leftrightarrow x = 6 - \sqrt{12}$ oder $x = 6 + \sqrt{12}$
$g (6 + \sqrt{12}) - g (6 - \sqrt{12}) \approx 6,2$
Geben Sie eine passende Aufgabenstellung an.
Erläutern Sie den dargestellten Lösungsweg. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Passende Aufgabenstellung
Berechnen Sie die Differenz zwischen der höchsten und der niedrigsten Tagesdurchschnittstemperatur.
Erläutern Sie den dargestellten Lösungsweg
In der ersten Zeile wird die 1. Ableitung von $g$ gleich null gesetzt, um mögliche Extremstellen zu finden.
Die beiden möglichen Extremstellen sind $x = 6 - \sqrt{12}$ oder $x = 6 + \sqrt{12}$ .
In der zweiten Zeile wird die Differenz der zugehörigen Funktionswerte berechnet.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Welche Aufgabenstellung passt zu den zwei Rechenzeilen?
Teil 2
Betrachte die erste Zeile und gib an, was dort berechnet wird. Betrachte dann die zweite Zeile und gib an, was dort berechnet wird.
Entscheiden Sie, ob die Funktion $g$ für $x \geq 12$ geeignet ist, den Verlauf der
Tagesdurchschnittstemperatur an dem betrachteten Ort für ein weiteres Jahr zu beschreiben.
Begründen Sie Ihre Entscheidung. (3 BE)
- Die Funktion $g$ ist geeignet.
- Die Funktion $g$ ist nicht geeignet.
Begründung
Die Funktion g ist für $x \geq 12$ nicht geeignet, den Verlauf der Tagesdurchschnittstemperatur an dem betrachteten Ort für ein weiteres Jahr zu beschreiben.
Begründungen:
Für $x$ gegen unendlich geht $f (x)$ gegen minus unendlich und das entspricht nicht der Realität.
Für einen realistischen Temperaturverlauf sollte die Funktion periodisch sein und das ist $g$ nicht.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Untersuche, wie sich die Funktion $g$ verhält, wenn $x$ sehr groß wird.

Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen → Was bedeutet das?

Aufgabe 1C

Begründung, dass f symmetrisch bezüglich seines Wendepunktes ist

Schnittpunkte des Graphen von f mit den Koordinatenachsen

Hast du eine Frage oder Feedback?

Steigung der Geraden

Koordinaten der Extrempunkte

Hast du eine Frage oder Feedback?

Werte für d, sodass der Graph zu f(x)+d genau zwei Nullstellen besitzt

Hast du eine Frage oder Feedback?

Schnittpunkte zwischen den Graphen von f und von t

Hast du eine Frage oder Feedback?

Lösung

Hast du eine Frage oder Feedback?

Bedeutung der Wendestelle von g hinsichtlich des Verlaufs der Tagesdurchschnittstemperatur an

Hast du eine Frage oder Feedback?

Passende Aufgabenstellung

Erläutern Sie den dargestellten Lösungsweg

Hast du eine Frage oder Feedback?

Begründung

Hast du eine Frage oder Feedback?

Begründung, dass $f$ symmetrisch bezüglich seines Wendepunktes ist

Schnittpunkte des Graphen von $f$ mit den Koordinatenachsen

Werte für $d$ , sodass der Graph zu $f (x) + d$ genau zwei Nullstellen besitzt

Schnittpunkte zwischen den Graphen von $f$ und von $t$

Bedeutung der Wendestelle von $g$ hinsichtlich des Verlaufs der Tagesdurchschnittstemperatur an