Pflichtteil

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

Aufgabe 1

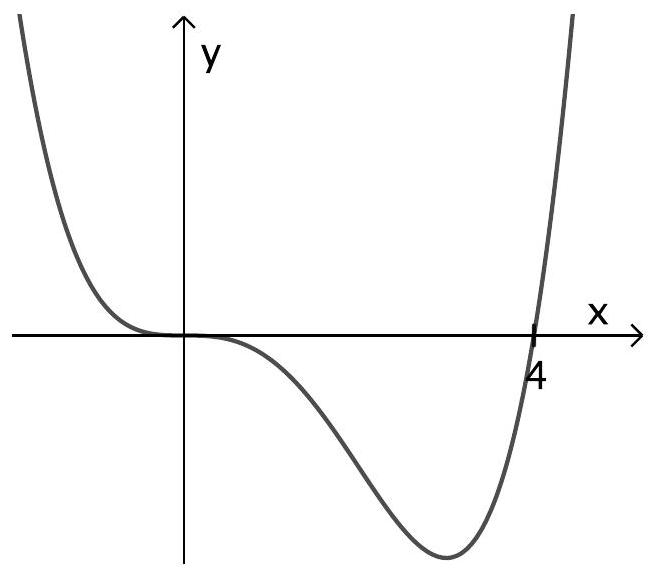
Gegeben ist die auf $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=2 e^{x}-4$ .

Berechnen Sie die Nullstelle von $f$ . (2 BE)

Bestimmen Sie eine Gleichung der Tangente an den Graphen von $f$ im Schnittpunkt mit der $y$ -Achse. (3 BE)

Aufgabe 2

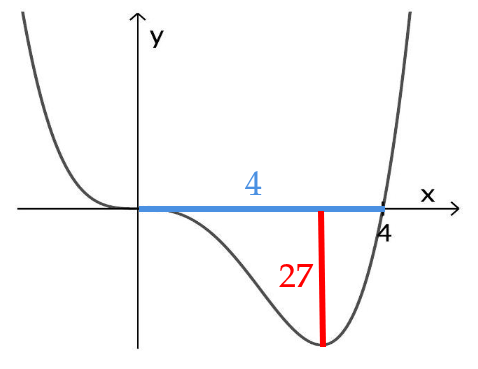
Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)=x^{4}-4 x^{3}$ .

Berechnen Sie den Wert des Integrals $\int_{0}^{1} f(x) d x$ . (2 BE)

Beurteilen Sie, ob die folgende Aussage richtig ist: (3 BE)
Für die Abbildung wurde eine Längeneinheit auf der $x$ -Achse ebenso groß gewählt wie auf der $y$ -Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Aussage beurteilen
Wir berechnen als Beispiel den Funktionswert $f(3)=3^4-4\cdot 3^3=81-108=-27$
Die Länge der roten Strecke sind $27$ Längeneinheiten. Verglichen mit der blauen Strecke kann nicht der gleiche Maßstab verwendet worden sein.
Die Aussage ist also falsch.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne einen Funktionswert zwischen $0< x < 4$ und begründe.

3
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 3
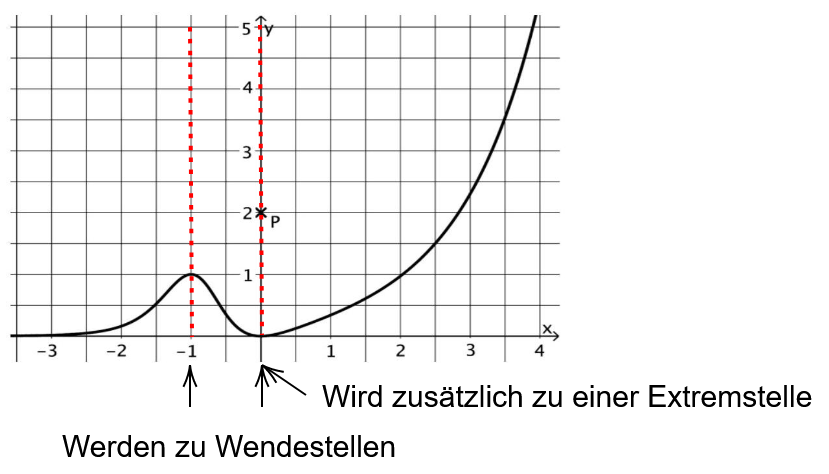
Die Abbildung zeigt den Punkt $P$ und den Graphen der in $\mathbb{R}$ definierten Funktion $f$ . Der Graph von $f$ hat die einzigen Extrempunkte $(-1 \mid 1)$ und $(0 \mid 0)$ .
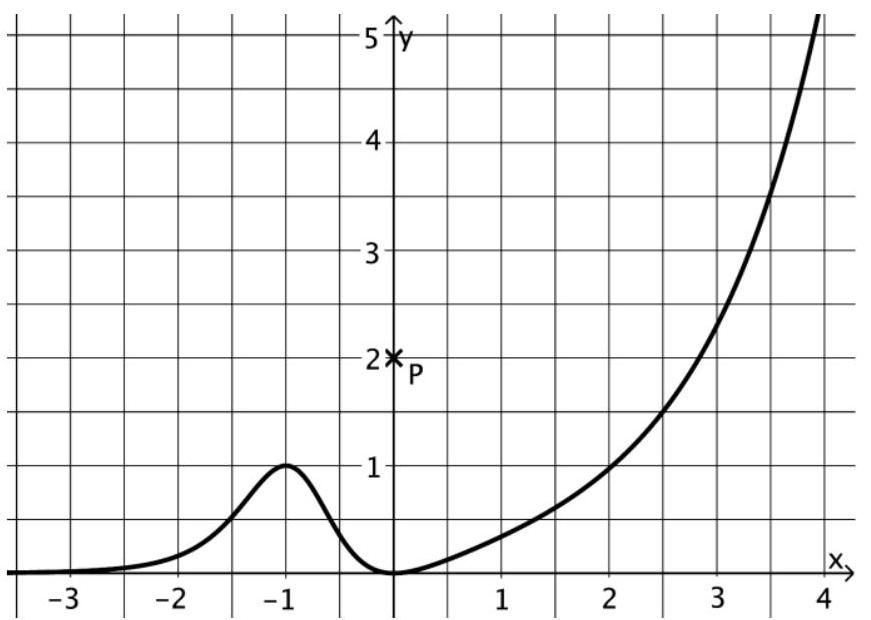
1. Gegeben ist die Funktion $g$ mit $g(x)=2 \cdot f(x-3)$ .
  Geben Sie die Koordinaten des Hochpunkts des Graphen von $g$ an. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verschieben in beliebige Richtung
  Koordinaten des Hochpunkts
  Der Graph wird um 3 Einheiten nach rechts verschoben:
  Anschließend wird der Graph in y-Richtung gestreckt. Jeder y-Wert wird mit 2 multipliziert.
  Der Hochpunkt des veränderten Graphen liegt bei $(2|2)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Koordinaten des Hochpunkts nach der Verschiebung in x-Richtung.
  Bestimme die Koordinaten des Hochpunkts nach der Streckung.
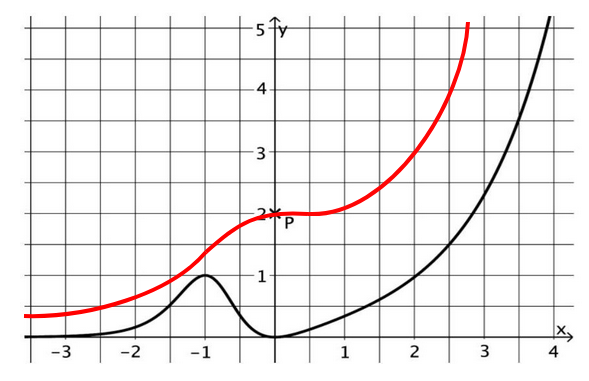
2. Der Graph einer Stammfunktion von $f$ verläuft durch den Punkt $P$ .
  Skizzieren Sie diesen Graphen in der Abbildung. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrale
  Stammfunktion skizzieren
  Beim grafischen Integrieren gilt umgekehrt wie beim grafischen Ableiten:
  Nullstellen werden zu Extremstellen der Stammfunktion
  Extremstellen werden zu Wendestellen der Stammfunktion
  Ein Wendepunkt, welcher gleichzeitig ein Extrempunkt ist, ist ein Sattelpunkt. Dieser liegt im Punkt $P$ :
  Möglicher Graph der Stammfunktion
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beim grafischen Integrieren gilt umgekehrt wie beim grafischen Ableiten:
  Nullstellen werden zu Extremstellen der Stammfunktion
  Extremstellen werden zu Wendestellen der Stammfunktion
  Zeichne den Graphen in y-Richtung so hoch ein, dass er durch den Punkt $P$ verläuft.

Aufgabe 4

Bei einem Spielautomaten gewinnt man in $30 \%$ aller Spiele.

Es werden $10$ Spiele gespielt. Die Anzahl der gewonnenen Spiele ist binomialverteilt.

Geben Sie einen Term an, mit dem die Wahrscheinlichkeit für das folgende Ereignis berechnet werden kann: (3 BE)

Es werden mindestens 2, aber weniger als 4 Spiele gewonnen.

Der Einsatz für ein Spiel beträgt $1 €$ . Gewinnt man ein Spiel, so werden $3 €$ ausgezahlt.
Berechnen Sie den auf lange Sicht zu erwartenden Gewinn pro Spiel. (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
Erwartungswert berechnen
Die möglichen Werte, die $Y$ annehmen kann sind $-1$ und $3$ (man verliert einen Euro oder gewinnt 2).
Die Wahrscheinlichkeit für einen Gewinn ist gegeben durch $p=0{,}3$ .
Übersicht
Y
P(Y)
$-1 ~€$
$0{,}7$
$3 ~€-1~€=2~€$
$0{,}3$
Der Erwartungswert beträgt:
$\displaystyle E[Y]$ $=$ $\displaystyle -1~€\cdot 0{,}7+2~€\cdot 0{,}3$
$=$ $\displaystyle -0{,}1~€$
Auf lange Sicht verliert man im Mittel pro Spiel $0{,}1~€$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Stelle die Gleichung für den Erwartungswert auf.
$Y$ bezeichnet jetzt die möglichen Beträge, die gewonnen/verloren werden können.

Y	P(Y)
$-1 ~€$	$0{,}7$
$3 ~€-1~€=2~€$	$0{,}3$

Aufgabe 5

Gegeben sind die Gerade $\def\arraystretch{1.25} g: \vec{x}=\left(\begin{array}{c}2 \\ 3 \\ -7\end{array}\right)+s \cdot\left(\begin{array}{l}1 \\ 0 \\ 5\end{array}\right)$ mit $s \in \mathbb{R}$ sowie die Gerade $h$ durch die Punkte $A(4|0| 0)$ und $B(6|0| b)$ mit einer reellen Zahl $b$ .

Begründen Sie, dass $A$ nicht auf $g$ liegt. (1 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie
Begründung
Wir schauen uns die Gerade genau an. Die zweite Zeile, die beschreibt, wie sich die Gerade in Richtung $x_2$ verhält, lautet:
Das heißt, für alle Werte für $s\in\mathbb{R}$ ist die $x_2$ -Koordinate $x_2=3$ .
Dann kann der Punkt $A(4|0| 0)$ nicht auf $g$ liegen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Untersuche die zweite Zeile der Geraden.
Begründe, dass die $x_2$ -Koordinate der Gerade nie $0$ sein kann.
Geben Sie eine Gleichung der Ebene an, die $g$ und $A$ enthält. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebenen
Vektoren aus der Gerade
Die Ebene hat in der Parameterform die Darstellung:
wobei $\overrightarrow{v},\overrightarrow{w}$ Richtungsvektoren sind und $\overrightarrow{a}$ der Stützvektor.
Wir übernehmen die Vektoren aus der Geraden:
Zweiter Richtungsvektor
Der zweite Richtungsvektor kommt aus der Verbindung von $A$ mit dem Stützvektor von $g$ :
Aufstellen der Ebene
Insgesamt ergibt sich für die Ebene:
für $t,s\in\mathbb{R}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Verwende die Parameterform, um die Ebene darzustellen.
Übernehme die Vektoren aus der Geraden und berechne den zweiten Richtungsvektor mithilfe des Punktes $A$ .

Bestimmen Sie den Wert für $b$ so, dass $g$ und $h$ parallel zueinander sind. (2 BE)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle 0$	$=$	$\displaystyle 2e^x-4$	$\displaystyle +4$
$\displaystyle 4$	$=$	$\displaystyle 2e^x$	$\displaystyle :2$
$\displaystyle 2$	$=$	$\displaystyle e^x$	$\displaystyle \ln\left(\right)$
	↓	Logarithmus anwenden, um Basis "wegzubekommen"
$\displaystyle \ln\left(2\right)$	$=$	$\displaystyle x$

$\displaystyle f(x)$	$=$	$\displaystyle 2e^x-4$
	↓	$e^x$ ist eigene Ableitung
$\displaystyle f'\left(x\right)$	$=$	$\displaystyle 2e^x$
$\displaystyle f'\left(0\right)$	$=$	$\displaystyle 2e^0$
	↓	$e^0=1$
	$=$	$\displaystyle 2$

$\displaystyle g\left(x\right)$	$=$	$\displaystyle f'\left(x_0\right)\left(x-x_0\right)+f\left(x_0\right)$
	$=$	$\displaystyle 2\cdot\left(x-0\right)-2$
	$=$	$\displaystyle 2x-2$

	$\displaystyle \int_0^1f(x)dx$
	↓ Stammfunktion verwenden
$=$	$\displaystyle \left[\frac{1}{5}x^5-x^4\right]_0^1$
	↓ Grenzen einsetzen
$=$	$\displaystyle \frac{1}{5}1^5-1^4-0$
$=$	$\displaystyle \frac{1}{5}-1$
$=$	$\displaystyle -\frac{4}{5}$

$\displaystyle P(X=k)$	$=$	$\displaystyle \binom{n}{k}p^k (1-p)^{n-k}$
	↓	$n=10$ Spiele $p=0{,}3$ für einen Gewinn $k=2,k=3$ gesucht
$\displaystyle P(2\le X\le 3)$	$=$	$\displaystyle P(X=2)+P(X=3)$
	↓	Einsetzen
	$=$	$\displaystyle \binom{10}{2}0{,}3^2 0{,}7^8+\binom{10}{3}0{,}3^3 0{,}7^7$

Pflichtteil

Aufgabe 1

Nullstelle berechnen

Hast du eine Frage oder Feedback?

Tangente an $f$ bestimmen

Hast du eine Frage oder Feedback?

Aufgabe 2

Stammfunktion bestimmen und Integral berechnen

Hast du eine Frage oder Feedback?

Aussage beurteilen

Hast du eine Frage oder Feedback?

Aufgabe 3

Koordinaten des Hochpunkts

Hast du eine Frage oder Feedback?

Stammfunktion skizzieren

Hast du eine Frage oder Feedback?

Aufgabe 4

Ereignis

Wahrscheinlichkeit

Hast du eine Frage oder Feedback?

Erwartungswert berechnen

Hast du eine Frage oder Feedback?

Aufgabe 5

Begründung

Hast du eine Frage oder Feedback?

Vektoren aus der Gerade

Zweiter Richtungsvektor

Aufstellen der Ebene

Hast du eine Frage oder Feedback?

Geradengleichung von $h$

Richtungsvektoren

Hast du eine Frage oder Feedback?

$\displaystyle E[Y]$	$=$	$\displaystyle -1~€\cdot 0{,}7+2~€\cdot 0{,}3$
	$=$	$\displaystyle -0{,}1~€$

$\displaystyle h:\ \vec{x}$	$=$	$\displaystyle \overrightarrow{OA}+t\cdot \overrightarrow{AB}\quad~\text{für }t\in\mathbb{R}$
	↓	Einsetzen
	$=$	$\def\arraystretch{1.25} \displaystyle \left(\begin{array}{c}4 \\ 0 \\ 0\end{array}\right)+t\cdot\left(\begin{array}{c}6-4 \\ 0-0 \\ b-0\end{array}\right)$
	$=$	$\def\arraystretch{1.25} \displaystyle \left(\begin{array}{c}4 \\ 0 \\ 0\end{array}\right)+t\cdot\left(\begin{array}{c}2 \\ 0 \\ b\end{array}\right)$

Pflichtteil

Aufgabe 1

Nullstelle berechnen

Hast du eine Frage oder Feedback?

Tangente an fff bestimmen

Hast du eine Frage oder Feedback?

Aufgabe 2

Stammfunktion bestimmen und Integral berechnen

Hast du eine Frage oder Feedback?

Aussage beurteilen

Hast du eine Frage oder Feedback?

Aufgabe 3

Koordinaten des Hochpunkts

Hast du eine Frage oder Feedback?

Stammfunktion skizzieren

Hast du eine Frage oder Feedback?

Aufgabe 4

Ereignis

Wahrscheinlichkeit

Hast du eine Frage oder Feedback?

Erwartungswert berechnen

Hast du eine Frage oder Feedback?

Aufgabe 5

Begründung

Hast du eine Frage oder Feedback?

Vektoren aus der Gerade

Zweiter Richtungsvektor

Aufstellen der Ebene

Hast du eine Frage oder Feedback?

Geradengleichung von hhh

Richtungsvektoren

Hast du eine Frage oder Feedback?

Tangente an $f$ bestimmen

Geradengleichung von $h$