Pflichtteil - Analysis & Analytische Geometrie / Lineare Algebra
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Aufgabe P1
Eine Funktion ist gegeben durch .
Geben Sie die Koordinaten des Scheitelpunktes an. (2BE)
Bestimmen Sie eine Gleichung der Tangente an den Graphen von im
Punkt . (3BE)
- 2
Aufgabe P2
Gegeben ist die in definierte Funktion mit .
Einer der folgenden Graphen I, II und III stellt dar.
Geben Sie die Graphen an, die dafür nicht infrage kommen, und begründen Sie Ihre Angabe. (2BE)

Berechnen Sie den Inhalt der Fläche, die der Graph von und die -Achse einschließen. (3BE)
- 3
Aufgabe P3
Gegeben ist die in definierte Funktion mit .
Bestimmen Sie . (3BE)
Der Graph der Funktion kann aus dem Graphen von durch Spiegeln an der -Achse und Verschieben um 3 in positive -Richtung erzeugt werden.
Geben Sie einen Funktionsterm von an. (2BE)
- 4
Aufgabe P4
Gegeben sind die Punkte und . Der Koordinatenursprung wird mit bezeichnet.
Bestimmen Sie denjenigen Wert von , für den und den Abstand haben. (3BE)
Ermitteln Sie denjenigen Wert von , für den das Dreieck im Punkt rechtwinklig ist. (2BE)
- 5
Aufgabe P5
Die Abbildung zeigt einen Quader sowie die Ortsvektoren der Eckpunkte und . Die Grundfläche ist quadratisch.
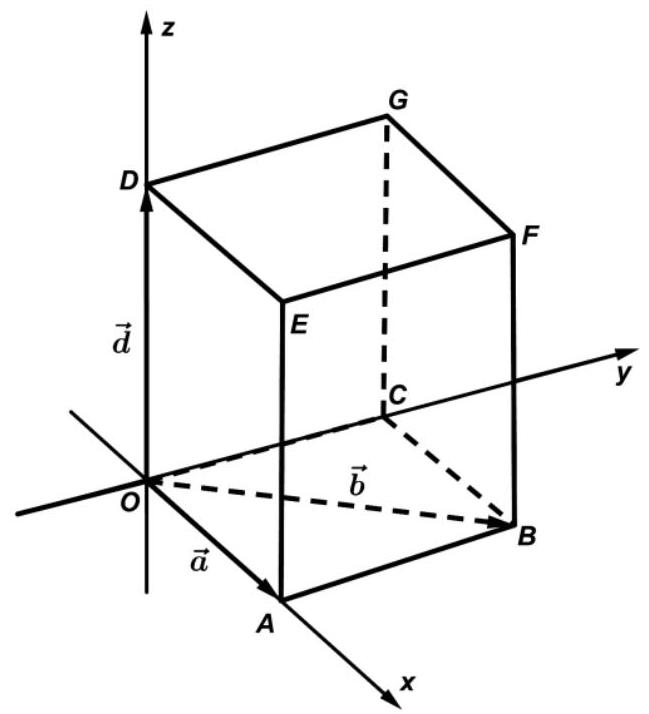
Beschreiben Sie die Lage des Punkts, zu dem der Ortsvektor gehört. (1BE)
Der Punkt hat den Ortsvektor .
Zeichnen Sie in die Abbildung ein. (1BE)
Begründen Sie, dass der Wert des Terms nur von der Seitenlänge der Grundfläche abhängt. (3BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?