Aufgaben zum Schnittwinkel von Geraden und Ebenen
Hier findest du Aufgaben zum Schnittwinkel zwischen Geraden und Ebenen. Lerne, mithilfe der Formel Winkel zu berechnen!
- 1
Bestimme den Schnittwinkel zwischen den beiden Geraden.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Berechne den Schnittwinkel zwischen den beiden Richtungsvektoren mit dem Skalarprodukt.
Setze die Richtungsvektoren der Geraden ein. Berechne das Skalarprodukt und die Beträge der Vektoren.
Verwende die Umkehrfunktion des Cosinus.
Dies ist augenscheinlich der größere der beiden Schnittwinkel. Der gesuchte (kleinere) Schnittwinkel ist also .
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Berechne den Schnittwinkel zwischen den beiden Richtungsvektoren mit dem Skalarprodukt.
Setze die Richtungsvektoren der Geraden ein. Berechne das Skalarprodukt und die Beträge der Vektoren.
Verwende die Umkehrfunktion des Cosinus
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Berechne den Schnittwinkel zwischen den beiden Richtungsvektoren mit dem Skalarprodukt.
Setze die Richtungsvektoren der Geraden ein. Berechne das Skalarprodukt und die Beträge der Vektoren.
Verwende die Umkehrfunktion des Cosinus.
Hast du eine Frage oder Feedback?
- 2
Bestimme den Schnittwinkel zwischen Gerade und Ebene.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel zwischen Gerade und Ebene berechnen
und
Bestimme den Schnittwinkel zwischen dem Normalenvektor
der Ebene und dem Richtungsvektor der Geraden mithilfe des
Skalarprodukts und des Betrags der Vektoren.
Verwende jetzt die Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
Berechne nun den gesuchten Schnittwinkel mit .
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel zwischen Gerade und Ebene berechnen
und
Bestimme zuerst den Normalenvektor der Ebene mit dem Kreuzprodukt:
Bestimme jetzt den Schnittwinkel zwischen dem Normalenvektor
der Ebene und dem Richtungsvektor der Geraden mithilfe des
Skalarprodukts und der Beträge der Vektoren.
Verwende die Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
Berechne nun den gesuchten Schnittwinkel mit .
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel zwischen Gerade und Ebene berechnen
und
Bestimme den Schnittwinkel zwischen dem Normalenvektor
der Ebene und dem Richtungsvektor der Geraden mithilfe des
Skalarprodukts und des Betrags der Vektoren.
Verwende die Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
Berechne nun den gesuchten Schnittwinkel mit .
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel zwischen Gerade und Ebene berechnen
und
Bestimme zuerst den Normalenvektor der Ebene mit dem Kreuzprodukt:
Bestimme den Schnittwinkel zwischen dem Normalenvektor
der Ebene und dem Richtungsvektor der Geraden mithilfe des
Skalarprodukts und des Betrags der Vektoren.
Verwende die Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
Berechne nun den gesuchten Schnittwinkel mit .
Der eingeschlossene Winkel beträgt also . Die Negativität des Ergebnisses oben folgt nur aus der speziellen Wahl der Richtungsvektoren.
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel zwischen Gerade und Ebene berechnen
und
Bestimme den Schnittwinkel zwischen dem Normalenvektor
der Ebene und dem Richtungsvektor der Geraden mithilfe des
Skalarprodukts und des Betrags der Vektoren.
Verwende die Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
Berechne nun den gesuchten Schnittwinkel mit .
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel zwischen Gerade und Ebene berechnen
und
Bestimme den Schnittwinkel zwischen dem Normalenvektor
der Ebene und dem Richtungsvektor der Geraden mithilfe des
Skalarprodukts und des Betrags der Vektoren.
Verwende die Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
Berechne nun den gesuchten Schnittwinkel mit .
Der eingeschlossene Winkel beträgt also . Die Negativität des Ergebnisses oben folgt nur aus der speziellen Wahl der Richtungsvektoren.
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel zwischen Gerade und Ebene berechnen
und
Bestimme den Schnittwinkel zwischen dem Normalenvektor
der Ebene und dem Richtungsvektor der Geraden mithilfe des
Skalarprodukts und des Betrags der Vektoren.
Verwende die Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
Berechne nun den gesuchten Schnittwinkel mit .
Hast du eine Frage oder Feedback?
- 3
Berechne den Schnittwinkel zwischen den beiden Ebenen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel berechnen
↓ Bestimme den Schnittwinkel zwischen den Normalenvektoren der Ebenen mit dem Skalarprodukt.
↓ Setze die beiden Vektoren ein.
↓ Berechne im Zähler das Skalarprodukt und im Nenner die Beträge der Vektoren.
↓ Bilde den Wert der Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
↓ Dies ist augenscheinlich der größere der beiden Schnittwinkel.
Der gesuchte Schnittwinkel ist also .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel berechnen
↓ Bestimme die Normalenvektoren der Ebenen mit dem Kreuzprodukt.
↓ Bestimme den Schnittwinkel zwischen den Normalenvektoren
der Ebenen mit dem Skalarprodukt .
↓ Setze die beiden Vektoren ein.
↓ Berechne im Zähler das Skalarprodukt und im Nenner die Beträge der Vektoren.
↓ Bilde den Wert der Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel berechnen
↓ Bestimme den Schnittwinkel zwischen den Normalenvektoren
der Ebenen mit dem Skalarprodukt .
↓ Setze die beiden Vektoren ein.
↓ Berechne im Zähler das Skalarprodukt und im Nenner die Beträge der Vektoren.
↓ Bilde den Wert der Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel berechnen
↓ Bestimme die Normalenvektoren der Ebenen mit dem Kreuzprodukt.
↓ Bestimme den Schnittwinkel zwischen den Normalenvektoren
der Ebenen mit dem Skalarprodukt .
↓ Setze die beiden Vektoren ein.
↓ Berechne im Zähler das Skalarprodukt und im Nenner die Beträge der Vektoren.
↓ Bilde den Wert der Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel berechnen
↓ Bestimme den Schnittwinkel zwischen den Normalenvektoren
der Ebenen mit dem Skalarprodukt .
↓ Setze die beiden Vektoren ein.
↓ Berechne im Zähler das Skalarprodukt und im Nenner die Beträge der Vektoren
↓ Bilde den Wert der Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
Hast du eine Frage oder Feedback?
↓ Bestimme den Schnittwinkel zwischen den Normalenvektoren
der Ebenen mit dem Skalarprodukt .
↓ Setze die beiden Vektoren ein.
↓ Berechne im Zähler das Skalarprodukt und im Nenner die Beträge der Vektoren.
↓ Bilde den Wert der Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
Hast du eine Frage oder Feedback?
↓ Bestimme die Normalenvektoren der Ebenen mit dem Kreuzprodukt.
↓ Bestimme den Schnittwinkel zwischen den Normalenvektoren
der Ebenen mit dem Skalarprodukt .
↓ Setze die beiden Vektoren ein.
↓ Berechne im Zähler das Skalarprodukt und im Nenner die Beträge der Vektoren.
↓ Bilde den Wert der Umkehrfunktion des Cosinus um den Winkel zu bestimmen.
↓ Dies ist augenscheinlich der größere der beiden Schnittwinkel. Der gesuchte Schnittwinkel ist also .
Hast du eine Frage oder Feedback?
- 4
Welchen Winkel schließen die Ebenen
und ein?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel in der analytischen Geometrie
Für die Berechnung des Schnittwinkels der beiden Ebenen gilt folgende Formel:
Du benötigst also von den Ebenen die Normalenvektoren und deren Beträge.
Die Ebene liegt in der Parameterform vor. Der Normalenvektor der Ebene muss also berechnet werden.
Dazu gibt es zwei Möglichkeiten:
Berechnung des Normalenvektors über das Vektorprodukt der beiden Richtungsvektoren.
Der Normalenvektor steht senkrecht auf den beiden Richtungsvektoren. Das Skalarprodukt zwischen dem Normalenvektor und jedem Richtungsvektor ist gleich null.
Möglichkeit 1
Möglichkeit 2
und
Wird jeweils das Skalarprodukt berechnet, so erhältst du zwei Gleichungen.
Aus Gleichung folgt
Bei zwei Gleichungen mit drei Unbekannten ist eine Variable frei wählbar.
Setze z.B. . Dann ist auch gleich .
Mit Gleichung folgt dann:
Damit ist .
Der Normalenvektor der Ebene kann abgelesen werden.
Berechne nun die Beträge der beiden Normalenvektoren.
Setze in die Formel für die Winkelberechnung ein:
Du hast die Gleichung erhalten.
Durch Anwendung der Umkehrfunktion des Kosinus kannst du den Winkel berechnen. Benutze auf dem Taschenrechner die Funktion .
Antwort: Der Schnittwinkel zwischen den beiden Ebenen beträgt .
Zusätzliche graphische Darstellung, die in der Aufgabenstellung nicht gefordert ist
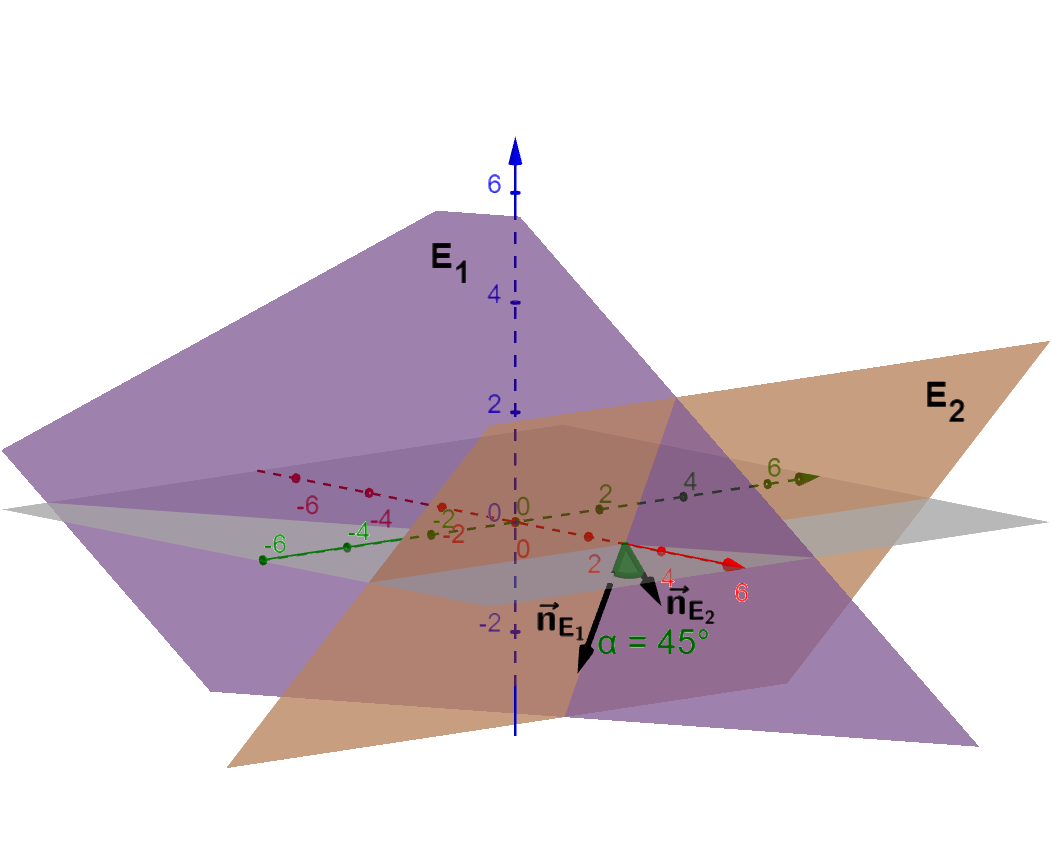
Berechne zuerst den Normalenvektor der Ebene . Verwende anschließend die Formel des Schnittwinkels zweier Vektoren (mit den Normalenvektoren der Ebenen).
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
