Teil B- Aufgabengruppe II

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

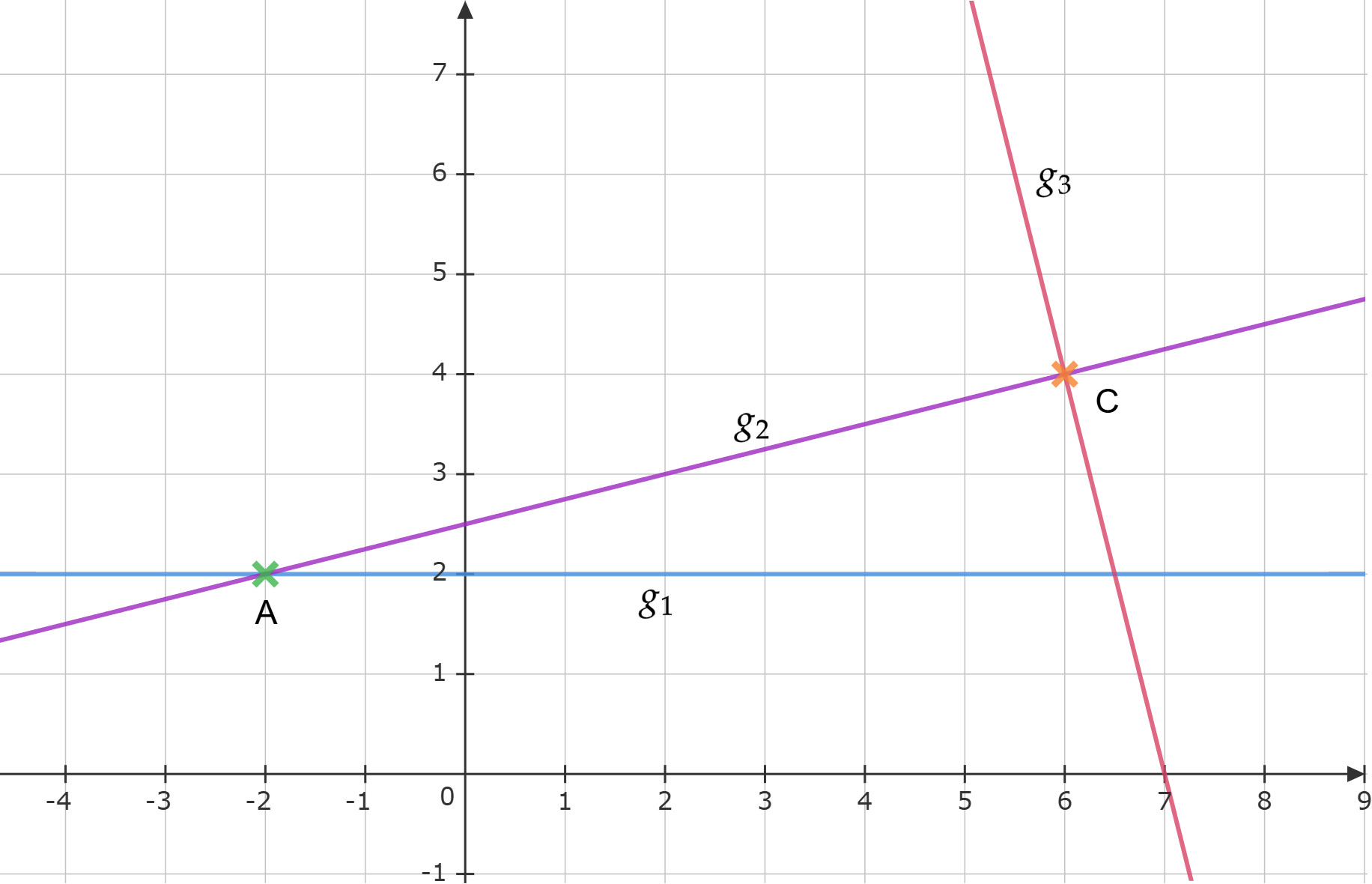
Gegeben sind die Geraden $\mathrm{g_1}$ , $\mathrm{g_2}$ und $\mathrm{g_3}$ sowie die Punkte $\mathrm{A (−2\ |\ 2)}$

und $\mathrm{C (6\ |\ 4)}$ .

Die Gerade $\mathrm{g_1}$ verläuft parallel zur $\text{x}$ -Achse und durch den Punkt $\text{A}$ .

Die Gerade $\mathrm{g_2}$ verläuft durch die Punkte $\text{A}$ und $\text{C}$ .

Die Gerade $\mathrm{g_3}$ schneidet $\mathrm{g_2}$ im Punkt $\text{C}$ und steht senkrecht auf $\mathrm{g_2}$ .

Zeichnen Sie die Geraden $\mathrm{g_1}$ , $\mathrm{g_2}$ und $\mathrm{g_3}$ in ein Koordinatensystem mit
der Längeneinheit $1\cm$ .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Markiere die Punkte $A$ und $C$
Zeichne die Geraden ein wie in der Aufgabenstellung beschrieben

Berechnen Sie den Abstand zwischen den Punkten $\text{A}$ und $\text{C}$ .

Geben Sie die Funktionsgleichung der Geraden $\mathrm{g_1}$ an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Die Steigung
Da die Funktion $g_{1}$ linear ist, ist ihr Graph eine Gerade. Diese verläuft parallel zur x-Achse und hat somit die Steigung $m = 0$ .
Der y-Achsenabschnitt
Die Gerade schneidet den Punkt $A (- 2 ∣ 2)$ , und da sie parallel zur x-Achse verläuft, liegt ihr y-Achsenabschnitt auch auf der Höhe $y = 2$ . Der y-Achsenabschnitt ist also $t = 2$ .
Die Funktionsgleichung
Mithilfe von der Steigung und dem y-Achsenabschnitt kann man jetzt die Funktionsgleichung aufstellen:
$y = m \cdot x + t \\ \Rightarrow y = 0 \cdot x + 2 \\ \Rightarrow y = 2$
Die Funktion hat also die Formel $g_1 (x) = 2 \,$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Bestimmen Sie rechnerisch die Funktionsgleichung der Geraden $\mathrm{g_2}$ .

Die Gerade $\mathrm{g_4}$ mit der Funktionsgleichung $\mathrm{g_4}$ : $\ \ \mathrm{\dfrac{1}{2}y + 1 − 3x = 0}\$ schneidet die

Gerade $\mathrm{g_5}$ : $\ \ \mathrm{y = − 0{,}5x + 4{,}5}$ im Punkt $\text{D}$ .

Ermitteln Sie rechnerisch die Koordinaten des Schnittpunkts $\text{D}.$

Geben Sie die Definitionsmenge der folgenden Gleichung an und ermitteln Sie

die Lösungsmenge rechnerisch.

\displaystyle {\dfrac{28x-12}{8}}\ =\ \dfrac{(x+3)^2}{x-1}

Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich bestimmen

Der Definitionsbereich

Um den Definitionsbereich zu bestimmen, muss man die Funktion auf Wurzeln, Logarithmen und Brüche testen.

Da in dieser Funktion weder Wurzeln noch Logarithmen auftreten, muss man nur darauf achten, dass in keinem Nenner eine $0$ steht.

Im Nenner auf der linken Seite steht eine $8$ , er kann also nie $0$ werden.

Im Nenner auf der rechten Seite steht ein $x$ , also setzt man den Term im rechten Nenner gleich $0$ :

$x - 1 = 0 \Rightarrow x = 1$

Setzt man in die Gleichung $1$ ein, so steht im Nenner eine $0$ . Also ist $1$ nicht Teil der Definitionsmenge.

$\Rightarrow \D = \R \, \setminus \{ 1 \}$

Die Lösungsmenge

Um die Lösungsmenge zu berechnen, stellt man die Gleichung zuerst so um, dass kein $x$ mehr im Nenner steht.

$\displaystyle \frac{28x - 12}{8}$	$=$	$\displaystyle \frac{\left( x + 3 \right) ^2}{x - 1}$	$\displaystyle \cdot \ 8 \cdot (x-1)$
$\displaystyle (28x - 12) \cdot (x-1)$	$=$	$\displaystyle (x + 3)^2 \cdot 8$
	↓	Klammern auflösen
$\displaystyle 28x^2 - 12x - 28x + 12$	$=$	$\displaystyle (x^2 + 6x + 9) \cdot 8$
$\displaystyle 28x^2 - 40x + 12$	$=$	$\displaystyle 8x^2 + 48x + 72$	$\displaystyle - 8x^2 - 48x - 72$
$\displaystyle 20x^2 - 88x - 60$	$=$	$\displaystyle 0$

Jetzt nutzt man die Mitternachtsformel, um nach $x$ aufzulösen:

$\displaystyle x_{1/2}$	$=$	$\displaystyle \frac{88 \pm \sqrt{(-88)^2 - 4 \cdot 20 \cdot (-60)}}{2 \cdot 20}$
$\displaystyle x_{1/2}$	$=$	$\displaystyle \frac{88 \pm \sqrt{7744 + 4800}}{40}$
$\displaystyle x_{1/2}$	$=$	$\displaystyle \frac{88 \pm \sqrt{12544}}{40}$
$\displaystyle x_{1/2}$	$=$	$\displaystyle \frac{88 \pm 112}{40}$

$x_1 = \dfrac{88 + 112}{40} = \dfrac{200}{40} = 5$

$x_2 = \dfrac{88 - 112}{40} = \dfrac{-24}{40} = -0{,}6$

$- 0,6$ und $5$ sind Lösungen der Gleichung.

$\Rightarrow \L = \{ -0{,}6; 5 \}$

Hinweis:

Die Rechnung wird übersichtlicher und einfacher, wenn man erkennt, dass man im Bruch ${\dfrac{28x-12}{8}}$ durch $4$ kürzen kann. Man löst also (mit demselben Vorgehen und natürlich derselben Lösung) die Aufgabe

\displaystyle {\dfrac{7x-3}{2}}\ =\ \dfrac{(x+3)^2}{x-1}

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Johannes kauft einen neuen Elektroroller im Wert von $3250\ €$ .

Ermitteln Sie rechnerisch, nach wie vielen Jahren dieser Elektroroller noch

einen Wert von $880\ €$ hätte, wenn man von einem jährlichen Wertverlust von

$23 %$ ausgeht.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechnen mit Logarithmus

Möglichkeit 1: Tabelle

Eine Möglichkeit, um die Lösung zu finden, ist, den Wert des Rollers für jedes neue Jahr zu berechnen, bis er $880 \ €$ erreicht.

Dafür multipliziert man den Wert des Rollers mit $100 \% - 23\% = 77\%$ , um $23 %$ vom abzuziehen.

vergangene Zeit in Jahren	1	2	3	4	5
Wert des Elektrorollers (gerundet)	$2502,5$	$1926,93$	$1483,73$	$1142,48$	$879,7$

Möglichkeit 2: Logarithmus

Die zweite Möglichkeit ist, eine Gleichung aufzustellen, bei der die Variable $x$ als die Anzahl der vergangenen Jahre definiert ist, und dann nach $x$ aufzulösen.

$\displaystyle 3250 \cdot 0{,}77^x$	$=$	$\displaystyle 880$	$\displaystyle : 3250$
$\displaystyle 0{,}77^x$	$=$	$\displaystyle \frac{880}{3250}$	$\displaystyle \log_{0{,}77}$
$\displaystyle x$	$=$	$\displaystyle \log_{0{,}77} \left( \frac{880}{3250} \right)$
$\displaystyle x$	$\approx ≈$	$\displaystyle 5$

Nach $5$ Jahren hat der Roller einen Wert von ca. $880 \ €$ erreicht.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Der Roller verliert in Wirklichkeit aber anfangs schneller an Wert.
So beträgt die Wertminderung im ersten Jahr $26 %$ , im zweiten Jahr $24 %$
und in den beiden Folgejahren jeweils $18{,}5\ \%$ .
Berechnen Sie den Wert des Elektrorollers nach diesen vier Jahren.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentrechnung mittels Formeln
Um den Wert des Rollers nach dem ersten Jahr zu berechnen, zieht man vom Anfangswert den Verlust ab.
Den Verlust berechnet man, indem man den Anfangswert mit der Wertminderung multipliziert.
$3250 - (3250 \cdot 0{,}26) = 3250 - 845 = 2405$
Dann rechnet man genauso für die folgenden drei Jahre:
$2405 - (2405 \cdot 0{,}24) = 2405 - 577{,}2 = 1827{,}8$
$1827{,}8 - (1827{,}8 \cdot 0{,}185) =1827{,}8 - 338{,}143 = 1489{,}657$
$1489{,}657 - (1489{,}657 \cdot 0{,}185) = 1489{,}657 - 275{,}586545 = 1214{,}070455$
Der Roller ist nach $4$ Jahren also ca. $1214{,}07 \, €$ Wert.
Alternative:
Der Roller hat nach dem ersten Jahr noch $74\%=0{,}74$ des ursprünglichen Werts von $3250\,€$ . Man kann den Restwert also berechnen, wenn man den Ausgangswert mit $0,74$ multipliziert. Genauso kann man den Wertverlust in den folgenden Jahren durch Multiplikationen mit $0,76$ und zweimal mit $0,815$ berechnen:
$\text{Restwert}=3250\cdot0{,}74\cdot0{,}76\cdot0{,}815\cdot0{,}815=1214{,}07$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Ein Schulfreund von Johannes kauft sich einen vier Jahre alten Elektroroller

im Wert von $1129\ €$ .

Berechnen Sie den Neupreis des Rollers bei einer jährlichen Wertminderung

von $21 %$ in den ersten vier Jahren.

Die nach oben geöffnete Normalparabel $p_{1}$ verläuft durch die Punkte
$\mathrm{A(−2|−3)}$ und $\mathrm{B(0|−3)}.$
Berechnen Sie die Funktionsgleichung von $\mathrm{p_1}$ in der Normalform.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktion
Berechnen der Funktionsgleichung von $\mathrm{p_1}$ in der Normalform.
Die allgemeine Form einer quadratischen Funktion lautet:
$\mathrm{f(x)=ax^2+bx+c}$
Da es sich um eine nach oben geöffnete Normalparabel handelt, ist der Öffnungsfaktor $\mathrm{a=1}.$
Wir bestimmen den Wert für $\textbf{c}$ , indem wir die Koordinaten des Punkts $\textbf{B}$ ind die allgemeine Form der quadratischen Gleichung einsetzen.
$\mathrm{1\cdot 0^2+b\cdot 0+c=-3}$
$\mathrm{0+c=-3\ \Rightarrow\ c=-3}$
Jetzt bestimmen wir den Wert für $\textbf{b}$ , indem wir die Koordinaten des Punkts $\textbf{A}$ in die allgemeine Form der quadratischen Gleichung einsetzen.
$\mathrm{(-2)^2+b\cdot (-2)-3=-3}$
$\mathrm{4-2b-3=-3\ \Rightarrow\ b=2}$
Die Normalform der Funktionsgleichung von $\mathrm{p_1}$ lautet:
$\boxed{\mathrm{p_1:\ y=x^2+2x-3}}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme den Öffnungsfaktor $\text{a}$
Bestimme $\text{c}$
Berechne $\text{b}$
Stelle die Funktionsgleichung von $\mathrm{p_1}$ , in der Normalform, auf.
Die nach unten geöffnete Normalparabel $\mathrm{p_2}$ hat den Scheitelpunkt $\mathrm{S_2 (2 | 1)}$ .
Ermitteln Sie rechnerisch die Funktionsgleichung von $\mathrm{p_2}$ in der Normalform.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktion
Rechnerische Ermittlung der Funktionsgleichung von $\mathrm{p_2}$ in der Normalform.
Die allgemeine Form einer quadratischen Funktion lautet:
$\mathrm{f(x)=ax+bx+c}$
Da es sich um eine nach unten geöffnete Normalparabel handelt, ist der Öffnungsfaktor $\mathrm{a=-1}.$
Der Scheitel der Parabel $\mathrm{p_{\tiny 2}}\$ ist laut Angabe: $\mathrm{S_2 (2 | 1)}$
Die Scheitelform lautet:
$\ \mathrm{f\left(x\right)=a(x-d)^2+e}$
Setzte die entsprechenden Werte in die Scheitelform ein.
$\mathrm{p_{\tiny 2}:y\ =\ -(x-2)^2+1}$
Wir bestimmen die Normalform der Funktionsgleichung, indem wir die Klammer auflösen und zusammenfassen.
$\mathrm{p_{\tiny 2}:y\ =\ -(x^2-4x+4)+1}$
Die Normalform der Funktionsgleichung von $\mathrm{p_2}$ lautet:
$\boxed{\mathrm{p_{\tiny 2}:y\ =\ -x^2+4x-3}}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme den Öffnungsfaktor $\text{a}$
Stelle die Scheitelform auf.
Stelle die Funktionsgleichung von $\mathrm{p_2}$ , in der Normalform, auf.
Zeichnen Sie die Parabeln $\mathrm{p_1}$ und $\mathrm{p_2}$ in ein Koordinatensystem mit der
Längeneinheit $1\cm$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Das zweidimensionale kartesische Koordinatensystem
Einzeichnen der Parabeln $\mathrm{p_1}$ und $\mathrm{p_2}$ in ein Koordinatensystem.
Die Skizze ist nicht maßtreu.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Die Parabel $p_{3}$ hat die Funktionsgleichung $p_{3}$ : $y = x^{2} - 14 x + 37$ .

Bestimmen Sie rechnerisch die Koordinaten des Scheitelpunkts $S_{3}$ .

Der Punkt $C (- 4 ∣ y)$ liegt auf der Parabel $p_{3}$ .

Berechnen Sie die y-Koordinate des Punkts $C$ .

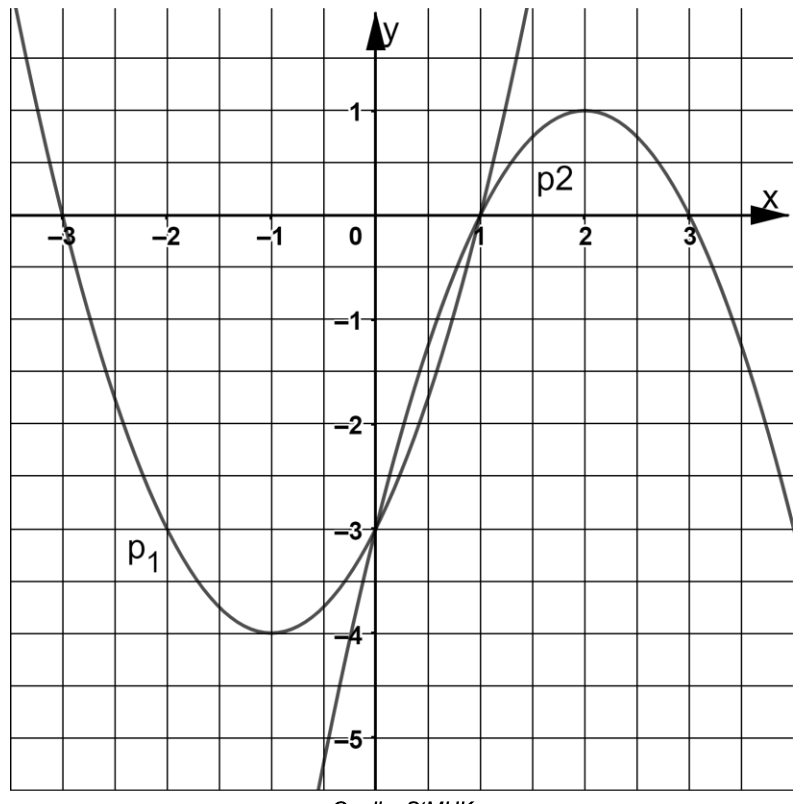
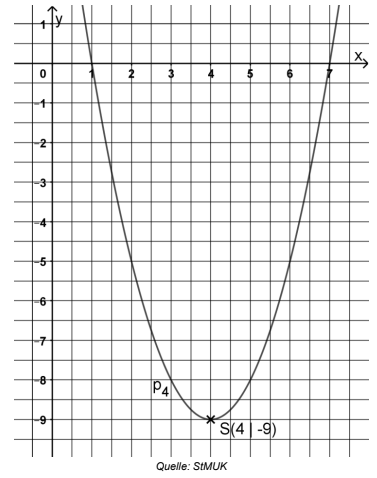
Die folgende Abbildung zeigt die Normalparabel $p_{4}$ .

Lesen Sie die x-Koordinaten der Nullstellen von $p_{4}$ aus dem Graphen ab

und überprüfen Sie diese rechnerisch.

In der folgenden Aufgabenstellung ist ein mathematischer Fehler enthalten.
„Gegeben ist die Parabel $p_{5}$ : y $= x^{2} - 6 x -$ 3. Berechnen Sie die Koordinaten
der zwei Schnittpunkte von $p_{5}$ mit der y-Achse.“
Ändern Sie die Aufgabenstellung so, dass sie mathematisch korrekt ist.
Notieren Sie diese auf Ihrem Lösungsblatt.
/8

Für diese Aufgabe benötigst Du folgendes Grundwissen: Was ist eine Funktion?
Geänderte Aufgabenstellung.
„Gegeben ist die Parabel $\mathrm{p_5: y = x^2 − 6x − 3}$ .
Berechnen Sie die Koordinaten des Schnittpunkts von $\mathrm{p_5}$ mit der $\text{y}$ -Achse.“
oder
„Gegeben ist die Parabel $\mathrm{p_5: y = x^2 − 6x − 3}$ .
Berechnen Sie die Koordinaten der zwei Schnittpunkte von $\mathrm{p_5}$ mit der $\text{x}$ -Achse.“
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

5
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
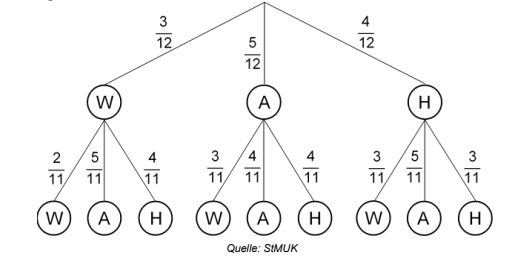
In einer Getränkekiste befinden sich ungeordnet $12$ Flaschen mit gleicher Form.
Drei Flaschen enthalten Wasser (W), fünf Flaschen Apfelschorle (A) und die
restlichen Holunderschorle (H).
Da die Kiste in einem sehr dunklen Kellerraum steht, sieht man erst nach dem
Verlassen des Raums, welches Getränk man entnommen hat.
Yannis holt sich zweimal nacheinander je eine Flasche aus der Kiste.
1. Stellen Sie die möglichen Ergebnisse in einem Baumdiagramm dar.
  Beschriften Sie die Äste mit den jeweiligen Wahrscheinlichkeiten.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
  Wasser (W): $3$ Flaschen
  Apfelschorle (A): $5$ Flaschen
  Holunderschorle (H): $4$ Flaschen
  Insgesamt: $12$ Flaschen
  Berechnung der Wahrscheinlichkeit bei der ersten Flaschenentnahme:
  Wahrscheinlichkeit (W): $\displaystyle\frac{3}{12}$
  Wahrscheinlichkeit (A): $\displaystyle\frac{5}{12}$
  Wahrscheinlichkeit (H): $\displaystyle\frac{4}{12}$
  Berechnung der Wahrscheinlichkeit bei der zweiten Flaschenentnahme und nunmehr $11$ Flaschen, analog.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die Wahrscheinlichkeit bei 12 Flaschen bei der ersten Flaschenentnahme.
  Berechne die Wahrscheinlichkeit bei 11 Flaschen bei der zewiten Flaschenentnahme in Abhängigkeit davon, welche Flasche bei der ersten Entnahme genommen wurde.
2. Berechnen Sie die Wahrscheinlichkeit, dass Yannis beide Male eine Flasche
  mit Holunderschorle entnimmt.
  
  Wahrscheinlichkeit, beide Male eine Holunderschorle zu entnehmen:
  $\displaystyle\frac{4}{12}\cdot\frac{3}{11}=\frac{1}{11}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Hier handelt es sich um ein mehrstufiges Zufallsexperiment.
  Multipliziere die Wahrscheinlichkeiten beim ersten und beim zweiten Mal ein Holunderschorle zu entnehmen.
3. Ermitteln Sie rechnerisch die Wahrscheinlichkeit dafür, dass keine der beiden
  Flaschen Apfelschorle enthält.
  
  Wahrscheinlichkeit beide Male keine Apfelschorle zu entnehmen (Gegenwahrscheinlichkeit):
  $\displaystyle 1-(\dfrac{5}{12}+\dfrac{3}{12}\cdot \dfrac{5}{11}+\dfrac{4}{12}\cdot \dfrac{5}{11})=1-(\frac{55}{11\cdot12}+\frac{15}{11\cdot12}+\frac{20}{11\cdot12})\\[1ex]=1-\frac{90}{11\cdot12}=1-\frac{15}{22}=\dfrac{7}{22}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  In diesem Fall musst du die Gegenwahrscheinlichkeit berechnen.
  Addiere die Wahrscheinlichkeiten beim ersten oder zweiten Mal ein Apfelschorle zu entnehmen.
  Subtrahiere die Summe von 1.
4. Geben Sie die Anzahl der möglichen Getränkekombinationen aus den zwei
  Flaschen an. Die Reihenfolge der Entnahme wird dabei nicht berücksichtigt.
  _/4
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kombinatorik
  Da genug Flaschen jeder Sorte vorhanden sind, wird die Anzahl der Möglichkeiten mit der Formel für "Ziehen mit Zurücklegen ohne Beachtung der Reihenfolge" berechnet.
  Es sind $n = 3$ Sorten, und es werden $k = 2$ Flaschen entnommen.
  Dann gibt es $\begin{pmatrix}n+k-1\\k \end{pmatrix}=\begin{pmatrix} 3+2-1\\2\end{pmatrix}=\begin{pmatrix}4\\2 \end{pmatrix}=6$ Möglichkeiten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Das wird mit Ziehen mit Zurücklegen ohne Reihenfolge berechnet.
6
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Bei folgender Figur gilt:
$|\overline{AE}| = 2{,}5 \cm$ ; $|\overline{AB}| = 9{,}5 \cm$ ; | $\overline{ED}| = 0{,}7 \cm$ ; $\delta=59°$
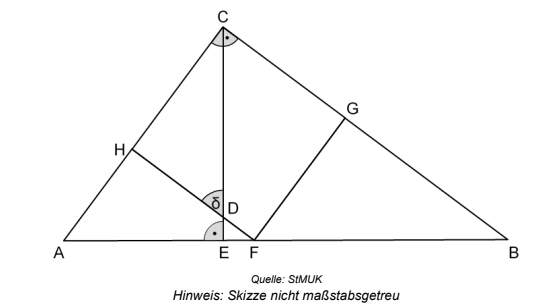
1. Berechnen Sie den Flächeninhalt des Quadrats CHFG.
  
  Für die Berechnung der Fläche des Quadrates CHFG benötigst du eine Seitenlänge, z.B. die Seitenlänge $\overline{CH}$ .
  Länge der Strecke $\overline{EB}$ in cm:
  | $\overline{EB}$ | $= 9,5 - 2,5$ => $|\overline{EB}|=7$
  Länge der Strecke $\overline{CE}$ in cm:
  Berechne $|\overline{CE}|$ mit Hilfe des Höhensatzes, Dreieck ABC.
  $|\overline{CE}|^2=2{,}5\cdot7$ => $|\overline{CE}|\approx4{,}18$
  Länge der Strecke $\overline{CD}$ in cm:
  $|\overline{CD}|=|\overline{CE}|$ − 0,7 => $|\overline{CD}|=3{,}48$
  Länge der Strecke $\overline{CH}$ in cm:
  Berechne $|\overline{CH}|$ mit Hilfe des Sinus, Dreieck DCH.
  $\displaystyle\sin(\alpha)=\frac{\text{Gegenkathete}}{\text{Hypotenuse}}$
  $\displaystyle\sin59°=\frac{|\overline{CH}|}{3{,}48}$
  $|\overline{CH}|=2{,}98$
  Flächeninhalt des Quadrates CHFG in $c m^{2}$ :
  $A_Q=2{,}98^2\approx8{,}88$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Um die Fläche des Quadrats CHFG zu berechnen , benötigst du eine Seitenlänge, z.B $|\overline{CH}|$ . Berechne diese wie folgt.
  Berechne die Länge der Strecke $|\overline{CE}|$ mit Hilfe des Höhensatzes, Dreieck ABC.
  Berechne die Länge der Strecke $|\overline{CD}|$ durch Subtraktion.
  Berechne die Länge der Strecke $|\overline{CH}|$ mit Hilfe des Sinus, Dreieck DCH .
  Berechne die Fläche des Quadrats.
2. Berechnen Sie die Länge der Kathete $\overline{AC}$ mithilfe des Kathetensatzes.
  /4
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Höhen- und Kathetensatz
  $|\overline{AC}|^2=\left|\overline{AE}|\cdot\right|\overline{AB}|$
  $|\overline{AC}|^2=2{,}5\cdot9{,}5$
  $|\overline{AC}|^{ }\approx4{,}87$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Bei einem massiven Werkstück ist auf die Grund- und Deckfläche eines Zylinders je eine Halbkugel aufgesetzt. Die Abbildung zeigt den Querschnitt des Werkstücks mit den entsprechenden Maßen.
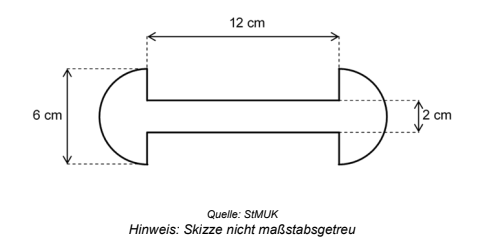
1. Das Werkstück besteht aus Aluminium. $1 \cm^3$ dieses Materials hat eine Masse von $2,7$ g.
  Berechnen Sie die Masse des Werkstücks.
  
  Volumen der Kugel in $c m^{3}$ :
  $V_K=\frac{4}{3}\cdot r^3 \cdot\pi$
  $r=3 \cm$
  $V_K=\frac{4}{3}\cdot\ 3^3 \cdot 3{,}14 = 113{,}04$
  Das Volumen der Kugel beträgt also $113{,}04\cm^3$ .
  Volumen des Zylinders in $c m^{3}$ :
  $V_\text{Zylinder}\boldsymbol= r^2\cdot π\cdot h$
  $r=1 \cm$
  $h=12 \cm$
  $V_\text{Zylinder}\boldsymbol= 1^2\cdot 3{,}14\cdot 12 = 37{,}68$
  Das Volumen des Zylinders beträgt $37{,}68\cm^3$ .
  Damit gilt für das Gesamtvolumen in $c m^{3}$ :
  $113,04 + 37,68 = 150,72$
  Masse in $g$ :
  $150{,}72\cdot2{,}7\approx406{,}94$
  Die Masse des Werkstücks entspricht somit $406{,}94 \,\mathrm{g}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne das Volumen der beiden Halbkugeln (sie bilden zusammen eine komplette Kugel).
  Berechne das Volumen des Zylinders.
  Addiere beide Volumina.
  Multipliziere das Gesamtvolumen mit der Masse pro $c m^{3}$ .
2. Die beiden Halbkugeln des Werkstücks erhalten einen farbigen Schutzanstrich. Die Mantelfläche des Zylinders wird nicht eingefärbt.
  Berechnen Sie den Oberflächeninhalt der zu färbenden Fläche.
  
  Oberflächeninhalt der Kugel in $c m^{2}$ :
  $O_{Kugel}=4\cdot r^2\cdot\pi$
  $O_{Kugel}=4\cdot3^2\cdot3{,}14 = 113{,}04$
  Somit ist der Oberflächeninhalt der Kugel durch $113{,}04\cm^2$ gegeben.
  Flächeninhalt Kreis:
  $A_{Kreis}=r^2\cdot\pi$
  Um den Flächeninhalt der zwei Kreisringe in $c m^{2}$ zu berechnen, kannst Du den Flächeninhalt des kleineren, inneren Kreises vom größeren, äußeren Kreis abziehen:
  $A_{Kreisring}=3^2 \cdot 3{,}14 -1^2 \cdot3{,}14 = 25{,}12$
  $A_{Zwei\ Kreisringe}=2\cdot 25{,}12 = 50{,}24$
  Der Flächeninhalt der beiden Kreisringe beträgt damit $50{,}24\cm^2$ .
  Gesamter Oberflächeninhalt in $c m^{2}$ :
  $113,04 + 50,24 = 163,28$
  Der Oberflächeninhalt der zu färbenden Fläche ist also $163{,}28\cm^2$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne die gesamte Oberfläche der beiden Kugelhälften.
  Berechne die Flächen der beiden Kreisringe außerhalb des Zylinders zwischen den beiden Kugelhälften.
  Addiere alle Flächen.
8
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
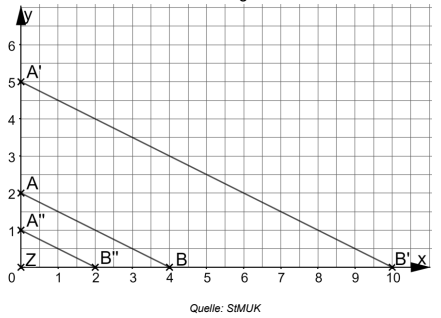
Gegeben sind die Punkte $A (0 ∣ 2)$ und $B (4 ∣ 0)$ sowie das Zentrum $Z (0 ∣ 0)$ .
Die Strecke $\overline{AB}$ wird durch eine zentrische Streckung mit dem Streckungsfaktor
$k_1=2{,}5$ auf die Strecke $\overline{A'B'}$ abgebildet.
Bei einer zweiten zentrischen Streckung wird die Strecke $\overline{AB}$ mit $k_2=0{,}5$
auf $\overline{A''B''}$ abgebildet.
Zeichnen Sie die Strecken $\overline{AB}$ , $\overline{A'B'}$ und $\overline{A''B''}$ in ein Koordinatensystem mit
der Längeneinheit $1 \cm$ und geben Sie den Streckungsfaktor $k_{3}$ für die Streckung
von $\overline{A'B'}$ auf $\overline{A''B''}$ an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zentrische Streckung (Konstruktion)
Streckungsfaktor:
$k_3=0{,}2$
9
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Bei einer Gleichung zur Anwendung einer binomischen Formel ist nur das gemischte Glied bekannt.
Stellen Sie eine mögliche vollständige Gleichung auf und notieren Sie diese auf Ihrem Lösungsblatt.
$\displaystyle (\square+\square)^2=\square+16x^8y^2+\square$
_/2

Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomische Formeln
Mögliche Lösung:
$(2x^8+4y^2)^2=4x^{16}+16x^8y^2+16y^4$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

	$\displaystyle d(A,B) $
$=$	$\displaystyle \sqrt{(x_C − x_A)^2 + (y_C − y_A)^2}$
$=$	$\displaystyle \sqrt{(6 − (-2))^2 + (4 − 2)^2}$
$=$	$\displaystyle \sqrt{8^2 + 2^2}$
$=$	$\displaystyle \sqrt{64 + 4}$
$=$	$\displaystyle \sqrt{68}$
$=$	$\displaystyle \sqrt{17 \cdot 4}$
$=$	$\displaystyle 2 \cdot \sqrt{17}$
$\approx ≈$	$\displaystyle 8{,}25$

$\displaystyle y$	$=$	$\displaystyle m \cdot x + t$
	↓	$A$ und $m$ einsetzen
$\displaystyle 2$	$=$	$\displaystyle \dfrac{1}{4} \cdot(-2) + t$
$\displaystyle 2$	$=$	$\displaystyle -0{,}5 + t$	$\displaystyle + \ 0{,}5$
$\displaystyle 2{,}5$	$=$	$\displaystyle t$

$\displaystyle \frac{1}{2} y + 1 - 3 x$	$=$	$\displaystyle 0$	$\displaystyle - 1 + 3 x$
$\displaystyle \frac{1}{2} y$	$=$	$\displaystyle 3x - 1$	$\displaystyle \cdot \ 2$
$\displaystyle y$	$=$	$\displaystyle 6x - 2$

$\displaystyle 6x - 2$	$=$	$\displaystyle -0{,}5x + 4{,}5$	$\displaystyle + 0{,}5x$
$\displaystyle 6{,}5x - 2$	$=$	$\displaystyle 4{,}5$	$\displaystyle +2$
$\displaystyle 6{,}5x$	$=$	$\displaystyle 6{,}5$	$\displaystyle : 6{,}5$
$\displaystyle x$	$=$	$\displaystyle 1$

$\displaystyle \text{y}$	$=$	$\displaystyle \mathrm{x^2-14x+37}$
	↓	quadratische Ergänzung
	$=$	$\displaystyle \mathrm{x^2-14x+\color{red}\left(\dfrac{14}{2}\right)^2\color{black}-\left(\dfrac{14}{2}\right)^2+37}$
	↓	in eine Binomische Formel umschreiben
	$=$	$\displaystyle \mathrm{\left(x-\color{red}7\color{black}\right)^2-\left(\dfrac{14}{2}\right)^2+37}$
	$=$	$\displaystyle \mathrm{\left(x-7\color{black}\right)^2-12}$

$\displaystyle x \cdot (0{,}79)^4$	$=$	$\displaystyle 1129$	$\displaystyle : (0{,}79)^4$
$\displaystyle x$	$=$	$\displaystyle \frac{1129}{0{,}79^4}$
$\displaystyle x$	$\approx ≈$	$\displaystyle 2898{,}58$

$\displaystyle \text{y}$	$=$	$\displaystyle x^2-14x+37$
	↓	einsetzen von $\text{x}=-4$
$\displaystyle \text{y}$	$=$	$\displaystyle (-4)^2-14\cdot(-4)+37$
	↓	ausmultiplizieren
$\displaystyle \text{y}$	$=$	$\displaystyle 16+56+37$
	↓	zusammenfassen
$\displaystyle \text{y}$	$=$	$\displaystyle 109$

$\displaystyle 0$	$=$	$\displaystyle (x-4)^2-9$	$\displaystyle -9$
	↓	subtrahieren
$\displaystyle 9$	$=$	$\displaystyle \mathrm{(x-4)^2}$	$\displaystyle \sqrt{}$
	↓	Wurzel ziehen
$\displaystyle \pm{3}$	$=$	$\displaystyle \mathrm{x-4}$	$\displaystyle +4$
	↓	addieren und Seiten tauschen
$\displaystyle \mathrm{x_{1}}$	$=$	$\displaystyle -3+4$
	↓	zusammenfassen
$\displaystyle \mathrm{x_1}$	$=$	$\displaystyle 1$
$\displaystyle \mathrm{x_2}$	$=$	$\displaystyle 3+4$
	↓	zusammenfassen
$\displaystyle \mathrm{x_2}$	$=$	$\displaystyle 7$

Teil B- Aufgabengruppe II

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Die Steigung

Der y-Achsenabschnitt

Die Funktionsgleichung

Hast du eine Frage oder Feedback?

Die Steigung

Der y-Achsenabschnitt

Die Funktionsgleichung

Hast du eine Frage oder Feedback?

Die x-Koordinate von DDD

Die y-Koordinate von DDD

Hast du eine Frage oder Feedback?

Der Definitionsbereich

Die Lösungsmenge

Möglichkeit 1: Tabelle

Möglichkeit 2: Logarithmus

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechnen der Funktionsgleichung von p1\mathrm{p_1}p1​ in der Normalform.

Hast du eine Frage oder Feedback?

Rechnerische Ermittlung der Funktionsgleichung von p2\mathrm{p_2}p2​ in der Normalform.

Hast du eine Frage oder Feedback?

Einzeichnen der Parabeln p1\mathrm{p_1}p1​ und p2\mathrm{p_2}p2​ in ein Koordinatensystem.

Hast du eine Frage oder Feedback?

Umformen der Normalform in die Scheitelform.

Hast du eine Frage oder Feedback?

Berechnen der y\text{y}y-Koordinate des Punkts C\text{C}C.

Hast du eine Frage oder Feedback?

Ablesen der Nullstellen von p4\mathrm{p_4}p4​ aus dem Graphen.

Rechnerische Überprüfung der Nullstellen.

Hast du eine Frage oder Feedback?

Geänderte Aufgabenstellung.

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Die x-Koordinate von $D$

Die y-Koordinate von $D$

Berechnen der Funktionsgleichung von $\mathrm{p_1}$ in der Normalform.

Rechnerische Ermittlung der Funktionsgleichung von $\mathrm{p_2}$ in der Normalform.

Einzeichnen der Parabeln $\mathrm{p_1}$ und $\mathrm{p_2}$ in ein Koordinatensystem.

Berechnen der $\text{y}$ -Koordinate des Punkts $\text{C}$ .

Ablesen der Nullstellen von $\mathrm{p_4}$ aus dem Graphen.