Betrachte die Funktion . Der Graph der Funktion ist und ihr Definitionsbereich .
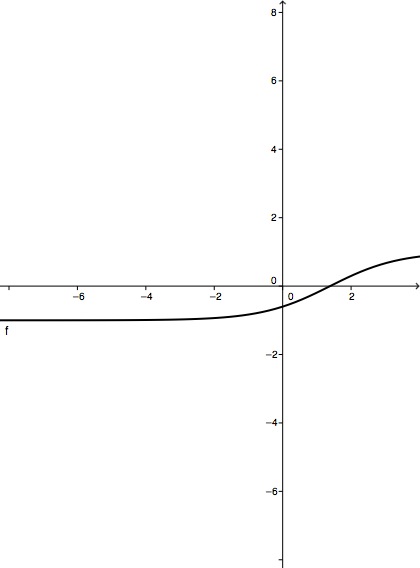
Berechne die Koordinaten des Schnittpunkts von mit der y-Achse.
Berechne anschließend die Koordinaten des Schnittpunkts von mit der x-Achse.
Bestimme das Verhalten von für und .
Untersuche das Monotonieverhalten von mit Hilfe der ersten Ableitung von .
ist der einzige Wendepunkt von . Zeige, dass die Gerade mit der Gleichung durch verläuft und auf der Wendetangente senkrecht steht.
Verschiebe um nach links, um den Graphen zu erhalten und gib an. Zeige, dass punktsymmetrisch zum Ursprung ist. Welche Bedeutung hat in diesem Fall der Punkt für ?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?


