Analysis, Teil A, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
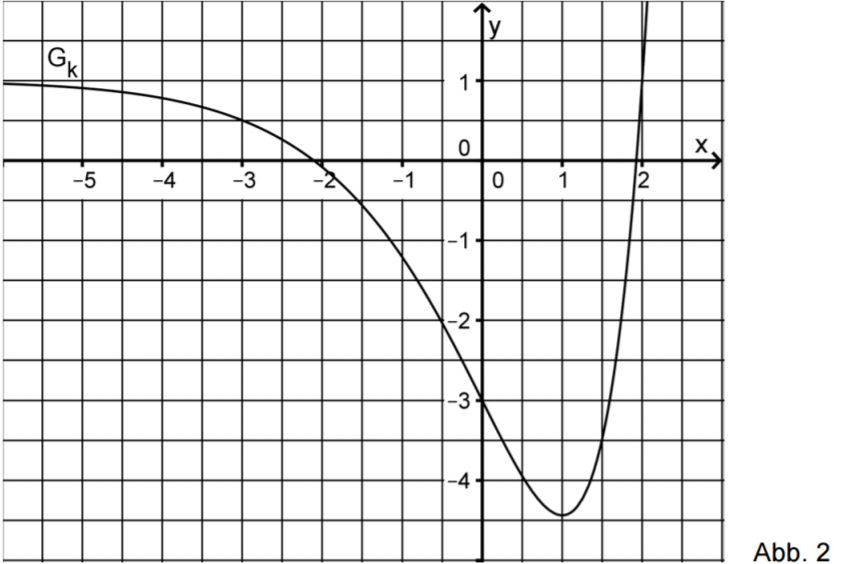
Abbildung $2$ zeigt den Graphen $G_k$ einer in $\mathbb{R}$ definierten Funktion $k$ .
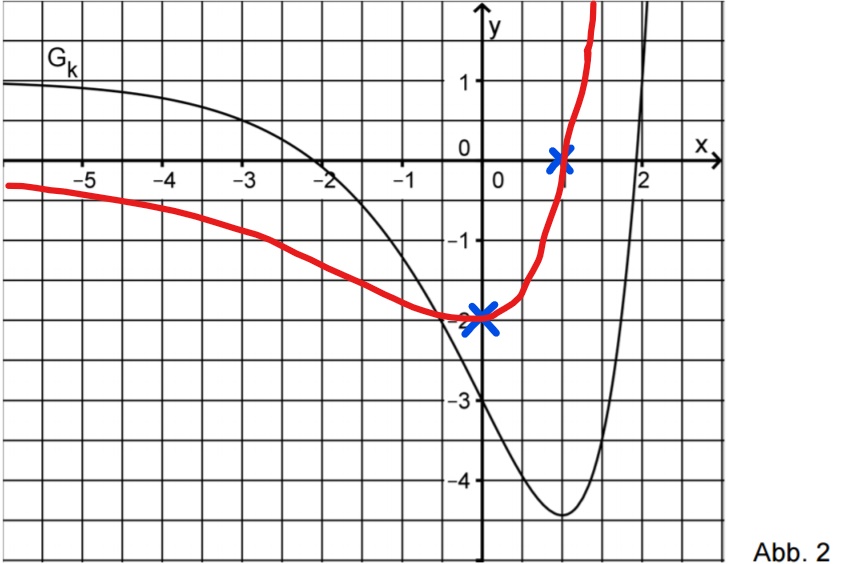
Skizzieren Sie in Abbildung $2$ den Graphen der zugehörigen Ableitungsfunktion $k'$ . Berücksichtigen Sie dabei insbesondere einen Näherungswert für die Steigung des Graphen $G_k$ an dessen Wendepunkt $(0|-3)$ sowie die Nullstelle von $k'$ . (4 BE)
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
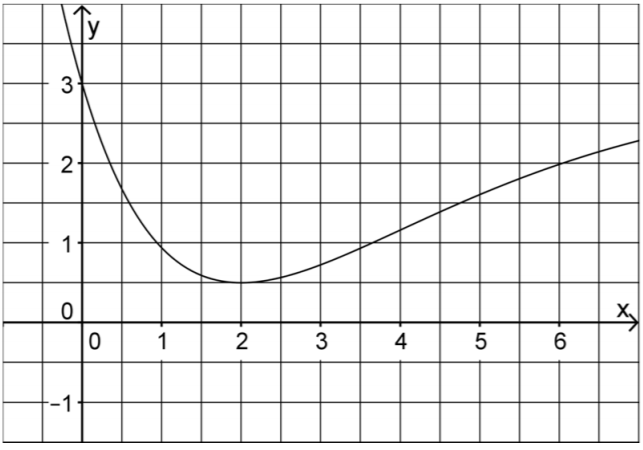
Abbildung 1 zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ .
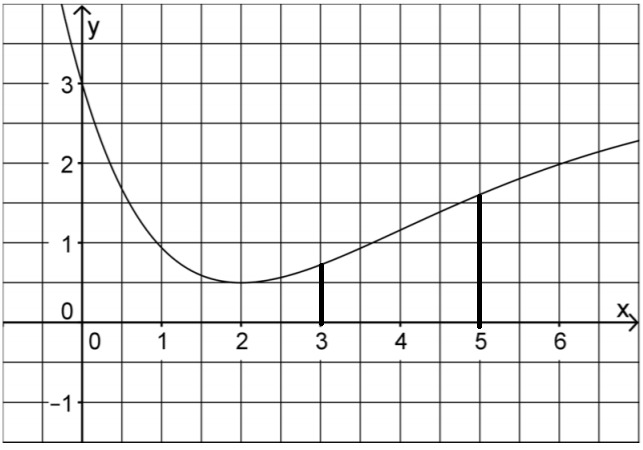
1. Bestimmen Sie mithilfe von Abbildung 1 einen Näherungswert für $\int_3^5{f(x)\text{d}}x$ . (2 BE)
  Die Funktion $F$ ist die in $\mathbb{R}$ definierte Stammfunktion von $f$ mit $F(3)=0$ .
2. Geben Sie mithilfe von Abbildung 1 einen Näherungswert für die Ableitung von $F$ an der Stelle $x=2$ an. (1 BE)
3. Zeigen Sie, dass $F(b)=\int_3^b{f(x)\text{d}}x$ mit $b \in \mathbb{R}$ gilt. (2 BE)
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Funktion $f:x \mapsto \frac{lnx}{x^2}$ mit maximalem Definitionsbereich $D$ .
1. Geben Sie $D$ sowie die Nullstelle von $f$ an und bestimmen Sie
  (3 BE)
2. Ermitteln Sie die $x$ -Koordinate des Punkts, in dem der Graph von $f$ eine waagrechte Tangente hat. (4 BE)
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Geben Sie jeweils den Term und den Definitionsbereich einer Funktion an, die die angegebene(n) Eigenschaft(en) besitzt.
1. Der Punkt $(2|0)$ ist ein Wendepunkt des Graphen von $g$ . (2 BE)
2. Der Graph der Funktion $h$ ist streng monoton fallend und rechtsgekrümmt. (2 BE)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?