Aufgaben zum Lösen linearer Gleichungssysteme

Löse die Linearen Gleichungssysteme mit dem Einsetzungsverfahren.

Gib die Lösungsmenge in der Form $(x;y)$ in das Eingabefeld ein. Beispiel: $(-2{,}5;1)$

Brüche werden mit einem "/" angegeben. Beispiel: $\frac38$ sind im Eingabefeld 3/8.

$\hphantom{\mathrm{I}}\mathrm{I} \quad 3x + 4 = y$

$\mathrm{II} \quad 4y -3x = 9$

$\hphantom{\mathrm{I}}\mathrm{I} \quad 3s - 4t = 4$
$\mathrm{II} \quad 4s + t = -2$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Einsetzungsverfahren
Als erstes musst du eine der beiden Gleichungen nach $s$ oder $t$ auflösen. Es bietet sich hier an, Gleichung $\mathrm{II}$ nach $t$ umzustellen.
Stelle Gleichung $\mathrm{II}$ nach $t$ um.
$\def\arraystretch{1.25} \begin{array}{crcll}\mathrm{II} & 4s + t &=& -2&|-4s\\&t&=&-2-4s\end{array}$
$\;$ Setze $t=-2-4s$ aus Gleichung $\mathrm{II}$ in $\mathrm{I}$ ein
$\hphantom{\mathrm{I}}\mathrm{I} \quad 3s - 4\cdot(-2 - 4s) = 4$
Multipliziere die Klammer aus und löse nach $s$ auf.
$\def\arraystretch{1.25} \begin{array}{crcll}\mathrm{I}&3s+8+16s&=&4&|-8\\&19s&=& -4&|:19\\&s&=&-\frac{4}{19}\end{array}$
Setze $s = -\frac{4}{19}$ in die umgeformte zweite Gleichung ein, um $t$ zu bestimmen.
$\def\arraystretch{1.25} \begin{array}{crcl}\mathrm{II} &t&=&-2-4\cdot(-\frac{4}{19})\\&t&=&-\frac{22}{19}\end{array}$
Gib nun noch die Lösungsmenge an.
$\mathbb{L}=\left\{(s|t)=\left(-\frac{4}{19}|-\frac{22}{19}\right)\right\}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

2
Löse die folgenden Gleichungssysteme mit 2 Gleichungen und 2 Variablen zunächst graphisch und dann rechnerisch.
Gib die Lösungsmenge in der Form $(x;y)$ in das Eingabefeld ein. Beispiel: $(-2{,}5;1)$
Brüche werden mit einem "/" in das Eingabefeld eingegeben. Beispiel: $\frac38$ wird zu 3/8.
1. $\def\arraystretch{1.25} \begin{array}{ccccc}\mathrm{I}&y& -& 3x& =& 1\\\mathrm{II}& x &+& y &=& 1\end{array}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichunssysteme
  Lineares Gleichungssystem mit zwei Unbekannten
  Ein lineares Gleichungssystem setzt sich aus mehreren linearen Gleichungen mit gemeinsamen Unbekannten (Variablen), die alle erfüllt werden sollen, zusammen.
  Graphisches Lösen
  Um das Gleichungssystem graphisch lösen zu können, kannst du die einzelnen Geichungen nach $y$ auflösen und in ein Koordinatensystem einzeichnen. Anschließend brauchst du nur noch die Koordinaten des Schnittpunktes beider Geraden abzulesen.
  $\def\arraystretch{1.25} \begin{array}{ccccc}\mathrm{I}&y -3x&=&1&|+3x\\\mathrm{I}&y& =& 3x+1\\\mathrm{II}& x + y &=& 1&|-x\\\mathrm{II}& y &=&-x+ 1\end{array}$
  Der Schnittpunkt liegt bei $x=0$ und $y=1$ . Somit lautet die Lösungsmenge $L=\left\{\left(0\left|\;1\right.\right)\right\}$ .
  Rechnerisches Lösen
  In diesem Fall bietet sich das Gleichsetzungsverfahren an, da du zum graphischen Lösen bereits beide Gleichungen nach $y$ aufgelöst hast.
  $\def\arraystretch{1.25} \begin{array}{ccccc}\mathrm{I}&y& =& 3x+1\\\mathrm{II}& y &=&-x+ 1\end{array}$
  Setze $\mathrm{I}$ und $\mathrm{II}$ gleich und löse nach $x$ auf.
  $\def\arraystretch{1.25} \begin{array}{rcccc}3x+1&=&-x+1&|-1\\3x&=&-x&|+x\\4x&=&0&|:4\\x&=&0\end{array}$
  Setze den erhaltenen Wert für $x$ in eine der Gleichungen ein, z.B in $\mathrm{II}$ .
  $y=0+1=1$
  Du kannst nun die Lösungsmenge angeben.
  $L=\left\{\left(0\left|1\right.\right)\right\}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $\def\arraystretch{1.25} \begin{array}{ccccc}\mathrm{I}&2y& +& 5x& =& 3\\\mathrm{II}& x &-& y &=& 1\end{array}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
  Lineares Gleichungssystem mit zwei Unbekannten
  Ein lineares Gleichungssystem setzt sich aus mehreren linearen Gleichungen mit gemeinsamen Unbekannten (Variablen), die alle erfüllt werden sollen, zusammen.
  Graphisches Lösen
  Um das Gleichungssystem graphisch lösen zu können, kannst du die einzelnen Geichungen nach $y$ auflösen und in ein Koordinatensystem einzeichnen. Anschließend brauchst du nur noch die Koordinaten des Schnittpunktes beider Geraden abzulesen.
  $\def\arraystretch{1.25} \begin{array}{ccccc}\mathrm{I}&2y+5x&=&3&|-5x\\\mathrm{I}&2y& =&-5x+3&|:2\\\mathrm{I}&y& =& -2{,}5x+1{,5}\\\mathrm{II}& x - y &=& 1&|-x\\\mathrm{II}& -y &=&-x+ 1&|\cdot(-1)\\\mathrm{II}& y &=&x- 1\end{array}$
  Der Schnittpunkt liegt bei $x\approx0{,}71$ und $y\approx-0{,}29$ . Somit lautet die Lösungsmenge $L=\left\{\left(0{,}71\left|\;-0{,}29\right.\right)\right\}$ .
  Rechnerisches Lösen
  In diesem Fall bietet sich das Gleichsetzungsverfahren an, da du zum graphischen Lösen bereits beide Gleichungen nach $y$ aufgelöst hast.
  $\def\arraystretch{1.25} \begin{array}{ccccc}\mathrm{I}&y& =& -2{,}5x+1{,5}\\\mathrm{II}& y &=&x- 1\end{array}$
  Setze $\mathrm{I}$ und $\mathrm{II}$ gleich und löse nach $x$ auf.
  $\def\arraystretch{2} \begin{array}{rcccc}-2{,}5x+1{,}5&=&x-1&|-x\\-3{,}5x+1{,5}&=&-1&|-1{,}5\\-3{,}5x&=&-2{,}5&|:(-3{,}5)\\x&=&\dfrac57\approx 0{,}71\end{array}$
  Setze den erhaltenen Wert für $x$ in eine der Gleichungen ein, z.B in $\mathrm{II}$ .
  $y=\dfrac57-1=-\dfrac27\approx-0{,}29$
  Du kannst nun die Lösungsmenge angeben.
  $L=\left\{\left(\dfrac57\left|-\dfrac27\right.\right)\right\}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $\def\arraystretch{1.25} \begin{array}{ccccc}\mathrm{I}&5y& -& 3x& =& 10\\\mathrm{II}& 4x &+& 5y &=& 16\end{array}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
  Lineares Gleichungssystem mit zwei Unbekannten
  Ein lineares Gleichungssystem setzt sich aus mehreren linearen Gleichungen mit gemeinsamen Unbekannten (Variablen), die alle erfüllt werden sollen, zusammen.
  Graphisches Lösen
  Um das Gleichungssystem graphisch lösen zu können, kannst du die einzelnen Geichungen nach $y$ auflösen und in ein Koordinatensystem einzeichnen. Anschließend brauchst du nur noch die Koordinaten des Schnittpunktes beider Geraden abzulesen.
  $\def\arraystretch{1.25} \begin{array}{ccccc}\mathrm{I}&5y-3x&=&10&|+3x\\\mathrm{I}&5y& =&3x+10&|:5\\\mathrm{I}&y& =& 0{,}6x+2\\\mathrm{II}& 4x+5y &=& 16&|-4x\\\mathrm{II}& 5y &=&-4x+ 16&|:5\\\mathrm{II}& y &=&-0{,}8x+3{,}2\end{array}$
  Der Schnittpunkt liegt bei $x\approx0{,}86$ und $y\approx2{,}51$ . Somit lautet die Lösungsmenge $L=\left\{\left(0{,}86\left|\;2{,}51\right.\right)\right\}$ .
  Rechnerisches Lösen
  In diesem Fall bietet sich das Gleichsetzungsverfahren an, da du zum graphischen Lösen bereits beide Gleichungen nach $y$ aufgelöst hast.
  $\def\arraystretch{1.25} \begin{array}{ccccc}\mathrm{I}&y& =& 0{,}6x+2\\\mathrm{II}& y &=&-0{,}8x+3{,}2\end{array}$
  Setze $\mathrm{I}$ und $\mathrm{II}$ gleich und löse nach $x$ auf.
  $\def\arraystretch{2} \begin{array}{rcccc}0{,}6x+2&=&-0{,}8x+3{,}2&|-2\\0{,}6x&=&-0{,}8x+1{,}2&|+0{,}8x\\1{,}4x&=&1{,}2&|:1{,}4\\x&=&\dfrac67\approx0{,}86\end{array}$
  Setze den erhaltenen Wert für $x$ in eine der Gleichungen ein, z.B in $\mathrm{I}$ .
  $y=0{,}6\cdot\dfrac67+2=\dfrac{88}{35}\approx2{,51}$
  Du kannst nun die Lösungsmenge angeben.
  $L=\left\{\left(\dfrac67\left|\dfrac{88}{35}\right.\right)\right\}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Auf einer Geburtstagsparty sind $30$ Kinder.
Du weißt, dass es viermal so viele Mädchen sind wie Jungen.
Wie viele Mädchen und Jungen sind es jeweils?
Löse mit einem Gleichungssystem!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichsetzungsverfahren
Tipp: Versuche die zwei Aussagen als Gleichungen aufzuschreiben und mithilfe eines Verfahrens für Gleichungssysteme zu lösen!
Gleichungen aus dem Text aufstellen
Wir wissen:
$30$ Kinder
$4$ Mal so viele Mädchen wie Jungen
Lege die Variablen fest.
$m$ : Anzahl der Mädchen
$j$ : Anzahl der Jungen
Es sind insgesamt $30$ Kinder! Jedes Kind ist entweder ein Mädchen oder ein Junge.
$\mathrm{I}\ \ m+j= 30$
Die Anzahl der Mädchen ist viermal die Anzahl der Jungen.
Zu beachten: Wir müssen die Anzahl der Jungen mit $4$ multiplizieren, nicht die der Mädchen!
$\mathrm{II} \ \ 4j=m$
Man hat jetzt ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten.
Bedenke, dass es drei mögliche Lösungsverfahren gibt.
In dieser Lösung wird das Einsetzungsverfahren verwendet.
Einsetzungsverfahren
1. Schritt: Löse nach einer Variablen auf
Sieh dir die zweite Gleichung an, diese ist schon nach $m$ aufgelöst.
2. Schritt: Setze $m$ in $\mathrm{I}$ ein
$m$ in $\mathrm{I}$
$\def\arraystretch{1.25} \begin{array}{rrl}4j + j &=& 30\\5j&=&30\\ j&=&\color{#009900}6 \end{array}$
3. Schritt: Setze $j$ in $\mathrm{II}$ ein
$j$ in $\mathrm{II}$
$\def\arraystretch{1.25} \begin{array}{rrl}4\cdot \color{#009900}6 &=&m\\\color{#cc0000}{24}&=&m\end{array}$
Lösungsmenge bestimmen
$\mathbb{L}=\{(j|m) = (6|24)\}$
Es sind also $6$ Jungs und $24$ Mädchen auf der Party.
4
Mick und Max gehen einkaufen. Mick kauft sich $3$ Schokoriegel und $2$ Eis und bezahlt $4{,}80\;$ €, Max kauft sich einen Schokoriegel und $2$ Eis für $3\;$ €. Kann sich Stefan ein Eis kaufen, wenn er $1{,}10\;$ € dabei hat?
Stefan kann sich ein Eis kaufen.
Stefan kann sich kein Eis kaufen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineares Gleichungssystem
Suche dir Variablen aus und stelle die Gleichungen auf
Stelle die Gleichungen möglichst gleich so auf, dass alle gleichen Variablen untereinander stehen.
$x\;\widehat{=}$ Schokoriegel, $y\;\widehat{=}$ Eis
$\def\arraystretch{1.25} \begin{array}{rrll}&\mathrm{I}& 3x + 2y &=& 4{,}80\\&\mathrm{II}& 1x + 2y &=& 3\end{array}$
Wie du siehst, kommt zwei mal $2y$ vor. Deswegen lässt sich hier das Additions-/Subtraktionsverfahren gut verwenden. Da hier dasselbe Vorzeichen in beiden Gleichungen vorliegt, musst du die Gleichungen subtrahieren.
Additions-/Subtraktionsverfahren
$\def\arraystretch{1.25} \begin{array}{llccll}&&\mathrm{I}& 3x &+& 2y &=& 4{,}80\\&- &\mathrm{II}& 1x &+& 2y &=& 3\\\hline&&&2x&+&0&=&1{,}80\end{array}$
Nach der ersten Variablen auflösen
$\def\arraystretch{1.25} \begin{array}{rrl}2x+0&=&1{,}80\;|:2\\x&=&\color{#009900}{0{,}90}\end{array}$
Setze $x$ in $\mathrm{I}$ oder $\mathrm{II}$ ein
$x$ in $\mathrm{II}$
$\def\arraystretch{1.25} \begin{array}{rrl}{\color{#009900}0{,}90} + 2y&=&3\\2y&=&2{,}10\\y&=&\color{#cc0000}{1{,}05}\end{array}$
Lösungsmenge
$\mathbb{L}=\{(x|y)=(0{,}9|1{,}05)\}$
Lösung im Sachkontext
Ein Schokoriegel kostet also $0{,}90\;$ € und ein Eis $1{,}05\;$ €. Stefan kann sich folglich ein Eis kaufen.
Erstelle aus dem Text ein lineares Gleichungssystem. Wähle eine Variable für die Schokoriegel und eine für das Eis.
5
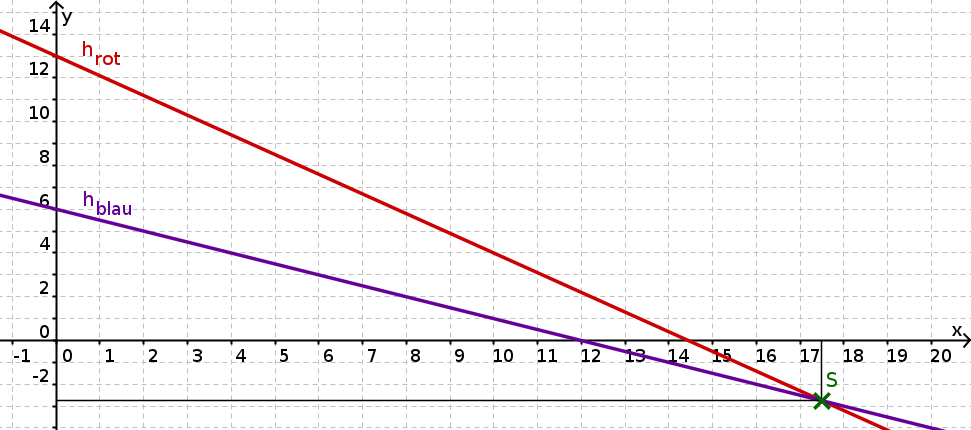
Brennende Kerzen
Beide Kerze brennen langsam herunter. Da die rote Kerze deutlich dünner ist als die blaue, wird sie schneller kleiner. Am Anfang der Beobachtung ist die blaue Kerze $6$ cm und die rote $13$ cm hoch. Man hat bereits beobachtet, dass in einer Stunde die blaue um $5$ mm und die rote $9$ mm gleichmäßig herunterbrennt.
1. Stelle für beide Kerzen jeweils eine Funktionsgleichung auf, die die Höhe $h$ in Abhängigkeit der Zeit $t$ darstellt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
  Blaue Kerze
  Man muss die Parameter der Gleichung $h_{blau}(t)=m_{blau}\cdot t+c_{blau}$ finden.
  In einer Stunde wird sie $0{,}5$ cm kleiner. Damit beträgt die Steigung $m_{blau} = -0{,}5$ .
  Der Y-Achsenabschnitt ist die anfängliche Höhe der Kerze: $c_{blau}=6$ .
  Du erhältst so die Funktionsgleichung: $h_{blau}(t)=-0{,}5\cdot t+6$
  Rote Kerze
  $h_{rot}(t)=m_{rot}\cdot t+c_{rot}$
  Pro Stunde verliert die rote Kerze $0{,}9$ cm. Die Steigung beträgt also $m_{rot} = -0{,}9$ .
  Die rote Kerze hat anfangs eine Höhe von $c_{rot}=13$ .
  Du erhältst so die Funktionsgleichung: $h_{rot}(t) = -0{,}9 \cdot t +13$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Höhe der Kerzen wird durch zwei lineare Funktionen beschrieben. Verwende als (abhängige) Variable $t$ statt $x$ , um zu verdeutlichen, dass die Höhe der Kerzen von der Zeit abhängt.
2. Berechne nun, nach wie vielen Stunden die Kerzen gleich lang sind, indem du die beiden Funktionen als Gleichungen mit den Variablen $h$ und $t$ auffasst.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichungssystem
  Zuerst stellst du aus den Funktionen ein Gleichungssystem mit zwei Variablen zusammen:
  $\def\arraystretch{1.25} \begin{array}{lrll}\hphantom{\mathrm{I}}\mathrm{I} &h &= &-0{,}5t+6 \\\mathrm{II} &h &= &-0{,}9t+13\end{array}$
  Um nun die Zeit $t$ zu finden, an der beide Kerzen die gleiche Höhe haben, suchst du die Lösung des Gleichungssystems. Dazu bietet sich das Gleichsetzungsverfahren gut an.
  Beide Gleichungen sind bereits nach $h$ aufgelöst und können direkt gleichgesetzt werden.
  1. Gleichsetzen
  $\Rightarrow -0{,}5t+6 = -0{,}9t+13$
  2. Nach t auflösen
  $\def\arraystretch{1.25} \begin{array}{rlll}-0{,}5t+6 &= &-0{,}9t+13 &|+0{,}9t\\0{,}4t + 6 &= &13 &|-6\\0{,}4t &= &7 &|:0{,}4\\t &= &17{,}5\end{array}$
  Die Kerzen sind also nach 17,5 Stunden, also 17 Stunden und 30 Minuten gleich hoch.
  Antwort: Nach 17 Stunden und 30 Minuten haben die Kerzen die gleiche Höhe $h$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Hinterfrage dein Ergebnis aus $b)$ kritisch im Kontext der Aufgabe. An welcher Stelle gibt es ein Problem?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichungssystem
  Höhe der Kerzen
  Nach Teilaufgabe b) haben die beiden Kerzen nach $17{,}5$ Stunden die gleiche Höhe. Doch wie groß sind sie? Wie bei allen Aufgaben zu Gleichungssystemen sollte man am Schluss die vollständige Lösungsmenge angeben: Das heißt zu der Zeit $t = 17{,}5$ muss noch die Höhe $h$ berechnet werden.
  Setze also $17{,}5$ in eine der Gleichungen aus b) ein und berechne $h$ .
  $\def\arraystretch{1.25} \begin{array}{lll}h &= &-0{,}5\cdot (\color{red}{17{,}5}) + 6 \\&= &-8{,}75 +6 \\&= &-2{,}75\end{array}$
  Setze dein Ergebnis beispielsweise in Gleichung $\mathrm{I}$ ein und vereinfache.
  Als Lösungsmenge ergibt sich also: Nach $17{,}5$ Stunden sind beide Kerzen $-2{,}75$ cm groß.
  Was bedeutet das $\color{red}{-}2{,}75$ cm?
  Mathematisch ergab sich für die beiden Geraden aus Teilaufgabe a) natürlich ein Schnittpunkt.
  Doch im Sachzusammenhang betrachtet, macht diese Lösung keinen Sinn. Aus der Geradengleichung der blauen Kerze $h_{blau} = -0{,}5t+6$ kann man berechnen, dass diese bereits nach $12$ Stunden abgebrannt ist. (siehe dazu Berechnung von Nullstellen)
  Alternativ kannst du dir auch die Graphen der Kerzen zeichnen, um deine Löusng zu interpretieren.
  Antwort:
  Obwohl sich rechnerisch eine Lösung ergibt, sind die beiden Kerzen niemals gleich groß: Sie sind vorher heruntergebrannt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne zuerst, auf welche Höhe die beiden Kerzen heruntergebrannt sind, wenn sie gleich groß sind. Versuche dann noch einmal deine Ergebnisse in Bezug auf zwei brennende Kerzen in Worte zu fassen.

Vater und Sohn sind zusammen 34 Jahre alt. Wie alt ist jeder von ihnen, wenn der Unterschied ihres Alters 26 Jahre beträgt?

Du hast dein Moped mit einer Mischung von Superbenzin und E10 getankt. Dabei hast du für $5$ Liter dieser Mischung insgesamt $6{,}50$ Euro bezahlt.

Wie viel Liter sind von jeder Sorte getankt worden, wenn $1$ Liter Superbenzin $1{,}35$ EUR und $1$ Liter E10 $1{,}20$ EUR kosten?

Stelle aus den gegebenen Informationen ein Gleichungssystem auf.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichungssysteme
Tipp: Bezeichne mit $x$ die getankten Liter von Superbenzin und mit $y$ die getankten Liter von E10.
Zunächst bezeichne die Größen mit geeigneten Variablen:
getankte Liter von Superbenzin $\widehat{=}$ $x$
getankte Liter von E10 $\widehat{=}$ $y$
Als nächstes musst du alle Informationen ordnen. Einerseits hast du Literangaben und andererseits hast du Geldangaben.
Wichtig: $x$ und $y$ sind in beiden Angaben enthalten.
Also:
Literangaben: $x$ Liter, $y$ Liter, $5$ Liter
Geldangaben: $1{,}35\cdot x$ Euro, $1{,}20\cdot y$ Euro, $6{,}50$ Euro
Im letzten Schritt stellst du aus den jeweiligen Angaben eine Gleichung auf.
Die erste Gleichung erhältst du durch die Information, dass $x$ Liter und $y$ Liter sich zu $5$ Liter addieren.
Die zweite Gleichung erhältst du durch die Information, dass $1{,}35\cdot x$ Euro und $1{,}20\cdot y$ Euro sich zu $6{,}50$ Euro addieren.
Sowohl Gleichung $\mathrm{I}$ als auch Gleichung $\mathrm{II}$ müssen laut Text erfüllt sein. Das Problem aus der Aufgabe kannst du also mit folgendem Gleichungssystem darstellen.
$\def\arraystretch{1.25} \begin{array}{rrll}\mathrm{I} &x& + &y& = 5\\\mathrm{II} &1{,}35\cdot x& + &1{,}2\cdot y& = 6{,}5\end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Löse das Gleichungssystem mit dem Gleichsetzungsverfahren. Beachte bei der Rechnung nicht den Sachzusammenhang.

Wie ist die gefundene Lösung aus Teilaufgabe b) im Sinne der ursprünglichen Aufgabe zu verstehen?

Es wurden $x = \frac{10}{3} \approx 3{,}3$ Liter Superbenzin und $y = \frac{5}{3} \approx 1{,}7$ Liter E10 getankt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

8
Dein Freund kauft bei einer großen Fastfood-Kette eine wilde Mischung aus Hamburger und Cheeseburger. Die Anzahl aller Burger beträgt $12$ und kosten zusammen $12{,}68$ Euro.
Es gilt: Ein Hamburger kostet $0{,}99$ Euro und ein Cheeseburger $1{,}19$ Euro.
1. Stelle mit den Informationen aus dem Text ein lineares Gleichungssystem auf.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineares Gleichungssystem
  Tipp: Bezeichne mit $x$ die Anzahl der Hamburger und mit $y$ die Anzahl der Cheeseburger.
  Zunächst bezeichne die Größen mit geeigneten Variablen:
  Anzahl der Hamburger $\widehat{=}$ $x$
  Anzahl der Cheeseburger $\widehat{=}$ $y$
  Als nächstes musst du alle Informationen ordnen. Einerseits hast du Mengenangaben und andererseits hast du Geldangaben.
  Wichtig: $x$ und $y$ sind in beiden Angaben enthalten.
  Also:
  Mengenangaben: $x$ Hamburger, $y$ Cheeseburger, Gesamtanzahl: $12$ Burger
  Geldangaben: $0{,}99\cdot x$ Euro, $1{,}19\cdot y$ Euro, $12{,}68$ Euro
  Im letzten Schritt stellst du aus den jeweiligen Angaben eine Gleichung auf.
  Die erste Gleichung erhältst du durch die Information, dass $x$ Hamburger und $y$ Cheeseburger sich zu $12$ Burger addieren.
  Die zweite Gleichung erhältst du durch die Information, dass $0{,}99\cdot x$ Euro und $1{,}19\cdot y$ Euro sich zu $12{,}68$ Euro addieren.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Zeige, dass $x = 8$ Hamburger und $y = 4$ Cheeseburger eine Lösung des Gleichungssystems ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineares Gleichungssystem
  Tipp: Du musst hier nicht das lineare Gleichungssystem ausrechnen. Es geht viel einfacher!
  Wenn du zeigen möchtest, dass $x$ und $y$ eine Lösung eines beliebigen linearen Gleichungssystems ist, musst du die Unbekannten in die Gleichungen des Systems einsetzen. Am Ende muss jede Gleichung eine wahre Aussage ergeben.
  Setze also $x = 8$ und $y = 4$ in die Gleichungen ein:
  $\def\arraystretch{1.25} \begin{array}{rrll}\mathrm{I} &x + y &= &12 \\\mathrm{II} &0{,}99\cdot x + 1{,}19\cdot y &= &12{,}68\end{array}$
  Setze die Werte ein.
  $\def\arraystretch{1.25} \begin{array}{rrll}\mathrm{I} &\color{#CC0000}{8} + \color{#009999}{4} &= &12 \\\mathrm{II} &0{,}99\cdot \color{#CC0000}{8} + 1{,}19\cdot \color{#009999}{4} &= &12{,}68\end{array}$
  Rechne aus. Falls links und rechts die gleiche Zahl steht, ist die Aussage wahr.
  $\def\arraystretch{1.25} \begin{array}{rrll}\mathrm{I} &\color{#FF6600}{12} &= &12 \\\mathrm{II} &\color{#FF6600}{12{,}68} &= &12{,}68\end{array}$
  Du siehst sofort, dass $x = 8$ Hamburger und $y = 4$ Cheeseburger eine wahre Aussage liefern.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Warum gibt es nur genau eine Lösung?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineares Gleichungssystem
  Ein lineares Gleichungssystem kann entweder keine, genau eine oder unendlich viele Lösungen haben.
  Die Gleichungen sind linear und nicht identisch. Zudem gibt es nur $2$ Gleichungen. Damit gibt es maximal nur einen Schnittpunkt. Maximal ein Schnittpunkt bedeutet, dass es entweder keinen oder einen Schnittpunkt gibt. Aus Aufgabenteil b) weißt du aber schon, dass ersteres nicht stimmt, da $x = 8$ und $y = 4$ eine Lösung ist. Deswegen hat das Gleichungssystem genau eine Lösung.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9
Ein Hotel verfügt über 105 Betten, die sich in 40 Zwei-bzw.-Dreibettzimmern befinden. Wie viele Zwei-und-Dreibettzimmer kann das Hotel vermieten?
Löse mit einem Gleichungssystem!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Gleichungen aus dem Text aufstellen
Was ist bekannt? Die Summe der Anzahl der Zweibettzimmer $x$ und der Anzahl der Dreibettzimmer $y$ beträgt 40. Diese Aussage liefert dir Gleichung $\mathrm{I}$ :
In einem Zweibettzimmer stehen zwei Betten. In $x$ Zweibettzimmern stehen somit $2\cdot x$ Betten und entsprechend stehen in den Dreibettzimmern $3\cdot x$ Betten. Insgesamt hat das Hotel 105 Betten, so dass du Gleichung $\mathrm{II}$ aufstellen kannst:
Du hast nun folgendes lineare Gleichungssystem mit zwei Gleichungen und zwei Unbekannten erhalten:
Gleichungssystem lösen
Zur Lösung dieses Gleichungssystems stehen dir drei Lösungsverfahren zur Verfügung:
Einsetzungsverfahren
Gleichsetzungsverfahren
Additionsverfahren
Lösung mit dem Einsetzungsverfahren
Löse Gleichung $\mathrm{I}$ nach einer der beiden Variablen auf und setze diese Variable in Gleichung $\mathrm{II}$ ein. Es spielt keine Rolle, ob du $\mathrm{I}$ nach $x$ oder $y$ auflöst.
$\mathrm{I'}\quad y=40-x$ . Eingesetzt in $\mathrm{II}:$
Setze $x=15$ in Gleichung $\mathrm{I'}$ ein: $y=40-15=25$
Die Lösungsmenge deines Gleichungssystems lautet also : $\mathbb{L}=\{(15\vert 25)\}$
Antwort: Das Hotel verfügt über $15$ Zweibettzimmer und über $25$ Dreibettzimmer.
Lösung mit dem Gleichsetzungsverfahren
Löse beide Gleichungen nach derselben Variablen auf. Du hast beim Einsetzungsverfahren schon Gleichung $\mathrm{I}$ nach $y$ aufgelöst.
$\mathrm{I'}\quad y=40-x$ . Nun muss Gleichung $\mathrm{II}$ auch nach $y$ aufgelöst werden:
Setze nun die beiden rechten Seiten der Gleichungen $\mathrm{I'}$ und $\mathrm{II'}$ gleich:
Setze $x=15$ in Gleichung $\mathrm{I'}$ ein: $y=40-15=25$
Die Lösungsmenge deines Gleichungssystems lautet also : $\mathbb{L}=\{(15\vert 25)\}$
Antwort: Das Hotel verfügt über $15$ Zweibettzimmer und über $25$ Dreibettzimmer.
Lösung mit dem Additionsverfahren
Ziel ist es, dass sich durch Addition der beiden Gleichungen eine der unbekannten Größen aufhebt. In diesem Gleichungssystem kannst du z.B. die Gleichung $\mathrm{I}$ mit $(-2)$ multiplizieren $\Rightarrow \mathrm{I'}$ . Durch Addition der beiden Gleichungen $\mathrm{I'}$ und $\mathrm{II}$ erhältst du schon die Lösung für $y$ :
Setze $y=25$ in Gleichung $\mathrm{I}$ ein: $x+25=40\Rightarrow x=15$
Die Lösungsmenge deines Gleichungssystems lautet also : $\mathbb{L}=\{(15\vert 25)\}$
Antwort: Das Hotel verfügt über $15$ Zweibettzimmer und über $25$ Dreibettzimmer.
Erstelle aus dem Aufgabentext ein lineares Gleichungssystem.
Tipp: Wähle die Variable $x$ für die Anzahl der Zweibettzimmer und die Variable $y$ für die Anzahl der Dreibettzimmer.
10
Ein Hotel verfügt über 105 Betten, die sich in 40 Zwei-bzw.-Dreibettzimmern befinden. Wie viele Zwei-und-Dreibettzimmer kann das Hotel vermieten?
Löse mit einem Gleichungssystem!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Gleichungen aus dem Text aufstellen
Was ist bekannt? Die Summe der Anzahl der Zweibettzimmer $x$ und der Anzahl der Dreibettzimmer $y$ beträgt 40. Diese Aussage liefert dir Gleichung $\mathrm{I}$ :
In einem Zweibettzimmer stehen zwei Betten. In $x$ Zweibettzimmern stehen somit $2\cdot x$ Betten und entsprechend stehen in den Dreibettzimmern $3\cdot x$ Betten. Insgesamt hat das Hotel 105 Betten, so dass du Gleichung $\mathrm{II}$ aufstellen kannst:
Du hast nun folgendes lineare Gleichungssystem mit zwei Gleichungen und zwei Unbekannten erhalten:
Gleichungssystem lösen
Zur Lösung dieses Gleichungssystems stehen dir drei Lösungsverfahren zur Verfügung:
Einsetzungsverfahren
Gleichsetzungsverfahren
Additionsverfahren
Lösung mit dem Einsetzungsverfahren
Löse Gleichung $\mathrm{I}$ nach einer der beiden Variablen auf und setze diese Variable in Gleichung $\mathrm{II}$ ein. Es spielt keine Rolle, ob du $\mathrm{I}$ nach $x$ oder $y$ auflöst.
$\mathrm{I'}\quad y=40-x$ . Eingesetzt in $\mathrm{II}:$
Setze $x=15$ in Gleichung $\mathrm{I'}$ ein: $y=40-15=25$
Die Lösungsmenge deines Gleichungssystems lautet also : $\mathbb{L}=\{(15\vert 25)\}$
Antwort: Das Hotel verfügt über $15$ Zweibettzimmer und über $25$ Dreibettzimmer.
Lösung mit dem Gleichsetzungsverfahren
Löse beide Gleichungen nach derselben Variablen auf. Du hast beim Einsetzungsverfahren schon Gleichung $\mathrm{I}$ nach $y$ aufgelöst.
$\mathrm{I'}\quad y=40-x$ . Nun muss Gleichung $\mathrm{II}$ auch nach $y$ aufgelöst werden:
Setze nun die beiden rechten Seiten der Gleichungen $\mathrm{I'}$ und $\mathrm{II'}$ gleich:
Setze $x=15$ in Gleichung $\mathrm{I'}$ ein: $y=40-15=25$
Die Lösungsmenge deines Gleichungssystems lautet also : $\mathbb{L}=\{(15\vert 25)\}$
Antwort: Das Hotel verfügt über $15$ Zweibettzimmer und über $25$ Dreibettzimmer.
Lösung mit dem Additionsverfahren
Ziel ist es, dass sich durch Addition der beiden Gleichungen eine der unbekannten Größen aufhebt. In diesem Gleichungssystem kannst du z.B. die Gleichung $\mathrm{I}$ mit $(-2)$ multiplizieren $\Rightarrow \mathrm{I'}$ . Durch Addition der beiden Gleichungen $\mathrm{I'}$ und $\mathrm{II}$ erhältst du schon die Lösung für $y$ :
Setze $y=25$ in Gleichung $\mathrm{I}$ ein: $x+25=40\Rightarrow x=15$
Die Lösungsmenge deines Gleichungssystems lautet also : $\mathbb{L}=\{(15\vert 25)\}$
Antwort: Das Hotel verfügt über $15$ Zweibettzimmer und über $25$ Dreibettzimmer.
Erstelle aus dem Aufgabentext ein lineares Gleichungssystem.
Tipp: Wähle die Variable $x$ für die Anzahl der Zweibettzimmer und die Variable $y$ für die Anzahl der Dreibettzimmer.
11
Ein Bauer hält in seinem Stall Hühner und Kaninchen. Er zählt insgesamt 120 Beine. Es gibt dreimal mehr Hühner als Kaninchen. Wie viele Hühner und Kaninchen hat der Bauer?
Löse mit einem Gleichungssystem!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Gleichungen aus dem Text aufstellen
Die Anzahl der Hühner bezeichnest du mit der Variablen $x$ und mit der Variablen $y$ die Anzahl der Kaninchen. Was ist bekannt? Ein Huhn hat zwei Beine, ein Kaninchen hat vier Beine. Somit haben $x$ Hühner $2\cdot x$ Beine und $y$ Kaninchen haben $4\cdot y$ Beine. Diese Aussage liefert dir Gleichung $\mathrm{I}$ :
"Es gibt dreimal mehr Hühner als Kaninchen" muss als Gleichung formuliert werden. Da $y$ die Anzahl der Kaninchen ist, musst du $y$ mit $3$ multiplizieren um die Anzahl $x$ der Hühner zu erhalten. Du kannst nun Gleichung $\mathrm{II}$ aufstellen:
Du hast nun folgendes lineare Gleichungssystem mit zwei Gleichungen und zwei Unbekannten erhalten:
Zur Lösung dieses Gleichungssystems stehen dir drei Lösungsverfahren zur Verfügung:
Einsetzungsverfahren
Gleichsetzungsverfahren
Additionsverfahren
Hier bietet sich das Einsetzungsverfahren an, da Gleichung $\mathrm{II}$ schon nach der Variablen $x$ aufgelöst ist.
Lösung mit dem Einsetzungsverfahren
Setze Gleichung $\mathrm{II}\;\; x =3\cdot y$ in Gleichung $\mathrm{I}$ ein:
$\def\arraystretch{1.25} \begin{array}{rcl}2\cdot (3y) +4y&=&120&\vert\text{Klammer auflösen}\\\\6y+4y&=&120&\vert\text{ zusammenfassen}\\\\10y&=&120&\vert:10\\\\y&=&12&\end{array}$
Setze $y=12$ in Gleichung $\mathrm{II}$ ein: $x=3 \cdot12=36$
Die Lösungsmenge deines Gleichungssystems lautet also : $\mathbb{L}=\{(36\vert 12)\}$
Antwort: Der Bauer besitzt $36$ Hühner und $12$ Kaninchen.
Erstelle aus dem Aufgabentext ein lineares Gleichungssystem.
Tipp: Wähle die Variable $x$ für die Anzahl der Hühner und die Variable $y$ für die Anzahl der Kaninchen.

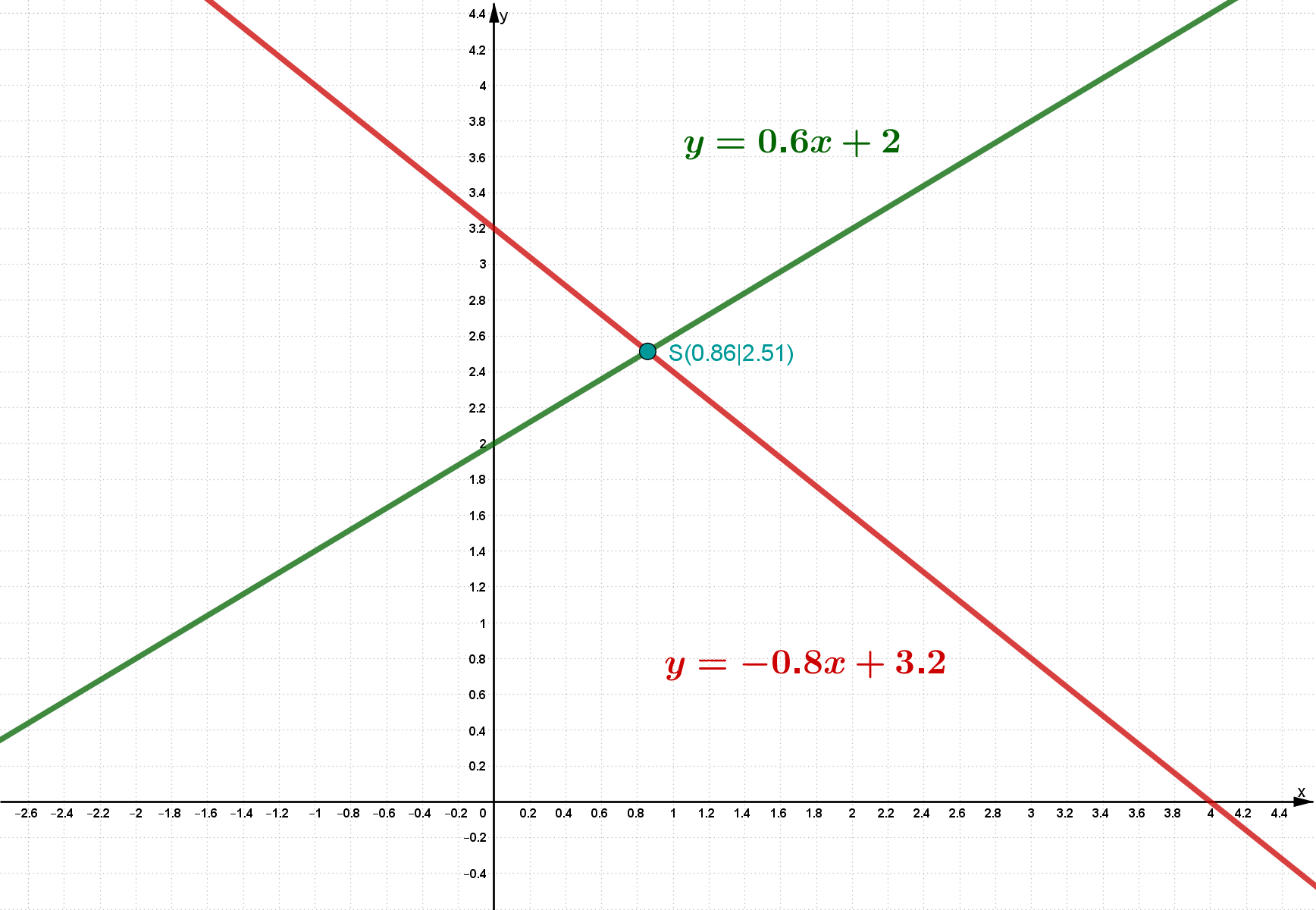
Gegeben ist das lineare Gleichungssystem

$\def\arraystretch{1.25} \begin{array}{cccccccc}\mathrm{(I)}&-x_1&+&2x_2&=&2\\\ \mathrm{(II)} \ &2x_1&-&x_2&=&2\end{array}$

Löse das System zunächst graphisch.

Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme
Löse Gleichung $\mathrm{(I)}$ nach $x_2$ auf:
$x_2=\dfrac{1}{2}\cdot x_1+1$
Die Gerade hat die Steigung $m=\frac{1}{2}$ und den $x_2$ -Achsenabschnitt $1$ .
Zeichne die Gerade ein.
In der Abbildung ist es die $\textcolor{660099}{\text{violette}}$ Gerade.
Löse Gleichung $\mathrm{(II)}$ nach $x_2$ auf:
$x_2=2\cdot x_1-2$
Die Gerade hat die Steigung $m=2$ und den $x_2$ -Achsenabschnitt $-2$ .
Zeichne die Gerade ein.
In der Abbildung ist es die $\textcolor{cc0000}{\text{rote}}$ Gerade.
Die beiden Geraden schneiden sich im Punkt $S(2|2)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Bestimme die Lösung des linearen Gleichungssystems mit einem Verfahren deiner Wahl.

Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Gleichungssysteme

Lösung mit dem Gleichsetzungsverfahren

Bei der Lösung zu $1$ hast du die beiden Gleichungen $x_2=\dfrac{1}{2}\cdot x_1+1$ und $x_2=2\cdot x_1-2$ erhalten. Die rechten Seiten können einander gleichgesetzt werden.

$\displaystyle \frac{1}{2}\cdot x_1+1$	$=$	$\displaystyle 2\cdot x_1-2$	$\displaystyle +2$
	↓	Löse nach $x_1$ auf.
$\displaystyle \frac{1}{2}\cdot x_1+3$	$=$	$\displaystyle 2\cdot x_1$	$\displaystyle -\frac{1}{2}\cdot x_1$
$\displaystyle 3$	$=$	$\displaystyle \frac{3}{2}\cdot x_1$	$\displaystyle \cdot\frac{2}{3}$
$\displaystyle 2$	$=$	$\displaystyle x_1$

Setze $x_1 =2$ in eine der beiden Gleichungen ein und berechne $x_2$ .

$x_2=\dfrac{1}{2}\cdot x_1+1 \;\Rightarrow\;x_2=\dfrac{1}{2}\cdot 2+1 =2$

Ergebnis: Das Gleichungssystem hat die Lösung $\mathbb{L}=\{(2|2)\}$ .

Lösung mit dem Einsetzungsverfahren

Bei der Lösung zu $1$ hast du die Gleichung $x_2=\dfrac{1}{2}\cdot x_1+1$ erhalten. Setze $x_2$ in Gleichung $\mathrm{(II)}$ ein:

$\displaystyle 2\cdot x_1-x_2$	$=$	$\displaystyle 2$
	↓	Setze $x_2=\dfrac{1}{2}\cdot x_1+1$ ein.
$\displaystyle 2\cdot x_1-(\frac{1}{2}\cdot x_1+1)$	$=$	$\displaystyle 2$
	↓	Löse die Klammer auf.
$\displaystyle 2\cdot x_1-\frac{1}{2}\cdot x_1-1$	$=$	$\displaystyle 2$	$\displaystyle +1$
	↓	Löse nach $x_1$ auf.
$\displaystyle \frac{3}{2}\cdot x_1$	$=$	$\displaystyle 3$	$\displaystyle \cdot\frac{2}{3}$
$\displaystyle x_1$	$=$	$\displaystyle 2$

Setze $x_1 =2$ in eine der beiden Gleichungen ein und berechne $x_2$ .

$x_2=\dfrac{1}{2}\cdot x_1+1 \;\Rightarrow\;x_2=\dfrac{1}{2}\cdot 2+1 =2$

Ergebnis: Das Gleichungssystem hat die Lösung $\mathbb{L}=\{(2|2)\}$ .

Lösung mit dem Additionsverfahren

$\def\arraystretch{1.25} \begin{array}{cccccccc}\mathrm{(I)}&-x_1&+&2x_2&=&2\\\ \mathrm{(II)} \ &2x_1&-&x_2&=&2\end{array}$

Beseitige z.B. die Variable $x_1$ , indem du rechnest: $2 \cdot \mathrm{(I)} +\mathrm{(II)}$

$\Rightarrow\;4x_2-x_2=4+2\;\Rightarrow\;3x_2=6\;\Rightarrow\;x_2=2$

Setze den berechneten Wert $x_2=2$ z.B. in Gleichung $\mathrm{(II)}$ ein:

$\Rightarrow\;2x_1-2=2\;\Rightarrow\;2x_1=4\;\Rightarrow\;x_1=2$

Ergebnis: Das Gleichungssystem hat die Lösung $\mathbb{L}=\{(2|2)\}$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \text{I}\ \ \ \ \ \ 3\cdot\left(-\frac{7}{9}\right)+4$	$=$	$\displaystyle y$
$\displaystyle \frac{3\cdot\left(-7\right)}{9}+4$	$=$	$\displaystyle y$
$\displaystyle \frac{3\cdot\left(-7\right)}{3\cdot3}+4$	$=$	$\displaystyle y$
	↓	Kürze den linken Bruch mit 3 und schreibe 4 als Bruch.
$\displaystyle -\frac{7}{3}+\frac{4}{1}$	$=$	$\displaystyle y$
	↓	Erweitere $\frac 41$ mit 3, um die Brüche zu addieren.
$\displaystyle -\frac{7}{3}+\frac{4\cdot3}{1\cdot3}$	$=$	$\displaystyle y$
	↓	Addiere die Brüche
$\displaystyle \frac{\left(-7\right)+12}{3}$	$=$	$\displaystyle y$
$\displaystyle \frac{5}{3}$	$=$	$\displaystyle y$

$\displaystyle v-s$	$=$	$\displaystyle 26$
	↓	Nach $v$ auflösen.
$\displaystyle v$	$=$	$\displaystyle s+26$
	↓	In die obere Gleichung einsetzen.
$\displaystyle 26+2s$	$=$	$\displaystyle 34$
	↓	Nach $s$ auflösen.
$\displaystyle 2s$	$=$	$\displaystyle 8$
$\displaystyle s$	$=$	$\displaystyle 4$

$\displaystyle I\ x+y$	$=$	$\displaystyle 5$	$\displaystyle -x$
$\displaystyle I´\ y$	$=$	$\displaystyle 5-x$
$\displaystyle II\ 1{,}35\cdot x+1{,}2\cdot y$	$=$	$\displaystyle 6{,}5$	$\displaystyle -1{,}35\cdot x$
$\displaystyle II\ 1{,}2\cdot y$	$=$	$\displaystyle 6{,}5-1{,}35\cdot x$	$\displaystyle :1{,}2$
$\displaystyle II´y$	$=$	$\displaystyle \frac{65}{12}-1{,}125\cdot x$

$\displaystyle 5-x$	$=$	$\displaystyle \frac{65}{12}-1{,}125\cdot x$	$\displaystyle +1{,}125⋅x\ −5$
$\displaystyle 0{,}125\cdot x$	$=$	$\displaystyle \frac{5}{12}$	$\displaystyle :0{,}125$
$\displaystyle x$	$=$	$\displaystyle \frac{10}{3}$

Aufgaben zum Lösen linearer Gleichungssysteme

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lineares Gleichungssystem mit zwei Unbekannten

Graphisches Lösen

Rechnerisches Lösen

Hast du eine Frage oder Feedback?

Lineares Gleichungssystem mit zwei Unbekannten

Graphisches Lösen

Rechnerisches Lösen

Hast du eine Frage oder Feedback?

Lineares Gleichungssystem mit zwei Unbekannten

Graphisches Lösen

Rechnerisches Lösen

Hast du eine Frage oder Feedback?

Gleichungen aus dem Text aufstellen

Einsetzungsverfahren

1. Schritt: Löse nach einer Variablen auf

2. Schritt: Setze mmm in I\mathrm{I}I ein

3. Schritt: Setze jjj in II\mathrm{II}II ein

Lösungsmenge bestimmen

Suche dir Variablen aus und stelle die Gleichungen auf

Additions-/Subtraktionsverfahren

Nach der ersten Variablen auflösen

Setze xxx in I\mathrm{I}I oder II\mathrm{II}II ein

Lösungsmenge

Lösung im Sachkontext

Blaue Kerze

Rote Kerze

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Höhe der Kerzen

Was bedeutet das −2,75\color{red}{-}2{,}75−2,75 cm?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Gleichungen aus dem Text aufstellen

Gleichungssystem lösen

Lösung mit dem Einsetzungsverfahren

Lösung mit dem Gleichsetzungsverfahren

Lösung mit dem Additionsverfahren

Gleichungen aus dem Text aufstellen

Gleichungssystem lösen

Lösung mit dem Einsetzungsverfahren

Lösung mit dem Gleichsetzungsverfahren

Lösung mit dem Additionsverfahren

Gleichungen aus dem Text aufstellen

Lösung mit dem Einsetzungsverfahren

Hast du eine Frage oder Feedback?

Lösung mit dem Gleichsetzungsverfahren

Bei der Lösung zu 111 hast du die beiden Gleichungen x2=12⋅x1+1x_2=\dfrac{1}{2}\cdot x_1+1 x2​=21​⋅x1​+1 und x2=2⋅x1−2x_2=2\cdot x_1-2 x2​=2⋅x1​−2 erhalten. Die rechten Seiten können einander gleichgesetzt werden.

Lösung mit dem Einsetzungsverfahren

Bei der Lösung zu 111 hast du die Gleichung x2=12⋅x1+1x_2=\dfrac{1}{2}\cdot x_1+1 x2​=21​⋅x1​+1 erhalten. Setze x2x_2x2​ in Gleichung (II)\mathrm{(II)}(II) ein:

Lösung mit dem Additionsverfahren

Hast du eine Frage oder Feedback?

2. Schritt: Setze $m$ in $\mathrm{I}$ ein

3. Schritt: Setze $j$ in $\mathrm{II}$ ein

Setze $x$ in $\mathrm{I}$ oder $\mathrm{II}$ ein

Was bedeutet das $\color{red}{-}2{,}75$ cm?

Bei der Lösung zu $1$ hast du die beiden Gleichungen $x_2=\dfrac{1}{2}\cdot x_1+1$ und $x_2=2\cdot x_1-2$ erhalten. Die rechten Seiten können einander gleichgesetzt werden.

Bei der Lösung zu $1$ hast du die Gleichung $x_2=\dfrac{1}{2}\cdot x_1+1$ erhalten. Setze $x_2$ in Gleichung $\mathrm{(II)}$ ein: